19 results in 26Cxx
Absolute concentration robustness and multistationarity in reaction networks: Conditions for coexistence
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 02 January 2024, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The blowup-polynomial of a metric space: connections to stable polynomials, graphs and their distance spectra
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 November 2023, pp. 1-42
-
- Article
- Export citation
Approximation and homotopy in regulous geometry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 November 2023, pp. 1-20
- Print publication:
- January 2024
-
- Article
- Export citation
ON THE NUMBER OF REAL ZEROS OF POLYNOMIALS OF EVEN DEGREE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 89-93
- Print publication:
- February 2024
-
- Article
- Export citation
Some analytical properties of the matrix related to q-coloured Delannoy numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 06 October 2022, pp. 847-860
-
- Article
- Export citation
Step roots of Littlewood polynomials and the extrema of functions in the Takagi class
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 591-618
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hilbert’s 17th problem in free skew fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 06 September 2021, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting matchings via capacity-preserving operators
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 956-981
-
- Article
-
- You have access
- Open access
- Export citation
STRICTLY REAL FUNDAMENTAL THEOREM OF ALGEBRA USING POLYNOMIAL INTERLACING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 18 January 2021, pp. 249-255
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
ALGEBRAIC STRUCTURE OF THE RANGE OF A TRIGONOMETRIC POLYNOMIAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 251-260
- Print publication:
- October 2020
-
- Article
- Export citation
A STABILITY VERSION OF THE GAUSS–LUCAS THEOREM AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 05 September 2019, pp. 262-269
- Print publication:
- October 2020
-
- Article
- Export citation
Persistence probability of a random polynomial arising from evolutionary game theory
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 870-890
- Print publication:
- September 2019
-
- Article
- Export citation
Interlacing polynomials and the veronese construction for rational formal power series
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1-16
- Print publication:
- February 2020
-
- Article
- Export citation
ARITHMETIC ASPECTS OF SYMMETRIC EDGE POLYTOPES
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 14 May 2019, pp. 763-784
- Print publication:
- 2019
-
- Article
- Export citation
THE LOCAL
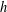 $h$-POLYNOMIALS OF CLUSTER SUBDIVISIONS HAVE ONLY REAL ZEROS
$h$-POLYNOMIALS OF CLUSTER SUBDIVISIONS HAVE ONLY REAL ZEROS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 258-264
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
NEIGHBORLINESS OF THE SYMMETRIC MOMENT CURVE
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 12 April 2012, pp. 223-249
- Print publication:
- January 2013
-
- Article
- Export citation
A GENERALISATION OF DESCARTES’ RULE OF SIGNS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 24 January 2012, pp. 415-420
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
The zeros of linear combinations of translates of polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 109-118
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
Bounds for the separations of real zeros of polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 3 / December 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 330-342
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation



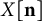
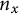
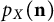
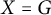

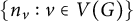
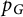
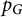
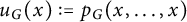
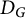
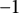
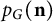
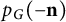
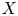
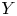
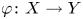
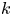
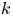
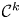
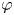
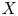
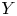
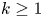
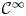
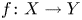
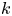
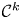
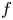
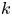

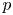
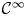
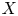
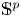
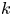
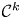
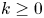
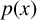

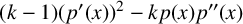
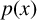
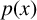
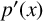
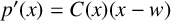
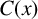
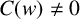
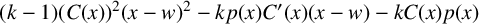
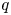
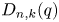
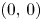
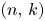
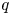
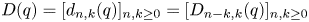
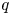
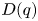
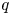
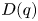
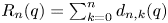
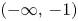
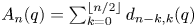
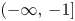
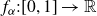
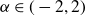
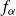
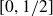
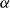
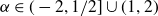
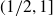
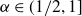
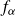
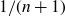
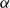
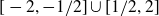
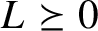
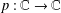
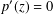
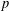
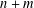

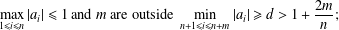
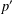
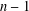

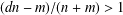


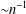
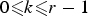
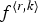
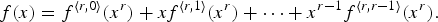
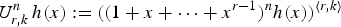
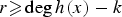
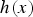
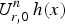
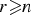
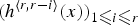
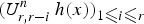
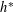

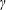
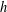
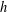
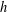
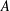
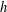
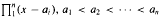 by δ(
by δ(