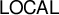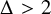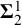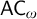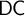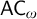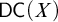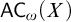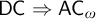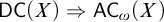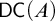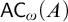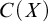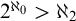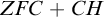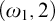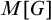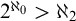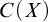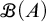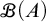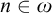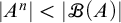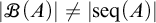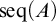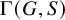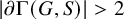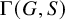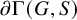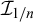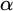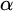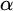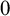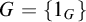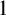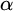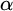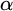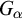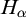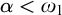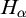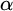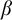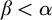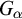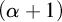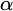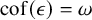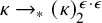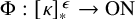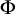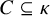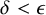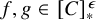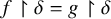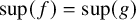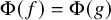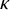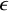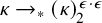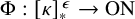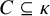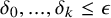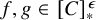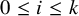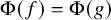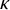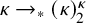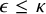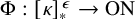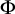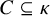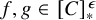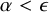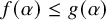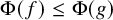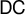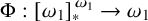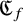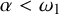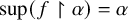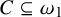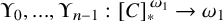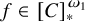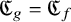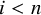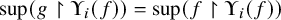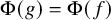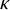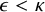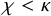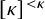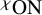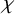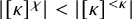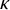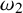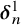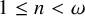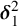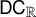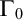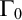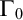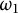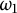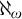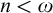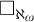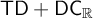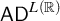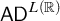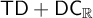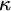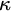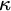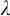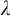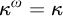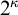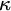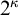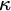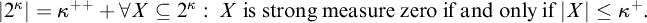282 results in 03EXX
ON HOMOMORPHISM GRAPHS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 May 2024, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distributivity and base trees for
 $P(\kappa)/ {\lt} \kappa$
$P(\kappa)/ {\lt} \kappa$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 07 May 2024, pp. 1-12
-
- Article
- Export citation
DOES
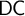 $\mathsf {DC}$ IMPLY
$\mathsf {DC}$ IMPLY 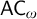 ${\mathsf {AC}}_\omega $, UNIFORMLY?
${\mathsf {AC}}_\omega $, UNIFORMLY?
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1-25
-
- Article
- Export citation
THE DEFINABILITY OF THE EXTENDER SEQUENCE
 $\mathbb {E}$ FROM
$\mathbb {E}$ FROM  $\mathbb {E}\upharpoonright \aleph _1$ IN
$\mathbb {E}\upharpoonright \aleph _1$ IN  $L[\mathbb {E}]$
$L[\mathbb {E}]$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 427-459
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DISCONTINUOUS HOMOMORPHISMS OF
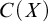 $C(X)$ WITH
$C(X)$ WITH 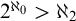 $2^{\aleph _0}>\aleph _2$
$2^{\aleph _0}>\aleph _2$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 665-696
- Print publication:
- June 2024
-
- Article
- Export citation
CANTOR’S THEOREM MAY FAIL FOR FINITARY PARTITIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 April 2024, pp. 1-18
-
- Article
- Export citation
WAND/SET THEORIES: A REALIZATION OF CONWAY’S MATHEMATICIANS’ LIBERATION MOVEMENT, WITH AN APPLICATION TO CHURCH’S SET THEORY WITH A UNIVERSAL SET
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 25 March 2024, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structural, point-free, non-Hausdorff topological realization of Borel groupoid actions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 14 March 2024, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWO-CARDINAL DERIVED TOPOLOGIES, INDESCRIBABILITY AND RAMSEYNESS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 March 2024, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hyperfiniteness of boundary actions of acylindrically hyperbolic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 March 2024, e32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A UNIFIED APPROACH TO HINDMAN, RAMSEY, AND VAN DER WAERDEN SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 February 2024, pp. 1-53
-
- Article
- Export citation
A HIERARCHY ON NON-ARCHIMEDEAN POLISH GROUPS ADMITTING A COMPATIBLE COMPLETE LEFT-INVARIANT METRIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 06 February 2024, pp. 1-19
-
- Article
- Export citation
Almost Everywhere Behavior of Functions According to Partition Measures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 29 January 2024, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POINCARÉ–WEYL’S PREDICATIVITY: GOING BEYOND
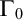 $\Gamma _{0}$
$\Gamma _{0}$
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 41-91
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POLISH SPACE PARTITION PRINCIPLES AND THE HALPERN–LÄUCHLI THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 19 January 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Borel reducibility of equivalence relations on
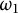 $\omega _1$
$\omega _1$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON COMPACTNESS OF WEAK SQUARE AT SINGULARS OF UNCOUNTABLE COFINALITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 04 January 2024, pp. 1-11
-
- Article
- Export citation
NOTE ON
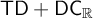 $\mathsf {TD} + \mathsf {DC}_{\mathbb {R}}$ IMPLYING
$\mathsf {TD} + \mathsf {DC}_{\mathbb {R}}$ IMPLYING 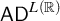 $\mathsf {AD}^{L(\mathbb {R})}$
$\mathsf {AD}^{L(\mathbb {R})}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 04 January 2024, pp. 211-217
- Print publication:
- March 2024
-
- Article
- Export citation
PARTITION OF LARGE SUBSETS OF SEMIGROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 January 2024, pp. 1-6
-
- Article
- Export citation
STRONG MEASURE ZERO SETS ON
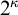 $2^\kappa $ FOR
$2^\kappa $ FOR 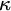 $\kappa $ INACCESSIBLE
$\kappa $ INACCESSIBLE
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 January 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation