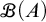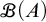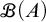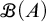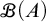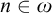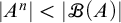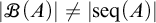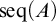1 Introduction
In 1891, Cantor [Reference Cantor1] proved that, for all sets A, there are no surjections from A onto
![]() $\mathscr {P}(A)$
(the power set of A). Under the axiom of choice, for infinite sets A, several sets related to A have the same cardinality as
$\mathscr {P}(A)$
(the power set of A). Under the axiom of choice, for infinite sets A, several sets related to A have the same cardinality as
![]() $\mathscr {P}(A)$
or A; for example,
$\mathscr {P}(A)$
or A; for example,
![]() $\mathcal {S}(A)$
(the set of all permutations of A) and
$\mathcal {S}(A)$
(the set of all permutations of A) and
![]() $\mathrm {Part}(A)$
(the set of all partitions of A) have the same cardinality as
$\mathrm {Part}(A)$
(the set of all partitions of A) have the same cardinality as
![]() $\mathscr {P}(A)$
, and
$\mathscr {P}(A)$
, and
![]() $A^2$
,
$A^2$
,
![]() $\mathrm {fin}(A)$
(the set of all finite subsets of A),
$\mathrm {fin}(A)$
(the set of all finite subsets of A),
![]() $\mathrm {seq}(A)$
(the set of all finite sequences of elements of A), and
$\mathrm {seq}(A)$
(the set of all finite sequences of elements of A), and
![]() $\mathrm {seq}^{\text {1-1}}(A)$
(the set of all finite sequences without repetition of elements of A) have the same cardinality as A. However, without the axiom of choice, this is no longer the case. In 1924, Tarski [Reference Tarski19] proved that the statement that
$\mathrm {seq}^{\text {1-1}}(A)$
(the set of all finite sequences without repetition of elements of A) have the same cardinality as A. However, without the axiom of choice, this is no longer the case. In 1924, Tarski [Reference Tarski19] proved that the statement that
![]() $A^2$
has the same cardinality as A for all infinite sets A is in fact equivalent to the axiom of choice.
$A^2$
has the same cardinality as A for all infinite sets A is in fact equivalent to the axiom of choice.
Over the past century, various variations of Cantor’s theorem have been investigated in
![]() $\mathsf {ZF}$
(the Zermelo–Fraenkel set theory without the axiom of choice), with A or
$\mathsf {ZF}$
(the Zermelo–Fraenkel set theory without the axiom of choice), with A or
![]() $\mathscr {P}(A)$
replaced by a set which has the same cardinality under the axiom of choice. Specker [Reference Specker18] proves that, for all infinite sets A, there are no injections from
$\mathscr {P}(A)$
replaced by a set which has the same cardinality under the axiom of choice. Specker [Reference Specker18] proves that, for all infinite sets A, there are no injections from
![]() $\mathscr {P}(A)$
into
$\mathscr {P}(A)$
into
![]() $A^2$
. Halbeisen and Shelah [Reference Halbeisen and Shelah5] prove that
$A^2$
. Halbeisen and Shelah [Reference Halbeisen and Shelah5] prove that
![]() $|\mathrm {fin}(A)|<|\mathscr {P}(A)|$
and
$|\mathrm {fin}(A)|<|\mathscr {P}(A)|$
and
![]() $|\mathrm {seq}^{\text {1-1}}(A)|\neq |\mathscr {P}(A)|\neq |\mathrm {seq}(A)|$
. Forster [Reference Forster3] proves that there are no finite-to-one functions from
$|\mathrm {seq}^{\text {1-1}}(A)|\neq |\mathscr {P}(A)|\neq |\mathrm {seq}(A)|$
. Forster [Reference Forster3] proves that there are no finite-to-one functions from
![]() $\mathscr {P}(A)$
to A. Recently, Peng and Shen [Reference Peng and Shen8] prove that there are no surjections from
$\mathscr {P}(A)$
to A. Recently, Peng and Shen [Reference Peng and Shen8] prove that there are no surjections from
![]() $\omega \times A$
onto
$\omega \times A$
onto
![]() $\mathscr {P}(A)$
, and Peng, Shen, and Wu [Reference Peng, Shen and Wu9] prove that the existence of an infinite set A and a surjection from
$\mathscr {P}(A)$
, and Peng, Shen, and Wu [Reference Peng, Shen and Wu9] prove that the existence of an infinite set A and a surjection from
![]() $A^2$
onto
$A^2$
onto
![]() $\mathscr {P}(A)$
is consistent with
$\mathscr {P}(A)$
is consistent with
![]() $\mathsf {ZF}$
. The variations of Cantor’s theorem with
$\mathsf {ZF}$
. The variations of Cantor’s theorem with
![]() $\mathscr {P}(A)$
replaced by
$\mathscr {P}(A)$
replaced by
![]() $\mathcal {S}(A)$
are investigated in [Reference Dawson and Howard2, Reference Shen and Yuan15–Reference Sonpanow and Vejjajiva17].
$\mathcal {S}(A)$
are investigated in [Reference Dawson and Howard2, Reference Shen and Yuan15–Reference Sonpanow and Vejjajiva17].
For a set A, let
![]() $\mathscr {B}(A)$
be the set of all finitary partitions of A, where a partition is finitary if all its members are finite. We use the symbol
$\mathscr {B}(A)$
be the set of all finitary partitions of A, where a partition is finitary if all its members are finite. We use the symbol
![]() $\mathscr {B}$
to denote this notion just because
$\mathscr {B}$
to denote this notion just because
![]() $|\mathscr {B}(n)|$
is the nth Bell number. The axiom of choice implies that
$|\mathscr {B}(n)|$
is the nth Bell number. The axiom of choice implies that
![]() $\mathscr {B}(A)$
and
$\mathscr {B}(A)$
and
![]() $\mathscr {P}(A)$
have the same cardinality for infinite sets A, but each of “
$\mathscr {P}(A)$
have the same cardinality for infinite sets A, but each of “
![]() $|\mathscr {B}(A)|<|\mathscr {P}(A)|$
”, “
$|\mathscr {B}(A)|<|\mathscr {P}(A)|$
”, “
![]() $|\mathscr {P}(A)|<|\mathscr {B}(A)|$
”, and “
$|\mathscr {P}(A)|<|\mathscr {B}(A)|$
”, and “
![]() $|\mathscr {B}(A)|$
and
$|\mathscr {B}(A)|$
and
![]() $|\mathscr {P}(A)|$
are incomparable” for some infinite set A is consistent with
$|\mathscr {P}(A)|$
are incomparable” for some infinite set A is consistent with
![]() $\mathsf {ZF}$
. Recently, Phansamdaeng and Vejjajiva [Reference Phansamdaeng and Vejjajiva10] prove that
$\mathsf {ZF}$
. Recently, Phansamdaeng and Vejjajiva [Reference Phansamdaeng and Vejjajiva10] prove that
![]() $|\mathrm {fin}(A)|<|\mathscr {B}(A)|$
for all infinite sets A.
$|\mathrm {fin}(A)|<|\mathscr {B}(A)|$
for all infinite sets A.
In this paper, we further study the variations of Cantor’s theorem with
![]() $\mathscr {P}(A)$
replaced by
$\mathscr {P}(A)$
replaced by
![]() $\mathscr {B}(A)$
. We show that Cantor’s theorem may fail for finitary partitions in the sense that the existence of an infinite set A and a surjection from A onto
$\mathscr {B}(A)$
. We show that Cantor’s theorem may fail for finitary partitions in the sense that the existence of an infinite set A and a surjection from A onto
![]() $\mathscr {B}(A)$
is consistent with
$\mathscr {B}(A)$
is consistent with
![]() $\mathsf {ZF}$
. Nevertheless, we prove in
$\mathsf {ZF}$
. Nevertheless, we prove in
![]() $\mathsf {ZF}$
some theorems concerning
$\mathsf {ZF}$
some theorems concerning
![]() $\mathscr {B}(A)$
for infinite sets A, among which are the following:
$\mathscr {B}(A)$
for infinite sets A, among which are the following:
-
(1) If there is a finitary partition of A without singleton blocks, then there are no surjections from A onto
 $\mathscr {B}(A)$
and no finite-to-one functions from
$\mathscr {B}(A)$
and no finite-to-one functions from
 $\mathscr {B}(A)$
to A.
$\mathscr {B}(A)$
to A. -
(2) For all
 $n\in \omega $
,
$n\in \omega $
,
 $|A^n|<|\mathscr {B}(A)|$
.
$|A^n|<|\mathscr {B}(A)|$
. -
(3)
 $|\mathscr {B}(A)|\neq |\mathrm {seq}(A)|$
.
$|\mathscr {B}(A)|\neq |\mathrm {seq}(A)|$
.
2 Some notation and preliminary results
Throughout this paper, we shall work in
![]() $\mathsf {ZF}$
. In this section, we indicate briefly our use of some terminology and notation. For a function f, we use
$\mathsf {ZF}$
. In this section, we indicate briefly our use of some terminology and notation. For a function f, we use
![]() ${\operatorname {dom}}(f)$
for the domain of f,
${\operatorname {dom}}(f)$
for the domain of f,
![]() ${\operatorname {ran}}(f)$
for the range of f,
${\operatorname {ran}}(f)$
for the range of f,
![]() $f[A]$
for the image of A under f,
$f[A]$
for the image of A under f,
![]() $f^{-1}[A]$
for the inverse image of A under f, and
$f^{-1}[A]$
for the inverse image of A under f, and
![]() $f{\upharpoonright } A$
for the restriction of f to A. For functions f and g, we use
$f{\upharpoonright } A$
for the restriction of f to A. For functions f and g, we use
![]() $g\circ f$
for the composition of g and f. We write
$g\circ f$
for the composition of g and f. We write
![]() $f:A\to B$
to express that f is a function from A to B, and
$f:A\to B$
to express that f is a function from A to B, and
![]() $f:A\twoheadrightarrow B$
to express that f is a function from A onto B. For a set A,
$f:A\twoheadrightarrow B$
to express that f is a function from A onto B. For a set A,
![]() $|A|$
denotes the cardinality of A.
$|A|$
denotes the cardinality of A.
Definition 2.1. Let
![]() $A,B$
be arbitrary sets.
$A,B$
be arbitrary sets.
-
(1)
 $|A|=|B|$
, or
$|A|=|B|$
, or
 $A\approx B$
, if there is a bijection between A and B.
$A\approx B$
, if there is a bijection between A and B. -
(2)
 $|A|\leqslant |B|$
, or
$|A|\leqslant |B|$
, or
 $A\preccurlyeq B$
, if there is an injection from A into B.
$A\preccurlyeq B$
, if there is an injection from A into B. -
(3)
 $|A|\leqslant ^\ast |B|$
, or
$|A|\leqslant ^\ast |B|$
, or
 $A\preccurlyeq ^\ast B$
, if there is a surjection from a subset of B onto A.
$A\preccurlyeq ^\ast B$
, if there is a surjection from a subset of B onto A. -
(4)
 $|A|<|B|$
if
$|A|<|B|$
if
 $|A|\leqslant |B|$
and
$|A|\leqslant |B|$
and
 $|A|\neq |B|$
.
$|A|\neq |B|$
.
Clearly, if
![]() $A\preccurlyeq B$
then
$A\preccurlyeq B$
then
![]() $A\preccurlyeq ^\ast B$
, and if
$A\preccurlyeq ^\ast B$
, and if
![]() $A\preccurlyeq ^\ast B$
then
$A\preccurlyeq ^\ast B$
then
![]() $\mathscr {P}(A)\preccurlyeq \mathscr {P}(B)$
.
$\mathscr {P}(A)\preccurlyeq \mathscr {P}(B)$
.
In the sequel, we shall frequently use expressions like “one can explicitly define” in our formulations, which is illustrated by the following example.
Theorem 2.2 (Cantor–Bernstein).
From injections
![]() $f:A\to B$
and
$f:A\to B$
and
![]() $g:B\to A$
, one can explicitly define a bijection
$g:B\to A$
, one can explicitly define a bijection
![]() $h:A\to B$
.
$h:A\to B$
.
Proof See [Reference Halbeisen4, Theorem 3.14].
Formally, Theorem 2.2 states that one can define a class function H without free variables such that, whenever f is an injection from A into B and g is an injection from B into A,
![]() $H(f,g)$
is defined and is a bijection between A and B. Consequently, if
$H(f,g)$
is defined and is a bijection between A and B. Consequently, if
![]() $|A|\leqslant |B|$
and
$|A|\leqslant |B|$
and
![]() $|B|\leqslant |A|$
, then
$|B|\leqslant |A|$
, then
![]() $|A|=|B|$
.
$|A|=|B|$
.
Definition 2.3. Let A be a set and let f be a function.
-
(1) A is Dedekind infinite if
 $\omega \preccurlyeq A$
; otherwise, A is Dedekind finite.
$\omega \preccurlyeq A$
; otherwise, A is Dedekind finite. -
(2) A is power Dedekind infinite if
 $\mathscr {P}(A)$
is Dedekind infinite; otherwise, A is power Dedekind finite.
$\mathscr {P}(A)$
is Dedekind infinite; otherwise, A is power Dedekind finite. -
(3) f is (Dedekind) finite-to-one if for every
 $z\in {\operatorname {ran}}(f)$
,
$z\in {\operatorname {ran}}(f)$
,
 $f^{-1}[\{z\}]$
is (Dedekind) finite.
$f^{-1}[\{z\}]$
is (Dedekind) finite.
Clearly, if f and g are (Dedekind) finite-to-one functions, so is
![]() $g\circ f$
(cf. [Reference Shen12, Fact 2.8]). It is well known that A is Dedekind infinite if and only if there exists a bijection between A and a proper subset of A. For power Dedekind infinite sets, recall Kuratowski’s celebrated theorem.
$g\circ f$
(cf. [Reference Shen12, Fact 2.8]). It is well known that A is Dedekind infinite if and only if there exists a bijection between A and a proper subset of A. For power Dedekind infinite sets, recall Kuratowski’s celebrated theorem.
Theorem 2.4 (Kuratowski).
A is power Dedekind infinite if and only if
![]() $\omega \preccurlyeq ^\ast A$
.
$\omega \preccurlyeq ^\ast A$
.
Proof See [Reference Halbeisen4, Proposition 5.4].
The following two facts are Corollaries 2.9 and 2.11 of [Reference Shen12], respectively.
Fact 2.5. If A is power Dedekind infinite and there exists a finite-to-one function from A to B, then B is power Dedekind infinite.
Fact 2.6. If
![]() $A^n$
is power Dedekind infinite, so is A.
$A^n$
is power Dedekind infinite, so is A.
Definition 2.7. Let P be a partition of A. We say that P is finitary if all blocks of P are finite, and write
![]() ${\operatorname {ns}}(P)$
for the set of non-singleton blocks of P. For
${\operatorname {ns}}(P)$
for the set of non-singleton blocks of P. For
![]() $x\in A$
, we write
$x\in A$
, we write
![]() $[x]_P$
for the unique block of P which contains x. The equivalence relation
$[x]_P$
for the unique block of P which contains x. The equivalence relation
![]() $\sim _P$
on A induced by P is defined by
$\sim _P$
on A induced by P is defined by
Definition 2.8. Let A be an arbitrary set.
-
(1)
 ${\operatorname {Part}}(A)$
is the set of all partitions of A.
${\operatorname {Part}}(A)$
is the set of all partitions of A. -
(2)
 ${\operatorname {Part}_{\operatorname {fin}}}(A)=\{P\in {\operatorname {Part}}(A)\mid P\text { is finite}\}$
.
${\operatorname {Part}_{\operatorname {fin}}}(A)=\{P\in {\operatorname {Part}}(A)\mid P\text { is finite}\}$
. -
(3)
 $\mathscr {B}(A)=\{P\in {\operatorname {Part}}(A)\mid P\text { is finitary}\}$
.
$\mathscr {B}(A)=\{P\in {\operatorname {Part}}(A)\mid P\text { is finitary}\}$
. -
(4)
 ${\mathscr {B}_{\operatorname {fin}}}(A)=\{P\in \mathscr {B}(A)\mid {\operatorname {ns}}(P)\text { is finite}\}$
.
${\mathscr {B}_{\operatorname {fin}}}(A)=\{P\in \mathscr {B}(A)\mid {\operatorname {ns}}(P)\text { is finite}\}$
. -
(5)
 $\operatorname {fin}(A)$
is the set of all finite subsets of A.
$\operatorname {fin}(A)$
is the set of all finite subsets of A. -
(6)
 ${\operatorname {seq}}(A)=\{f\mid f\text { is a function from an }n\in \omega \text { to }A\}$
.
${\operatorname {seq}}(A)=\{f\mid f\text { is a function from an }n\in \omega \text { to }A\}$
. -
(7)
 ${\operatorname {seq}^{1-1}}(A)=\{f\mid f\text { is an injection from an }n\in \omega \text { into }A\}$
.
${\operatorname {seq}^{1-1}}(A)=\{f\mid f\text { is an injection from an }n\in \omega \text { into }A\}$
.
Below we list some basic relations between the cardinalities of these sets. We first note that
![]() $\operatorname {fin}(A)\preccurlyeq ^\ast {\operatorname {seq}^{1-1}}(A)\preccurlyeq {\operatorname {seq}}(A)$
. The next three facts are Facts 2.13, 2.16, and 2.17 of [Reference Shen12], respectively.
$\operatorname {fin}(A)\preccurlyeq ^\ast {\operatorname {seq}^{1-1}}(A)\preccurlyeq {\operatorname {seq}}(A)$
. The next three facts are Facts 2.13, 2.16, and 2.17 of [Reference Shen12], respectively.
Fact 2.9. If A is infinite, then
![]() $\operatorname {fin}(A)$
and
$\operatorname {fin}(A)$
and
![]() $\mathscr {P}(A)$
are power Dedekind infinite.
$\mathscr {P}(A)$
are power Dedekind infinite.
Fact 2.10.
![]() ${\operatorname {seq}^{1-1}}(A)\preccurlyeq \operatorname {fin}(\operatorname {fin}(A))$
.
${\operatorname {seq}^{1-1}}(A)\preccurlyeq \operatorname {fin}(\operatorname {fin}(A))$
.
Fact 2.11. There is a finite-to-one function from
![]() $\operatorname {fin}(\operatorname {fin}(A))$
to
$\operatorname {fin}(\operatorname {fin}(A))$
to
![]() $\operatorname {fin}(A)$
.
$\operatorname {fin}(A)$
.
The next three facts are Facts 2.19, 2.20, and Corollary 2.23 of [Reference Shen and Yuan15], respectively.
Fact 2.12. If A is non-empty, then
![]() ${\operatorname {seq}}(A)$
is Dedekind infinite.
${\operatorname {seq}}(A)$
is Dedekind infinite.
Fact 2.13. If A is Dedekind finite, then there is a Dedekind finite-to-one function from
![]() ${\operatorname {seq}}(A)$
to
${\operatorname {seq}}(A)$
to
![]() $\omega $
.
$\omega $
.
Fact 2.14. If A is Dedekind infinite, then
![]() ${\operatorname {seq}}(A)\approx {\operatorname {seq}^{1-1}}(A)$
.
${\operatorname {seq}}(A)\approx {\operatorname {seq}^{1-1}}(A)$
.
Fact 2.15.
![]() ${\operatorname {Part}}(A)\preccurlyeq \mathscr {P}(A^2)$
.
${\operatorname {Part}}(A)\preccurlyeq \mathscr {P}(A^2)$
.
Proof The function that maps each partition P of A to
![]() $\sim _P$
is an injection from
$\sim _P$
is an injection from
![]() ${\operatorname {Part}}(A)$
into
${\operatorname {Part}}(A)$
into
![]() $\mathscr {P}(A^2)$
.
$\mathscr {P}(A^2)$
.
Corollary 2.16. If A is power Dedekind finite, then
![]() ${\operatorname {Part}}(A)$
, and hence also
${\operatorname {Part}}(A)$
, and hence also
![]() ${\operatorname {Part}_{\operatorname {fin}}}(A)$
and
${\operatorname {Part}_{\operatorname {fin}}}(A)$
and
![]() $\mathscr {B}(A)$
, are Dedekind finite.
$\mathscr {B}(A)$
, are Dedekind finite.
Proof If A is power Dedekind finite, so is
![]() $A^2$
by Fact 2.6, and thus
$A^2$
by Fact 2.6, and thus
![]() $\mathscr {P}(A^2)$
is Dedekind finite, which implies that also
$\mathscr {P}(A^2)$
is Dedekind finite, which implies that also
![]() ${\operatorname {Part}}(A)$
,
${\operatorname {Part}}(A)$
,
![]() ${\operatorname {Part}_{\operatorname {fin}}}(A)$
and
${\operatorname {Part}_{\operatorname {fin}}}(A)$
and
![]() $\mathscr {B}(A)$
are Dedekind finite by Fact 2.15.
$\mathscr {B}(A)$
are Dedekind finite by Fact 2.15.
Fact 2.17.
![]() ${\mathscr {B}_{\operatorname {fin}}}(A)\preccurlyeq \operatorname {fin}(\operatorname {fin}(A))$
.
${\mathscr {B}_{\operatorname {fin}}}(A)\preccurlyeq \operatorname {fin}(\operatorname {fin}(A))$
.
Proof The function that maps each
![]() $P\in {\mathscr {B}_{\operatorname {fin}}}(A)$
to
$P\in {\mathscr {B}_{\operatorname {fin}}}(A)$
to
![]() ${\operatorname {ns}}(P)$
is an injection from
${\operatorname {ns}}(P)$
is an injection from
![]() ${\mathscr {B}_{\operatorname {fin}}}(A)$
into
${\mathscr {B}_{\operatorname {fin}}}(A)$
into
![]() $\operatorname {fin}(\operatorname {fin}(A))$
.
$\operatorname {fin}(\operatorname {fin}(A))$
.
Fact 2.18.
![]() ${\mathscr {B}_{\operatorname {fin}}}(A)\preccurlyeq {\operatorname {Part}_{\operatorname {fin}}}(A)$
.
${\mathscr {B}_{\operatorname {fin}}}(A)\preccurlyeq {\operatorname {Part}_{\operatorname {fin}}}(A)$
.
Proof If A is finite, then
![]() ${\mathscr {B}_{\operatorname {fin}}}(A)={\operatorname {Part}_{\operatorname {fin}}}(A)$
; otherwise, the function that maps each
${\mathscr {B}_{\operatorname {fin}}}(A)={\operatorname {Part}_{\operatorname {fin}}}(A)$
; otherwise, the function that maps each
![]() $P\in {\mathscr {B}_{\operatorname {fin}}}(A)$
to
$P\in {\mathscr {B}_{\operatorname {fin}}}(A)$
to
![]() ${\operatorname {ns}}(P)\cup \{\bigcup (P\setminus {\operatorname {ns}}(P))\}$
is an injection from
${\operatorname {ns}}(P)\cup \{\bigcup (P\setminus {\operatorname {ns}}(P))\}$
is an injection from
![]() ${\mathscr {B}_{\operatorname {fin}}}(A)$
into
${\mathscr {B}_{\operatorname {fin}}}(A)$
into
![]() ${\operatorname {Part}_{\operatorname {fin}}}(A)$
.
${\operatorname {Part}_{\operatorname {fin}}}(A)$
.
Fact 2.19. If
![]() $|A|\geqslant 5$
, then
$|A|\geqslant 5$
, then
![]() $\operatorname {fin}(A)\preccurlyeq {\mathscr {B}_{\operatorname {fin}}}(A)$
and
$\operatorname {fin}(A)\preccurlyeq {\mathscr {B}_{\operatorname {fin}}}(A)$
and
![]() $\mathscr {P}(A)\preccurlyeq {\operatorname {Part}_{\operatorname {fin}}}(A)$
.
$\mathscr {P}(A)\preccurlyeq {\operatorname {Part}_{\operatorname {fin}}}(A)$
.
Proof Let
![]() $E=\{a,b,c,d,e\}$
be a
$E=\{a,b,c,d,e\}$
be a
![]() $5$
-element subset of A. We define functions
$5$
-element subset of A. We define functions
![]() $f:\operatorname {fin}(A)\to {\mathscr {B}_{\operatorname {fin}}}(A)$
and
$f:\operatorname {fin}(A)\to {\mathscr {B}_{\operatorname {fin}}}(A)$
and
![]() $g:\mathscr {P}(A)\to {\operatorname {Part}_{\operatorname {fin}}}(A)$
by setting, for
$g:\mathscr {P}(A)\to {\operatorname {Part}_{\operatorname {fin}}}(A)$
by setting, for
![]() $B\in \operatorname {fin}(A)$
and
$B\in \operatorname {fin}(A)$
and
![]() $C\in \mathscr {P}(A)$
,
$C\in \mathscr {P}(A)$
,
 $$\begin{align*}f(B)= \begin{cases} (\{B\}\cup[A\setminus B]^1)\setminus\{\varnothing\}, & \text{if}\ B \text{is not a singleton,}\\ \{\{a,x\},E\setminus\{a,x\}\}\cup[A\setminus(B\cup E)]^1, & \text{if}\ B=\{x\}\ \text{for some}\ x\neq a,\\ \{\{a\},\{b,c\},\{d,e\}\}\cup[A\setminus E]^1, & \text{if}\ B=\{a\}, \end{cases} \end{align*}$$
$$\begin{align*}f(B)= \begin{cases} (\{B\}\cup[A\setminus B]^1)\setminus\{\varnothing\}, & \text{if}\ B \text{is not a singleton,}\\ \{\{a,x\},E\setminus\{a,x\}\}\cup[A\setminus(B\cup E)]^1, & \text{if}\ B=\{x\}\ \text{for some}\ x\neq a,\\ \{\{a\},\{b,c\},\{d,e\}\}\cup[A\setminus E]^1, & \text{if}\ B=\{a\}, \end{cases} \end{align*}$$
and
 $$\begin{align*}g(C)= \begin{cases} \{C,A\setminus C\}\setminus\{\varnothing\}, & \text{if}\ a\notin C,\\ (\{C,A\setminus(C\cup E)\}\cup[E\setminus C]^1)\setminus\{\varnothing\}, & \text{if}\ a\in C, |C\cap E|\leqslant3,\\ \{C\setminus\{a\},\{a\},E\setminus C,A\setminus(C\cup E)\}\setminus\{\varnothing\}, & \text{if}\ a\in C, |C\cap E|=4,\\ \{C\setminus\{b,c,d,e\},\{b,c\},\{d,e\},A\setminus C\}\setminus\{\varnothing\}, & \text{if}\ E\subseteq C, \end{cases} \end{align*}$$
$$\begin{align*}g(C)= \begin{cases} \{C,A\setminus C\}\setminus\{\varnothing\}, & \text{if}\ a\notin C,\\ (\{C,A\setminus(C\cup E)\}\cup[E\setminus C]^1)\setminus\{\varnothing\}, & \text{if}\ a\in C, |C\cap E|\leqslant3,\\ \{C\setminus\{a\},\{a\},E\setminus C,A\setminus(C\cup E)\}\setminus\{\varnothing\}, & \text{if}\ a\in C, |C\cap E|=4,\\ \{C\setminus\{b,c,d,e\},\{b,c\},\{d,e\},A\setminus C\}\setminus\{\varnothing\}, & \text{if}\ E\subseteq C, \end{cases} \end{align*}$$
where
![]() $[D]^1$
denotes the set of
$[D]^1$
denotes the set of
![]() $1$
-element subsets of D. It is easy to see that f and g are injective.
$1$
-element subsets of D. It is easy to see that f and g are injective.
The following corollary immediately follows from Facts 2.9 and 2.19.
Corollary 2.20. If A is infinite, then
![]() ${\mathscr {B}_{\operatorname {fin}}}(A)$
and
${\mathscr {B}_{\operatorname {fin}}}(A)$
and
![]() $\mathscr {B}(A)$
are power Dedekind infinite.
$\mathscr {B}(A)$
are power Dedekind infinite.
For infinite sets A, the relations between the cardinalities of
![]() $\operatorname {fin}(A)$
,
$\operatorname {fin}(A)$
,
![]() $\mathscr {P}(A)$
,
$\mathscr {P}(A)$
,
![]() ${\mathscr {B}_{\operatorname {fin}}}(A)$
,
${\mathscr {B}_{\operatorname {fin}}}(A)$
,
![]() $\mathscr {B}(A)$
,
$\mathscr {B}(A)$
,
![]() ${\operatorname {Part}_{\operatorname {fin}}}(A)$
,
${\operatorname {Part}_{\operatorname {fin}}}(A)$
,
![]() ${\operatorname {Part}}(A)$
, and
${\operatorname {Part}}(A)$
, and
![]() $\mathscr {P}(A^2)$
can be visualized by Figure 1 (where for two sets X and Y,
$\mathscr {P}(A^2)$
can be visualized by Figure 1 (where for two sets X and Y,
![]() $X\longrightarrow Y$
means
$X\longrightarrow Y$
means
![]() $|X|\leqslant |Y|$
,
$|X|\leqslant |Y|$
, ![]() means
means
![]() $|X|<|Y|$
, and
$|X|<|Y|$
, and ![]() means
means
![]() $|X|\neq |Y|$
).
$|X|\neq |Y|$
).

Figure 1 Relations between the cardinalities of some sets.
In Figure 1, the
![]() $\leqslant $
-relations have already been established, and the inequalities
$\leqslant $
-relations have already been established, and the inequalities
![]() $|\mathrm {fin}(A)|<|\mathscr {P}(A)|$
and
$|\mathrm {fin}(A)|<|\mathscr {P}(A)|$
and
![]() $|\mathrm {fin}(A)|<|\mathscr {B}(A)|$
are proved in [Reference Halbeisen and Shelah5, Theorem 3] and [Reference Phansamdaeng and Vejjajiva10, Theorem 3.7], respectively. The inequalities
$|\mathrm {fin}(A)|<|\mathscr {B}(A)|$
are proved in [Reference Halbeisen and Shelah5, Theorem 3] and [Reference Phansamdaeng and Vejjajiva10, Theorem 3.7], respectively. The inequalities
![]() $|\mathscr {B}_{\mathrm {fin}}(A)|<|\mathrm {Part}_{\mathrm {fin}}(A)|$
and
$|\mathscr {B}_{\mathrm {fin}}(A)|<|\mathrm {Part}_{\mathrm {fin}}(A)|$
and
![]() $|\mathscr {B}_{\mathrm {fin}}(A)|\neq |\mathscr {P}(A)|$
will be proved in Section 4. The other relations not indicted in the figure cannot be proved in
$|\mathscr {B}_{\mathrm {fin}}(A)|\neq |\mathscr {P}(A)|$
will be proved in Section 4. The other relations not indicted in the figure cannot be proved in
![]() $\mathsf {ZF}$
, as shown in the next section.
$\mathsf {ZF}$
, as shown in the next section.
3 Permutation models and consistency results
We refer the readers to [Reference Halbeisen4, Chapter 8] or [Reference Jech6, Chapter 4] for an introduction to the theory of permutation models. Permutation models are not models of
![]() $\mathsf {ZF}$
; they are models of
$\mathsf {ZF}$
; they are models of
![]() $\mathsf {ZFA}$
(the Zermelo–Fraenkel set theory with atoms). Nevertheless, they indirectly give, via the Jech–Sochor theorem (cf. [Reference Halbeisen4, Theorem 17.2] or [Reference Jech6, Theorem 6.1]), models of
$\mathsf {ZFA}$
(the Zermelo–Fraenkel set theory with atoms). Nevertheless, they indirectly give, via the Jech–Sochor theorem (cf. [Reference Halbeisen4, Theorem 17.2] or [Reference Jech6, Theorem 6.1]), models of
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
Let A be the set of atoms, let
![]() $\mathcal {G}$
be a group of permutations of A, and let
$\mathcal {G}$
be a group of permutations of A, and let
![]() $\mathfrak {F}$
be a normal filter on
$\mathfrak {F}$
be a normal filter on
![]() $\mathcal {G}$
. We write
$\mathcal {G}$
. We write
![]() ${\operatorname {sym}_{\mathcal {G}}}(x)$
for the set
${\operatorname {sym}_{\mathcal {G}}}(x)$
for the set
![]() $\{\pi \in \mathcal {G}\mid \pi x=x\}$
, where
$\{\pi \in \mathcal {G}\mid \pi x=x\}$
, where
![]() $\pi \in \mathcal {G}$
extends to a permutation of the universe by
$\pi \in \mathcal {G}$
extends to a permutation of the universe by
Then x belongs to the permutation model
![]() $\mathcal {V}$
determined by
$\mathcal {V}$
determined by
![]() $\mathcal {G}$
and
$\mathcal {G}$
and
![]() $\mathfrak {F}$
if and only if
$\mathfrak {F}$
if and only if
![]() $x\subseteq \mathcal {V}$
and
$x\subseteq \mathcal {V}$
and
![]() ${\operatorname {sym}_{\mathcal {G}}}(x)\in \mathfrak {F}$
.
${\operatorname {sym}_{\mathcal {G}}}(x)\in \mathfrak {F}$
.
For each
![]() $E\subseteq A$
, we write
$E\subseteq A$
, we write
![]() ${\operatorname {fix}_{\mathcal {G}}}(E)$
for the set
${\operatorname {fix}_{\mathcal {G}}}(E)$
for the set
![]() $\{\pi \in \mathcal {G}\mid \forall a\in E(\pi a=a)\}$
. Let
$\{\pi \in \mathcal {G}\mid \forall a\in E(\pi a=a)\}$
. Let
![]() $\mathcal {I}\subseteq \mathscr {P}(A)$
be a normal ideal and let
$\mathcal {I}\subseteq \mathscr {P}(A)$
be a normal ideal and let
![]() $\mathfrak {F}$
be the normal filter on
$\mathfrak {F}$
be the normal filter on
![]() $\mathcal {G}$
generated by the subgroups
$\mathcal {G}$
generated by the subgroups
![]() $\{{\operatorname {fix}_{\mathcal {G}}}(E)\mid E\in \mathcal {I}\}$
. Then x belongs to the permutation model
$\{{\operatorname {fix}_{\mathcal {G}}}(E)\mid E\in \mathcal {I}\}$
. Then x belongs to the permutation model
![]() $\mathcal {V}$
determined by
$\mathcal {V}$
determined by
![]() $\mathcal {G}$
and
$\mathcal {G}$
and
![]() $\mathcal {I}$
if and only if
$\mathcal {I}$
if and only if
![]() $x\subseteq \mathcal {V}$
and there exists an
$x\subseteq \mathcal {V}$
and there exists an
![]() $E\in \mathcal {I}$
such that
$E\in \mathcal {I}$
such that
![]() ${\operatorname {fix}_{\mathcal {G}}}(E)\subseteq {\operatorname {sym}_{\mathcal {G}}}(x)$
; that is, every
${\operatorname {fix}_{\mathcal {G}}}(E)\subseteq {\operatorname {sym}_{\mathcal {G}}}(x)$
; that is, every
![]() $\pi \in \mathcal {G}$
fixing E pointwise also fixes x. Such an E is called a support of x.
$\pi \in \mathcal {G}$
fixing E pointwise also fixes x. Such an E is called a support of x.
3.1 A model for
 $|\mathscr {B}(A)|\leqslant ^\ast |A|$
and
$|\mathscr {B}(A)|\leqslant ^\ast |A|$
and
 $|\mathscr {B}(A)|<|\mathscr {P}(A)|$
$|\mathscr {B}(A)|<|\mathscr {P}(A)|$
We construct a permutation model
![]() $\mathcal {V}_{\mathscr {B}}$
in which the set A of atoms satisfies
$\mathcal {V}_{\mathscr {B}}$
in which the set A of atoms satisfies
![]() $|\mathscr {B}(A)|\leqslant ^\ast |A|$
and
$|\mathscr {B}(A)|\leqslant ^\ast |A|$
and
![]() $|\mathscr {B}(A)|<|\mathscr {P}(A)|$
. The atoms are constructed by recursion as follows:
$|\mathscr {B}(A)|<|\mathscr {P}(A)|$
. The atoms are constructed by recursion as follows:
-
(i)
 $A_0=\varnothing $
and
$A_0=\varnothing $
and
 $\mathcal {G}_0=\{\varnothing \}$
is the group of all permutations of
$\mathcal {G}_0=\{\varnothing \}$
is the group of all permutations of
 $A_0$
.
$A_0$
. -
(ii)
 $A_{n+1}=A_n\cup \{(n,P,k)\mid P\in \mathscr {B}(A_n)\text { and }k\in \omega \}$
.
$A_{n+1}=A_n\cup \{(n,P,k)\mid P\in \mathscr {B}(A_n)\text { and }k\in \omega \}$
. -
(iii)
 $\mathcal {G}_{n+1}$
is the group of permutations of
$\mathcal {G}_{n+1}$
is the group of permutations of
 $A_{n+1}$
consisting of all permutations h for which there exists a
$A_{n+1}$
consisting of all permutations h for which there exists a
 $g\in \mathcal {G}_n$
such that:
$g\in \mathcal {G}_n$
such that:-
•
 $g=h{\upharpoonright } A_n$
;
$g=h{\upharpoonright } A_n$
; -
• for each
 $P\in \mathscr {B}(A_n)$
, there exists a permutation q of
$P\in \mathscr {B}(A_n)$
, there exists a permutation q of
 $\omega $
such that
$\omega $
such that
 $h(n,P,k)=(n,\{g[D]\mid D\in P\},q(k))$
for all
$h(n,P,k)=(n,\{g[D]\mid D\in P\},q(k))$
for all
 $k\in \omega $
.
$k\in \omega $
.
-
Let
![]() $A=\bigcup _{n\in \omega }A_n$
be the set of atoms, let
$A=\bigcup _{n\in \omega }A_n$
be the set of atoms, let
![]() $\mathcal {G}$
be the group of permutations of A consisting of all permutations
$\mathcal {G}$
be the group of permutations of A consisting of all permutations
![]() $\pi $
such that
$\pi $
such that
![]() $\pi {\upharpoonright } A_n\in \mathcal {G}_n$
for all
$\pi {\upharpoonright } A_n\in \mathcal {G}_n$
for all
![]() $n\in \omega $
, and let
$n\in \omega $
, and let
![]() $\mathfrak {F}$
be the normal filter on
$\mathfrak {F}$
be the normal filter on
![]() $\mathcal {G}$
generated by the subgroups
$\mathcal {G}$
generated by the subgroups
![]() $\{{\operatorname {fix}_{\mathcal {G}}}(A_n)\mid n\in \omega \}$
. The permutation model determined by
$\{{\operatorname {fix}_{\mathcal {G}}}(A_n)\mid n\in \omega \}$
. The permutation model determined by
![]() $\mathcal {G}$
and
$\mathcal {G}$
and
![]() $\mathfrak {F}$
is denoted by
$\mathfrak {F}$
is denoted by
![]() $\mathcal {V}_{\mathscr {B}}$
.
$\mathcal {V}_{\mathscr {B}}$
.
Lemma 3.1. For every
![]() $P\in \mathscr {B}(A)$
,
$P\in \mathscr {B}(A)$
,
![]() $P\in \mathcal {V}_{\mathscr {B}}$
if and only if
$P\in \mathcal {V}_{\mathscr {B}}$
if and only if
![]() ${\operatorname {ns}}(P)\subseteq \mathscr {P}(A_m)$
for some
${\operatorname {ns}}(P)\subseteq \mathscr {P}(A_m)$
for some
![]() $m\in \omega $
.
$m\in \omega $
.
Proof Let
![]() $P\in \mathscr {B}(A)$
. If
$P\in \mathscr {B}(A)$
. If
![]() ${\operatorname {ns}}(P)\subseteq \mathscr {P}(A_m)$
for some
${\operatorname {ns}}(P)\subseteq \mathscr {P}(A_m)$
for some
![]() $m\in \omega $
, then clearly
$m\in \omega $
, then clearly
![]() ${\operatorname {fix}_{\mathcal {G}}}(A_m)\subseteq {\operatorname {sym}_{\mathcal {G}}}(P)$
, which implies that
${\operatorname {fix}_{\mathcal {G}}}(A_m)\subseteq {\operatorname {sym}_{\mathcal {G}}}(P)$
, which implies that
![]() $P\in \mathcal {V}_{\mathscr {B}}$
. For the other direction, suppose
$P\in \mathcal {V}_{\mathscr {B}}$
. For the other direction, suppose
![]() $P\in \mathcal {V}_{\mathscr {B}}$
and let
$P\in \mathcal {V}_{\mathscr {B}}$
and let
![]() $m\in \omega $
be such that
$m\in \omega $
be such that
![]() ${\operatorname {fix}_{\mathcal {G}}}(A_m)\subseteq {\operatorname {sym}_{\mathcal {G}}}(P)$
; that is, every
${\operatorname {fix}_{\mathcal {G}}}(A_m)\subseteq {\operatorname {sym}_{\mathcal {G}}}(P)$
; that is, every
![]() $\pi \in \mathcal {G}$
fixing
$\pi \in \mathcal {G}$
fixing
![]() $A_m$
pointwise also fixes P. We claim
$A_m$
pointwise also fixes P. We claim
![]() ${\operatorname {ns}}(P)\subseteq \mathscr {P}(A_m)$
. Assume towards a contradiction that
${\operatorname {ns}}(P)\subseteq \mathscr {P}(A_m)$
. Assume towards a contradiction that
![]() $x\sim _Py$
for some distinct
$x\sim _Py$
for some distinct
![]() $x,y$
such that one of x and y is not in
$x,y$
such that one of x and y is not in
![]() $A_m$
. Suppose that
$A_m$
. Suppose that
![]() $x=(n,Q,k)$
and
$x=(n,Q,k)$
and
![]() $y=(n',Q',k')$
, and assume without loss of generality
$y=(n',Q',k')$
, and assume without loss of generality
![]() $n'\leqslant n$
. Then
$n'\leqslant n$
. Then
![]() $x\notin A_m$
and thus
$x\notin A_m$
and thus
![]() $m\leqslant n$
. Let
$m\leqslant n$
. Let
![]() $l\in \omega $
be such that
$l\in \omega $
be such that
![]() $(n,Q,l)\notin [y]_P$
and let q be the transposition that swaps k and l. Since P is finitary, such an l exists. Let h be the permutation of
$(n,Q,l)\notin [y]_P$
and let q be the transposition that swaps k and l. Since P is finitary, such an l exists. Let h be the permutation of
![]() $A_{n+1}$
such that h fixes
$A_{n+1}$
such that h fixes
![]() $A_n$
pointwise and for all
$A_n$
pointwise and for all
![]() $R\in \mathscr {B}(A_n)$
and all
$R\in \mathscr {B}(A_n)$
and all
![]() $j\in \omega $
,
$j\in \omega $
,
![]() $h(n,R,j)=(n,R,q(j))$
if
$h(n,R,j)=(n,R,q(j))$
if
![]() $R=Q$
, and
$R=Q$
, and
![]() $h(n,R,j)=(n,R,j)$
otherwise. Then
$h(n,R,j)=(n,R,j)$
otherwise. Then
![]() $h\in \mathcal {G}_{n+1}$
fixes
$h\in \mathcal {G}_{n+1}$
fixes
![]() $A_{n+1}\setminus \{x,(n,Q,l)\}$
pointwise. Hence
$A_{n+1}\setminus \{x,(n,Q,l)\}$
pointwise. Hence
![]() $h(y)=y$
. Extend h in a straightforward way to some
$h(y)=y$
. Extend h in a straightforward way to some
![]() $\pi \in \mathcal {G}$
. Then
$\pi \in \mathcal {G}$
. Then
![]() $\pi \in {\operatorname {fix}_{\mathcal {G}}}(A_m\cup \{y\})$
and
$\pi \in {\operatorname {fix}_{\mathcal {G}}}(A_m\cup \{y\})$
and
![]() $\pi (x)=(n,Q,l)\notin [y]_P$
. Thus
$\pi (x)=(n,Q,l)\notin [y]_P$
. Thus
![]() $\pi $
moves P, which is a contradiction.
$\pi $
moves P, which is a contradiction.
Lemma 3.2. In
![]() $\mathcal {V}_{\mathscr {B}}$
,
$\mathcal {V}_{\mathscr {B}}$
,
![]() $|\mathscr {B}(A)|\leqslant ^\ast |A|$
and
$|\mathscr {B}(A)|\leqslant ^\ast |A|$
and
![]() $|\mathscr {B}(A)|<|\mathscr {P}(A)|$
.
$|\mathscr {B}(A)|<|\mathscr {P}(A)|$
.
Proof Let
![]() $\Phi $
be the function on
$\Phi $
be the function on
![]() $\{P\in \mathscr {B}(A)\mid \exists m\in \omega ({\operatorname {ns}}(P)\subseteq \mathscr {P}(A_m))\}$
defined by
$\{P\in \mathscr {B}(A)\mid \exists m\in \omega ({\operatorname {ns}}(P)\subseteq \mathscr {P}(A_m))\}$
defined by
where
![]() $n_P$
is the least
$n_P$
is the least
![]() $m\in \omega $
such that
$m\in \omega $
such that
![]() ${\operatorname {ns}}(P)\subseteq \mathscr {P}(A_m)$
. Clearly,
${\operatorname {ns}}(P)\subseteq \mathscr {P}(A_m)$
. Clearly,
![]() $\Phi \in \mathcal {V}_{\mathscr {B}}$
. In
$\Phi \in \mathcal {V}_{\mathscr {B}}$
. In
![]() $\mathcal {V}_{\mathscr {B}}$
, by Lemma 3.1,
$\mathcal {V}_{\mathscr {B}}$
, by Lemma 3.1,
![]() $\Phi $
is an injection from
$\Phi $
is an injection from
![]() $\mathscr {B}(A)$
into
$\mathscr {B}(A)$
into
![]() $\mathscr {P}(A)$
, and the sets in the range of
$\mathscr {P}(A)$
, and the sets in the range of
![]() $\Phi $
are pairwise disjoint, which implies that
$\Phi $
are pairwise disjoint, which implies that
![]() $|\mathscr {B}(A)|\leqslant ^\ast |A|$
. Since
$|\mathscr {B}(A)|\leqslant ^\ast |A|$
. Since
![]() $|\mathscr {P}(A)|\nleqslant ^\ast |A|$
by Cantor’s theorem, it follows that
$|\mathscr {P}(A)|\nleqslant ^\ast |A|$
by Cantor’s theorem, it follows that
![]() $|\mathscr {B}(A)|<|\mathscr {P}(A)|$
.
$|\mathscr {B}(A)|<|\mathscr {P}(A)|$
.
Now the next theorem immediately follows from Lemma 3.2 and the Jech–Sochor theorem.
Theorem 3.3. It is consistent with
![]() $\mathsf {ZF}$
that there exists an infinite set A for which
$\mathsf {ZF}$
that there exists an infinite set A for which
![]() $|\mathscr {B}(A)|\leqslant ^\ast |A|$
and
$|\mathscr {B}(A)|\leqslant ^\ast |A|$
and
![]() $|\mathscr {B}(A)|<|\mathscr {P}(A)|$
.
$|\mathscr {B}(A)|<|\mathscr {P}(A)|$
.
3.2 A model for
 $|\mathscr {P}(A)|<|\mathscr {B}(A)|<|\mathrm {Part}_{\mathrm {fin}}(A)|$
$|\mathscr {P}(A)|<|\mathscr {B}(A)|<|\mathrm {Part}_{\mathrm {fin}}(A)|$
We show that the ordered Mostowski model
![]() $\mathcal {V}_{\mathrm {M}}$
(cf. [Reference Halbeisen4, pp. 198–202] or [Reference Jech6, Section 4.5]) is a model of this kind. Recall that the set A of atoms carries an ordering
$\mathcal {V}_{\mathrm {M}}$
(cf. [Reference Halbeisen4, pp. 198–202] or [Reference Jech6, Section 4.5]) is a model of this kind. Recall that the set A of atoms carries an ordering
![]() $<_{\mathrm {M}}$
which is isomorphic to the ordering of the rational numbers, the permutation group
$<_{\mathrm {M}}$
which is isomorphic to the ordering of the rational numbers, the permutation group
![]() $\mathcal {G}$
consists of all automorphisms of
$\mathcal {G}$
consists of all automorphisms of
![]() $\langle A,<_{\mathrm {M}}\rangle$
, and
$\langle A,<_{\mathrm {M}}\rangle$
, and
![]() $\mathcal {V}_{\mathrm {M}}$
is determined by
$\mathcal {V}_{\mathrm {M}}$
is determined by
![]() $\mathcal {G}$
and finite supports. Clearly, the ordering
$\mathcal {G}$
and finite supports. Clearly, the ordering
![]() $<_{\mathrm {M}}$
belongs to
$<_{\mathrm {M}}$
belongs to
![]() $\mathcal {V}_{\mathrm {M}}$
(cf. [Reference Halbeisen4, Lemma 8.10]). In
$\mathcal {V}_{\mathrm {M}}$
(cf. [Reference Halbeisen4, Lemma 8.10]). In
![]() $\mathcal {V}_{\mathrm {M}}$
, A is infinite but power Dedekind finite (cf. [Reference Halbeisen4, Lemma 8.13]), and thus, by Fact 2.6 and Corollary 2.16,
$\mathcal {V}_{\mathrm {M}}$
, A is infinite but power Dedekind finite (cf. [Reference Halbeisen4, Lemma 8.13]), and thus, by Fact 2.6 and Corollary 2.16,
![]() $\mathscr {P}(A^2)$
and
$\mathscr {P}(A^2)$
and
![]() $\mathscr {B}(A)$
are Dedekind finite.
$\mathscr {B}(A)$
are Dedekind finite.
Lemma 3.4. In
![]() $\mathcal {V}_{\mathrm {M}}$
,
$\mathcal {V}_{\mathrm {M}}$
,
![]() $\mathscr {B}(A)={\mathscr {B}_{\operatorname {fin}}}(A)$
.
$\mathscr {B}(A)={\mathscr {B}_{\operatorname {fin}}}(A)$
.
Proof Let
![]() $P\in \mathcal {V}_{\mathrm {M}}$
be a finitary partition of A and let E be a finite support of P. We claim
$P\in \mathcal {V}_{\mathrm {M}}$
be a finitary partition of A and let E be a finite support of P. We claim
![]() ${\operatorname {ns}}(P)\subseteq \mathscr {P}(E)$
. Assume towards a contradiction that
${\operatorname {ns}}(P)\subseteq \mathscr {P}(E)$
. Assume towards a contradiction that
![]() $x\sim _Py$
for some distinct
$x\sim _Py$
for some distinct
![]() $x,y$
such that
$x,y$
such that
![]() $x\notin E$
. Since P is finitary, we can find a
$x\notin E$
. Since P is finitary, we can find a
![]() $\pi \in {\operatorname {fix}_{\mathcal {G}}}(E\cup \{y\})$
such that
$\pi \in {\operatorname {fix}_{\mathcal {G}}}(E\cup \{y\})$
such that
![]() $\pi (x)\notin [y]_P$
. Hence
$\pi (x)\notin [y]_P$
. Hence
![]() $\pi $
moves P, contradicting that E is a support of P. Thus
$\pi $
moves P, contradicting that E is a support of P. Thus
![]() ${\operatorname {ns}}(P)\subseteq \mathscr {P}(E)$
, so
${\operatorname {ns}}(P)\subseteq \mathscr {P}(E)$
, so
![]() $P\in {\mathscr {B}_{\operatorname {fin}}}(A)$
.
$P\in {\mathscr {B}_{\operatorname {fin}}}(A)$
.
The next two lemmas are Lemmas 8.11(b) and 8.12 of [Reference Halbeisen4], respectively.
Lemma 3.5. Every
![]() $x\in \mathcal {V}_{\mathrm {M}}$
has a least support.
$x\in \mathcal {V}_{\mathrm {M}}$
has a least support.
Lemma 3.6. If E is an n-element subset of A, then E supports exactly
![]() $2^{2n+1}$
subsets of A.
$2^{2n+1}$
subsets of A.
Lemma 3.7. For each
![]() $n\in \omega $
, let
$n\in \omega $
, let
![]() $B_n^\star $
be the number of partitions of n without singleton blocks; that is,
$B_n^\star $
be the number of partitions of n without singleton blocks; that is,
If
![]() $n\geqslant 23$
, then
$n\geqslant 23$
, then
![]() $2^{2n+2}<B_n^\star $
.
$2^{2n+2}<B_n^\star $
.
Proof For each
![]() $n\in \omega $
, let
$n\in \omega $
, let
![]() $B_n$
be the nth Bell number; that is,
$B_n$
be the nth Bell number; that is,
![]() $B_n=|\mathscr {B}(n)|$
. Recall Dobinski’s formula (see, for example, [Reference Rota11]):
$B_n=|\mathscr {B}(n)|$
. Recall Dobinski’s formula (see, for example, [Reference Rota11]):
 $$\begin{align*}B_n=\frac{1}{e}\sum_{k=0}^\infty\frac{k^n}{k!}. \end{align*}$$
$$\begin{align*}B_n=\frac{1}{e}\sum_{k=0}^\infty\frac{k^n}{k!}. \end{align*}$$
It is easy to see that
![]() $B_n=B_n^\star +B_{n+1}^\star $
. Hence, for
$B_n=B_n^\star +B_{n+1}^\star $
. Hence, for
![]() $n\geqslant 23$
, we have
$n\geqslant 23$
, we have
Lemma 3.8 In
![]() $\mathcal {V}_{\mathrm {M}}$
,
$\mathcal {V}_{\mathrm {M}}$
,
![]() $|\mathscr {P}(A)|<|\mathscr {B}(A)|<|\mathrm {Part}_{\mathrm {fin}}(A)|<|\mathrm {Part}(A)|<|\mathscr {P}(A^2)|$
.
$|\mathscr {P}(A)|<|\mathscr {B}(A)|<|\mathrm {Part}_{\mathrm {fin}}(A)|<|\mathrm {Part}(A)|<|\mathscr {P}(A^2)|$
.
Proof In
![]() $\mathcal {V}_{\mathrm {M}}$
, since
$\mathcal {V}_{\mathrm {M}}$
, since
![]() $\mathscr {P}(A^2)$
is Dedekind finite, and the injections constructed in the proofs of Facts 2.15 and 2.18 are clearly not surjective, it follows that
$\mathscr {P}(A^2)$
is Dedekind finite, and the injections constructed in the proofs of Facts 2.15 and 2.18 are clearly not surjective, it follows that
![]() $|\mathscr {B}_{\mathrm {fin}}(A)|<|\mathrm {Part}_{\mathrm {fin}}(A)|<|\mathrm {Part}(A)|<|\mathscr {P}(A^2)|$
. By Lemma 3.4, it remains to show that
$|\mathscr {B}_{\mathrm {fin}}(A)|<|\mathrm {Part}_{\mathrm {fin}}(A)|<|\mathrm {Part}(A)|<|\mathscr {P}(A^2)|$
. By Lemma 3.4, it remains to show that
![]() $|\mathscr {P}(A)|<|\mathscr {B}(A)|$
.
$|\mathscr {P}(A)|<|\mathscr {B}(A)|$
.
For a finite subset E of A, we can use
![]() $<_{\mathrm {M}}$
to define an ordering of the subsets of A supported by E and an ordering of the finitary partitions P of A with
$<_{\mathrm {M}}$
to define an ordering of the subsets of A supported by E and an ordering of the finitary partitions P of A with
![]() ${\operatorname {ns}}(P)\subseteq \mathscr {P}(E)$
. Let
${\operatorname {ns}}(P)\subseteq \mathscr {P}(E)$
. Let
![]() $D=\{a_i\mid i<46\}$
be a
$D=\{a_i\mid i<46\}$
be a
![]() $46$
-element subset of A. In
$46$
-element subset of A. In
![]() $\mathcal {V}_{\mathrm {M}}$
, we define an injection f from
$\mathcal {V}_{\mathrm {M}}$
, we define an injection f from
![]() $\mathscr {P}(A)$
into
$\mathscr {P}(A)$
into
![]() $\mathscr {B}(A)$
as follows.
$\mathscr {B}(A)$
as follows.
Let
![]() $C\in \mathcal {V}_{\mathrm {M}}$
be a subset of A. By Lemma 3.5, C has a least support E. Suppose that C is the kth subset of A with E as its least support. Let
$C\in \mathcal {V}_{\mathrm {M}}$
be a subset of A. By Lemma 3.5, C has a least support E. Suppose that C is the kth subset of A with E as its least support. Let
![]() $n=|D\bigtriangleup E|$
, where
$n=|D\bigtriangleup E|$
, where
![]() $\bigtriangleup $
denotes the symmetric difference. Now, if
$\bigtriangleup $
denotes the symmetric difference. Now, if
![]() $|E|\geqslant 23$
, define
$|E|\geqslant 23$
, define
![]() $f(C)$
to be the kth finitary partition P of A with
$f(C)$
to be the kth finitary partition P of A with
![]() $\bigcup {\operatorname {ns}}(P)=E$
; otherwise, define
$\bigcup {\operatorname {ns}}(P)=E$
; otherwise, define
![]() $f(C)$
to be the
$f(C)$
to be the
![]() $(B_n^\star -k-1)$
th finitary partition P of A with
$(B_n^\star -k-1)$
th finitary partition P of A with
![]() $\bigcup {\operatorname {ns}}(P)=D\bigtriangleup E$
. In the second case,
$\bigcup {\operatorname {ns}}(P)=D\bigtriangleup E$
. In the second case,
![]() $n\geqslant 23$
, and thus
$n\geqslant 23$
, and thus
![]() $B_n^\star -k-1>2^{2n+1}$
by Lemmas 3.6 and 3.7. Thus f is injective. Since D is a finite support of f, it follows that
$B_n^\star -k-1>2^{2n+1}$
by Lemmas 3.6 and 3.7. Thus f is injective. Since D is a finite support of f, it follows that
![]() $f\in \mathcal {V}_{\mathrm {M}}$
.
$f\in \mathcal {V}_{\mathrm {M}}$
.
Finally, since
![]() $\mathscr {B}(A)$
is Dedekind finite and f is not surjective, it follows that
$\mathscr {B}(A)$
is Dedekind finite and f is not surjective, it follows that
![]() $|\mathscr {P}(A)|<|\mathscr {B}(A)|$
.
$|\mathscr {P}(A)|<|\mathscr {B}(A)|$
.
Now the next theorem immediately follows from Lemmas 3.4 and 3.8 and the Jech–Sochor theorem.
Theorem 3.9. It is consistent with
![]() $\mathsf {ZF}$
that there exists an infinite set A for which
$\mathsf {ZF}$
that there exists an infinite set A for which
![]() $\mathscr {B}(A)={\mathscr {B}_{\operatorname {fin}}}(A)$
and
$\mathscr {B}(A)={\mathscr {B}_{\operatorname {fin}}}(A)$
and
![]() $|\mathscr {P}(A)|<|\mathscr {B}(A)|<|\mathrm {Part}_{\mathrm {fin}}(A)|<|\mathrm {Part}(A)|<|\mathscr {P}(A^2)|$
.
$|\mathscr {P}(A)|<|\mathscr {B}(A)|<|\mathrm {Part}_{\mathrm {fin}}(A)|<|\mathrm {Part}(A)|<|\mathscr {P}(A^2)|$
.
3.3 A model in which
 $\mathscr {B}(A)$
is incomparable with
$\mathscr {B}(A)$
is incomparable with
 $\mathscr {P}(A)$
or
$\mathscr {P}(A)$
or
 ${\operatorname {Part}_{\operatorname {fin}}}(A)$
${\operatorname {Part}_{\operatorname {fin}}}(A)$
We use a variation of the basic Fraenkel model (cf. [Reference Halbeisen4, pp. 195–196] or [Reference Jech6, Section 4.3]). Let A be an uncountable set of atoms, let
![]() $\mathcal {G}$
be the group of all permutations of A, and let
$\mathcal {G}$
be the group of all permutations of A, and let
![]() $\mathcal {V}_{\mathrm {F}}$
be the permutation model determined by
$\mathcal {V}_{\mathrm {F}}$
be the permutation model determined by
![]() $\mathcal {G}$
and countable supports.
$\mathcal {G}$
and countable supports.
Lemma 3.10. In
![]() $\mathcal {V}_{\mathrm {F}}$
,
$\mathcal {V}_{\mathrm {F}}$
,
![]() $|\mathscr {B}(A)|\nleqslant |\mathrm {Part}_{\mathrm {fin}}(A)|$
,
$|\mathscr {B}(A)|\nleqslant |\mathrm {Part}_{\mathrm {fin}}(A)|$
,
![]() $|\mathscr {B}_{\mathrm {fin}}(A)|\nleqslant |\mathscr {P}(A)|$
, and
$|\mathscr {B}_{\mathrm {fin}}(A)|\nleqslant |\mathscr {P}(A)|$
, and
![]() $|\mathscr {P}(A)|\nleqslant |\mathscr {B}(A)|$
.
$|\mathscr {P}(A)|\nleqslant |\mathscr {B}(A)|$
.
Proof (1)
![]() $|\mathscr {B}(A)|\nleqslant |\mathrm {Part}_{\mathrm {fin}}(A)|$
. Assume towards a contradiction that in
$|\mathscr {B}(A)|\nleqslant |\mathrm {Part}_{\mathrm {fin}}(A)|$
. Assume towards a contradiction that in
![]() $\mathcal {V}_{\mathrm {F}}$
there is an injection f from
$\mathcal {V}_{\mathrm {F}}$
there is an injection f from
![]() $\mathscr {B}(A)$
into
$\mathscr {B}(A)$
into
![]() ${\operatorname {Part}_{\operatorname {fin}}}(A)$
. Let B be a countable support of f. Let
${\operatorname {Part}_{\operatorname {fin}}}(A)$
. Let B be a countable support of f. Let
![]() $\{a_n\mid n\in \omega \}\subseteq A\setminus B$
with
$\{a_n\mid n\in \omega \}\subseteq A\setminus B$
with
![]() $a_i\neq a_j$
whenever
$a_i\neq a_j$
whenever
![]() $i\neq j$
. Consider the finitary partition
$i\neq j$
. Consider the finitary partition
![]() $P=\{\{a_{2n},a_{2n+1}\}\mid n\in \omega \}\cup [A\setminus \{a_n\mid n\in \omega \}]^1\in \mathcal {V}_{\mathrm {F}}$
. Since
$P=\{\{a_{2n},a_{2n+1}\}\mid n\in \omega \}\cup [A\setminus \{a_n\mid n\in \omega \}]^1\in \mathcal {V}_{\mathrm {F}}$
. Since
![]() $f(P)$
is a finite partition, there must be
$f(P)$
is a finite partition, there must be
![]() $i,j\in \omega $
with
$i,j\in \omega $
with
![]() $i\neq j$
such that
$i\neq j$
such that
![]() $a_{2i}$
and
$a_{2i}$
and
![]() $a_{2j}$
are in the same block of
$a_{2j}$
are in the same block of
![]() $f(P)$
. The transposition that swaps
$f(P)$
. The transposition that swaps
![]() $a_{2i}$
and
$a_{2i}$
and
![]() $a_{2i+1}$
fixes P, and thus also fixes
$a_{2i+1}$
fixes P, and thus also fixes
![]() $f(P)$
, which implies that
$f(P)$
, which implies that
![]() $a_{2i+1}$
and
$a_{2i+1}$
and
![]() $a_{2j}$
are also in the same block of
$a_{2j}$
are also in the same block of
![]() $f(P)$
. Hence, the transposition that swaps
$f(P)$
. Hence, the transposition that swaps
![]() $a_{2i+1}$
and
$a_{2i+1}$
and
![]() $a_{2j}$
fixes
$a_{2j}$
fixes
![]() $f(P)$
, but it moves P, contradicting that f is injective.
$f(P)$
, but it moves P, contradicting that f is injective.
(2)
![]() $|\mathscr {B}_{\mathrm {fin}}(A)|\nleqslant |\mathscr {P}(A)|$
. Assume towards a contradiction that in
$|\mathscr {B}_{\mathrm {fin}}(A)|\nleqslant |\mathscr {P}(A)|$
. Assume towards a contradiction that in
![]() $\mathcal {V}_{\mathrm {F}}$
there is an injection g from
$\mathcal {V}_{\mathrm {F}}$
there is an injection g from
![]() ${\mathscr {B}_{\operatorname {fin}}}(A)$
into
${\mathscr {B}_{\operatorname {fin}}}(A)$
into
![]() $\mathscr {P}(A)$
. Let C be a countable support of g. Let
$\mathscr {P}(A)$
. Let C be a countable support of g. Let
![]() $a_0,a_1,a_2,a_3$
be four distinct elements of
$a_0,a_1,a_2,a_3$
be four distinct elements of
![]() $A\setminus C$
. Consider the finitary partition
$A\setminus C$
. Consider the finitary partition
![]() $P=\{\{a_0,a_1\},\{a_2,a_3\}\}\cup [A\setminus \{a_0,a_1,a_2,a_3\}]^1\in \mathcal {V}_{\mathrm {F}}$
. Clearly, for any
$P=\{\{a_0,a_1\},\{a_2,a_3\}\}\cup [A\setminus \{a_0,a_1,a_2,a_3\}]^1\in \mathcal {V}_{\mathrm {F}}$
. Clearly, for any
![]() $i,j<4$
with
$i,j<4$
with
![]() $i\neq j$
, there is a
$i\neq j$
, there is a
![]() $\pi \in {\operatorname {fix}_{\mathcal {G}}}(C)$
such that
$\pi \in {\operatorname {fix}_{\mathcal {G}}}(C)$
such that
![]() $\pi (P)=P$
and
$\pi (P)=P$
and
![]() $\pi (a_i)=a_j$
. Hence,
$\pi (a_i)=a_j$
. Hence,
![]() $\{a_0,a_1,a_2,a_3\}\subseteq g(P)$
or
$\{a_0,a_1,a_2,a_3\}\subseteq g(P)$
or
![]() $\{a_0,a_1,a_2,a_3\}\subseteq A\setminus g(P)$
. Thus, the transposition that swaps
$\{a_0,a_1,a_2,a_3\}\subseteq A\setminus g(P)$
. Thus, the transposition that swaps
![]() $a_0$
and
$a_0$
and
![]() $a_2$
fixes
$a_2$
fixes
![]() $g(P)$
, but it moves P, contradicting that g is injective.
$g(P)$
, but it moves P, contradicting that g is injective.
(3)
![]() $|\mathscr {P}(A)|\nleqslant |\mathscr {B}(A)|$
. Assume towards a contradiction that in
$|\mathscr {P}(A)|\nleqslant |\mathscr {B}(A)|$
. Assume towards a contradiction that in
![]() $\mathcal {V}_{\mathrm {F}}$
there is an injection h from
$\mathcal {V}_{\mathrm {F}}$
there is an injection h from
![]() $\mathscr {P}(A)$
into
$\mathscr {P}(A)$
into
![]() $\mathscr {B}(A)$
. Let D be a countable support of h. Let C be a denumerable subset of
$\mathscr {B}(A)$
. Let D be a countable support of h. Let C be a denumerable subset of
![]() $A\setminus D$
. Take
$A\setminus D$
. Take
![]() $x\in C$
and
$x\in C$
and
![]() $y\in A\setminus (C\cup D)$
. We claim that
$y\in A\setminus (C\cup D)$
. We claim that
![]() $\{x\}\in h(C)$
. Assume not; since
$\{x\}\in h(C)$
. Assume not; since
![]() $h(C)$
is finitary, we can find a
$h(C)$
is finitary, we can find a
![]() $z\in C$
such that
$z\in C$
such that
![]() $z\notin [x]_{h(C)}$
, and then the transposition that swaps x and z would fix C but move
$z\notin [x]_{h(C)}$
, and then the transposition that swaps x and z would fix C but move
![]() $h(C)$
, which is a contradiction. Similarly,
$h(C)$
, which is a contradiction. Similarly,
![]() $\{y\}\in h(C)$
. Hence, the transposition that swaps x and y fixes
$\{y\}\in h(C)$
. Hence, the transposition that swaps x and y fixes
![]() $h(C)$
, but it moves C, contradicting that h is injective.
$h(C)$
, but it moves C, contradicting that h is injective.
Now the next theorem immediately follows from Fact 2.19, Lemma 3.10, and the Jech–Sochor theorem.
Theorem 3.11. It is consistent with
![]() $\mathsf {ZF}$
that there exists an infinite set A such that:
$\mathsf {ZF}$
that there exists an infinite set A such that:
-
(i)
 $|\mathscr {B}(A)|$
and
$|\mathscr {B}(A)|$
and
 $|\mathrm {Part}_{\mathrm {fin}}(A)|$
are incomparable;
$|\mathrm {Part}_{\mathrm {fin}}(A)|$
are incomparable; -
(ii)
 $|\mathscr {B}(A)|$
and
$|\mathscr {B}(A)|$
and
 $|\mathscr {P}(A)|$
are incomparable;
$|\mathscr {P}(A)|$
are incomparable; -
(iii)
 $|\mathscr {B}_{\mathrm {fin}}(A)|$
and
$|\mathscr {B}_{\mathrm {fin}}(A)|$
and
 $|\mathscr {P}(A)|$
are incomparable.
$|\mathscr {P}(A)|$
are incomparable.
As easily seen, for infinite well-orderable A,
![]() $|A|=|\mathrm {fin}(A)|=|\mathscr {B}_{\mathrm {fin}}(A)|$
and
$|A|=|\mathrm {fin}(A)|=|\mathscr {B}_{\mathrm {fin}}(A)|$
and
![]() $|\mathscr {P}(A)|=|\mathscr {B}(A)|=|\mathrm {Part}_{\mathrm {fin}}(A)|=|\mathrm {Part}(A)|=|\mathscr {P}(A^2)|$
. Therefore, Theorems 3.3, 3.9, and 3.11 show that Figure 1 is optimal in the sense that the
$|\mathscr {P}(A)|=|\mathscr {B}(A)|=|\mathrm {Part}_{\mathrm {fin}}(A)|=|\mathrm {Part}(A)|=|\mathscr {P}(A^2)|$
. Therefore, Theorems 3.3, 3.9, and 3.11 show that Figure 1 is optimal in the sense that the
![]() $\leqslant $
,
$\leqslant $
,
![]() $<$
, or
$<$
, or
![]() $\neq $
relations between the cardinalities of these sets not indicted in the figure cannot be proved in
$\neq $
relations between the cardinalities of these sets not indicted in the figure cannot be proved in
![]() $\mathsf {ZF}$
. However, we do not know whether
$\mathsf {ZF}$
. However, we do not know whether
![]() $|\mathrm {Part}_{\mathrm {fin}}(A)|<|\mathscr {B}(A)|$
for some infinite set A is consistent with
$|\mathrm {Part}_{\mathrm {fin}}(A)|<|\mathscr {B}(A)|$
for some infinite set A is consistent with
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
4 Theorems in
 $\mathsf {ZF}$
$\mathsf {ZF}$
In this section, we prove in
![]() $\mathsf {ZF}$
some results concerning
$\mathsf {ZF}$
some results concerning
![]() $\mathscr {B}(A)$
, as well as the inequalities
$\mathscr {B}(A)$
, as well as the inequalities
![]() $|\mathscr {B}_{\mathrm {fin}}(A)|<|\mathrm {Part}_{\mathrm {fin}}(A)|$
and
$|\mathscr {B}_{\mathrm {fin}}(A)|<|\mathrm {Part}_{\mathrm {fin}}(A)|$
and
![]() $|\mathscr {B}_{\mathrm {fin}}(A)|\neq |\mathscr {P}(A)|$
indicted in Figure 1.
$|\mathscr {B}_{\mathrm {fin}}(A)|\neq |\mathscr {P}(A)|$
indicted in Figure 1.
Although Cantor’s theorem may fail for
![]() $\mathscr {B}(A)$
, it does hold under the existence of auxiliary functions.
$\mathscr {B}(A)$
, it does hold under the existence of auxiliary functions.
Definition 4.1. Let f be a function on A. An auxiliary function for f is a function g defined on
![]() ${\operatorname {ran}}(f)$
such that, for all
${\operatorname {ran}}(f)$
such that, for all
![]() $z\in {\operatorname {ran}}(f)$
,
$z\in {\operatorname {ran}}(f)$
,
![]() $g(z)$
is a finitary partition of
$g(z)$
is a finitary partition of
![]() $f^{-1}[\{z\}]$
with at least one non-singleton block.
$f^{-1}[\{z\}]$
with at least one non-singleton block.
Lemma 4.2. From a function
![]() $f:A\to \mathscr {B}(A)$
and an auxiliary function for f, one can explicitly define a finitary partition of A not in
$f:A\to \mathscr {B}(A)$
and an auxiliary function for f, one can explicitly define a finitary partition of A not in
![]() ${\operatorname {ran}}(f)$
.
${\operatorname {ran}}(f)$
.
Proof Use Cantor’s diagonal construction. Let f be a function from A to
![]() $\mathscr {B}(A)$
and let g be an auxiliary function for f. Let h be the function on
$\mathscr {B}(A)$
and let g be an auxiliary function for f. Let h be the function on
![]() ${\operatorname {ran}}(f)$
defined by
${\operatorname {ran}}(f)$
defined by
 $$\begin{align*}h(P)= \begin{cases} \{\{z\}\mid f(z)=P\}, & \text{if}\ x\sim_Py\ \text{for some distinct}\ x,y\in f^{-1}[\{P\}],\\ g(P), & \text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}h(P)= \begin{cases} \{\{z\}\mid f(z)=P\}, & \text{if}\ x\sim_Py\ \text{for some distinct}\ x,y\in f^{-1}[\{P\}],\\ g(P), & \text{otherwise.} \end{cases} \end{align*}$$
Then
![]() $\bigcup _{P\in {\operatorname {ran}}(f)}h(P)$
is a finitary partition of A not in
$\bigcup _{P\in {\operatorname {ran}}(f)}h(P)$
is a finitary partition of A not in
![]() ${\operatorname {ran}}(f)$
.
${\operatorname {ran}}(f)$
.
4.1 A general result
We prove a general result which states that, if
![]() $\mathscr {B}(A)$
is Dedekind infinite, then there are no Dedekind finite-to-one functions from
$\mathscr {B}(A)$
is Dedekind infinite, then there are no Dedekind finite-to-one functions from
![]() $\mathscr {B}(A)$
to
$\mathscr {B}(A)$
to
![]() $\operatorname {fin}(A)$
.
$\operatorname {fin}(A)$
.
Lemma 4.3. For any infinite ordinal
![]() $\alpha $
, one can explicitly define an injection
$\alpha $
, one can explicitly define an injection
![]() $f:\alpha \times \alpha \to \alpha $
.
$f:\alpha \times \alpha \to \alpha $
.
Proof See [Reference Specker18, 2.1].
Lemma 4.4. From an infinite ordinal
![]() $\alpha $
, one can explicitly define an injection
$\alpha $
, one can explicitly define an injection
![]() $f:\operatorname {fin}(\alpha )\to \alpha $
.
$f:\operatorname {fin}(\alpha )\to \alpha $
.
Proof See [Reference Halbeisen4, Theorem 5.19].
Lemma 4.5. From a finite-to-one function
![]() $f:\alpha \to A$
, where
$f:\alpha \to A$
, where
![]() $\alpha $
is an infinite ordinal, one can explicitly define an injection
$\alpha $
is an infinite ordinal, one can explicitly define an injection
![]() $g:\alpha \to A$
.
$g:\alpha \to A$
.
Proof See [Reference Shen12, Lemma 3.3].
The main idea of the following proof is originally from [Reference Halbeisen and Shelah5, Theorem 3].
Lemma 4.6. From an injection
![]() $f:\alpha \to \operatorname {fin}(A)$
, where
$f:\alpha \to \operatorname {fin}(A)$
, where
![]() $\alpha $
is an infinite ordinal, one can explicitly define an injection
$\alpha $
is an infinite ordinal, one can explicitly define an injection
![]() $h:\alpha \to \operatorname {fin}(A)$
such that the sets in
$h:\alpha \to \operatorname {fin}(A)$
such that the sets in
![]() ${\operatorname {ran}}(h)$
are pairwise disjoint and contain at least two elements.
${\operatorname {ran}}(h)$
are pairwise disjoint and contain at least two elements.
Proof Let f be an injection from
![]() $\alpha $
into
$\alpha $
into
![]() $\operatorname {fin}(A)$
, where
$\operatorname {fin}(A)$
, where
![]() $\alpha $
is an infinite ordinal. Let
$\alpha $
is an infinite ordinal. Let
![]() $\sim $
be the equivalence relation on A defined by
$\sim $
be the equivalence relation on A defined by
Clearly, for every
![]() $x\in \bigcup {\operatorname {ran}}(f)$
, the equivalence class
$x\in \bigcup {\operatorname {ran}}(f)$
, the equivalence class
![]() $[x]_\sim $
is finite.
$[x]_\sim $
is finite.
We want to show that there are
![]() $\alpha $
many such equivalence classes. In order to prove this, define a function
$\alpha $
many such equivalence classes. In order to prove this, define a function
![]() $\Psi $
on
$\Psi $
on
![]() $\bigcup {\operatorname {ran}}(f)$
by
$\bigcup {\operatorname {ran}}(f)$
by
We claim that, for all
![]() $x,y\in \bigcup {\operatorname {ran}}(f)$
,
$x,y\in \bigcup {\operatorname {ran}}(f)$
,
Clearly, if
![]() $x\sim y$
then
$x\sim y$
then
![]() $\Psi (x)=\Psi (y)$
. For the other direction, assume towards a contradiction that
$\Psi (x)=\Psi (y)$
. For the other direction, assume towards a contradiction that
![]() $\Psi (x)=\Psi (y)$
but not
$\Psi (x)=\Psi (y)$
but not
![]() $x\sim y$
. Let
$x\sim y$
. Let
![]() $\delta <\alpha $
be the least ordinal such that
$\delta <\alpha $
be the least ordinal such that
![]() $x\in f(\delta )$
is not equivalent to
$x\in f(\delta )$
is not equivalent to
![]() $y\in f(\delta )$
. Without loss of generality, assume that
$y\in f(\delta )$
. Without loss of generality, assume that
![]() $x\in f(\delta )$
but
$x\in f(\delta )$
but
![]() $y\notin f(\delta )$
. Since
$y\notin f(\delta )$
. Since
![]() $y\notin f(\delta )$
, we have
$y\notin f(\delta )$
, we have
![]() $\delta \notin \Psi (y)=\Psi (x)$
, which implies that
$\delta \notin \Psi (y)=\Psi (x)$
, which implies that
![]() $\bigcap \{f(\beta )\mid \beta <\delta \text { and }x\in f(\beta )\}\subseteq f(\delta )$
. Since, for all
$\bigcap \{f(\beta )\mid \beta <\delta \text { and }x\in f(\beta )\}\subseteq f(\delta )$
. Since, for all
![]() $\beta <\delta $
,
$\beta <\delta $
,
![]() $x\in f(\beta )$
if and only if
$x\in f(\beta )$
if and only if
![]() $y\in f(\beta )$
, it follows that
$y\in f(\beta )$
, it follows that
![]() $y\in \bigcap \{f(\beta )\mid \beta <\delta \text { and }x\in f(\beta )\}\subseteq f(\delta )$
, which is a contradiction.
$y\in \bigcap \{f(\beta )\mid \beta <\delta \text { and }x\in f(\beta )\}\subseteq f(\delta )$
, which is a contradiction.
We also claim that, for all
![]() $x\in \bigcup {\operatorname {ran}}(f)$
,
$x\in \bigcup {\operatorname {ran}}(f)$
,
Let
![]() $\xi $
be the least ordinal such that
$\xi $
be the least ordinal such that
![]() $x\in f(\xi )$
. Then
$x\in f(\xi )$
. Then
![]() $\xi $
is the first element of
$\xi $
is the first element of
![]() $\Psi (x)$
. For all
$\Psi (x)$
. For all
![]() $\gamma ,\delta \in \Psi (x)$
with
$\gamma ,\delta \in \Psi (x)$
with
![]() $\gamma <\delta $
, if
$\gamma <\delta $
, if
![]() $f(\xi )\cap f(\gamma )=f(\xi )\cap f(\delta )$
, then
$f(\xi )\cap f(\gamma )=f(\xi )\cap f(\delta )$
, then
![]() $\bigcap \{f(\beta )\mid \beta <\delta \text { and }x\in f(\beta )\}\subseteq f(\xi )\cap f(\gamma )\subseteq f(\delta )$
, contradicting that
$\bigcap \{f(\beta )\mid \beta <\delta \text { and }x\in f(\beta )\}\subseteq f(\xi )\cap f(\gamma )\subseteq f(\delta )$
, contradicting that
![]() $\delta \in \Psi (x)$
. Hence, the function that maps each
$\delta \in \Psi (x)$
. Hence, the function that maps each
![]() $\gamma \in \Psi (x)$
to
$\gamma \in \Psi (x)$
to
![]() $f(\xi )\cap f(\gamma )$
is an injection from
$f(\xi )\cap f(\gamma )$
is an injection from
![]() $\Psi (x)$
into
$\Psi (x)$
into
![]() $\mathscr {P}(f(\xi ))$
. Since
$\mathscr {P}(f(\xi ))$
. Since
![]() $\mathscr {P}(f(\xi ))$
is finite, it follows that
$\mathscr {P}(f(\xi ))$
is finite, it follows that
![]() $\Psi (x)$
is finite.
$\Psi (x)$
is finite.
Now, by Lemma 4.4, we can explicitly define an injection
![]() $p:\operatorname {fin}(\alpha )\to \alpha $
. By (2),
$p:\operatorname {fin}(\alpha )\to \alpha $
. By (2),
![]() ${\operatorname {ran}}(\Psi )\subseteq \operatorname {fin}(\alpha )$
. Let R be the well-ordering of
${\operatorname {ran}}(\Psi )\subseteq \operatorname {fin}(\alpha )$
. Let R be the well-ordering of
![]() ${\operatorname {ran}}(\Psi )$
induced by p; that is,
${\operatorname {ran}}(\Psi )$
induced by p; that is,
![]() $R=\{(a,b)\mid a,b\in {\operatorname {ran}}(\Psi )\text { and }p(a)<p(b)\}$
. Let
$R=\{(a,b)\mid a,b\in {\operatorname {ran}}(\Psi )\text { and }p(a)<p(b)\}$
. Let
![]() $\theta $
be the order type of
$\theta $
be the order type of
![]() $\langle {\operatorname {ran}}(\Psi ),R\rangle$
, and let
$\langle {\operatorname {ran}}(\Psi ),R\rangle$
, and let
![]() $\Theta $
be the unique isomorphism of
$\Theta $
be the unique isomorphism of
![]() $\langle {\operatorname {ran}}(\Psi ),R\rangle$
onto
$\langle {\operatorname {ran}}(\Psi ),R\rangle$
onto
![]() $\langle \theta ,\in \rangle$
. It is easy to see that
$\langle \theta ,\in \rangle$
. It is easy to see that
![]() $\theta $
is an infinite ordinal.
$\theta $
is an infinite ordinal.
Again, by Lemma 4.4, we can explicitly define an injection
![]() $q:\operatorname {fin}(\theta )\to \theta $
. By (1), the function that maps each
$q:\operatorname {fin}(\theta )\to \theta $
. By (1), the function that maps each
![]() $\beta <\alpha $
to
$\beta <\alpha $
to
![]() $\Psi [f(\beta )]$
is an injection from
$\Psi [f(\beta )]$
is an injection from
![]() $\alpha $
into
$\alpha $
into
![]() $\operatorname {fin}({\operatorname {ran}}(\Psi ))$
. Let g be the function on
$\operatorname {fin}({\operatorname {ran}}(\Psi ))$
. Let g be the function on
![]() $\alpha $
defined by
$\alpha $
defined by
g is visualized by the following diagram:
Hence, g is an injection from
![]() $\alpha $
into
$\alpha $
into
![]() ${\operatorname {ran}}(\Psi )$
.
${\operatorname {ran}}(\Psi )$
.
By Lemma 4.3, we can explicitly define an injection
![]() $s:\alpha \times \alpha \to \alpha $
. Then the function h on
$s:\alpha \times \alpha \to \alpha $
. Then the function h on
![]() $\alpha $
defined by
$\alpha $
defined by
is the required function.
Corollary 4.7. From an injection
![]() $f:\alpha \to \operatorname {fin}(A)$
, where
$f:\alpha \to \operatorname {fin}(A)$
, where
![]() $\alpha $
is an infinite ordinal, one can explicitly define a surjection
$\alpha $
is an infinite ordinal, one can explicitly define a surjection
![]() $g:A\twoheadrightarrow \alpha $
and an auxiliary function for g.
$g:A\twoheadrightarrow \alpha $
and an auxiliary function for g.
Proof Let f be an injection from
![]() $\alpha $
into
$\alpha $
into
![]() $\operatorname {fin}(A)$
, where
$\operatorname {fin}(A)$
, where
![]() $\alpha $
is an infinite ordinal. By Lemma 4.6, we can explicitly define an injection
$\alpha $
is an infinite ordinal. By Lemma 4.6, we can explicitly define an injection
![]() $h:\alpha \to \operatorname {fin}(A)$
such that the sets in
$h:\alpha \to \operatorname {fin}(A)$
such that the sets in
![]() ${\operatorname {ran}}(h)$
are pairwise disjoint and contain at least two elements. Now, the function g on A defined by
${\operatorname {ran}}(h)$
are pairwise disjoint and contain at least two elements. Now, the function g on A defined by
 $$\begin{align*}g(x)= \begin{cases} \text{the unique }\beta<\alpha\text{ for which }x\in h(\beta), & \text{if}\ x\in\bigcup{\operatorname{ran}}(h),\\ 0, & \text{otherwise,} \end{cases} \end{align*}$$
$$\begin{align*}g(x)= \begin{cases} \text{the unique }\beta<\alpha\text{ for which }x\in h(\beta), & \text{if}\ x\in\bigcup{\operatorname{ran}}(h),\\ 0, & \text{otherwise,} \end{cases} \end{align*}$$
is a surjection from A onto
![]() $\alpha $
, and the function t on
$\alpha $
, and the function t on
![]() $\alpha $
defined by
$\alpha $
defined by
 $$\begin{align*}t(\beta)= \begin{cases} \{h(0)\}\cup\{\{x\}\mid x\in A\setminus\bigcup{\operatorname{ran}}(h)\}, & \text{if}\ \beta=0,\\ \{h(\beta)\}, & \text{otherwise,} \end{cases} \end{align*}$$
$$\begin{align*}t(\beta)= \begin{cases} \{h(0)\}\cup\{\{x\}\mid x\in A\setminus\bigcup{\operatorname{ran}}(h)\}, & \text{if}\ \beta=0,\\ \{h(\beta)\}, & \text{otherwise,} \end{cases} \end{align*}$$
is an auxiliary function for g.
Now we are ready to prove our main theorem.
Theorem 4.8. If
![]() $\mathscr {B}(A)$
is Dedekind infinite, then there are no Dedekind finite-to-one functions from
$\mathscr {B}(A)$
is Dedekind infinite, then there are no Dedekind finite-to-one functions from
![]() $\mathscr {B}(A)$
to
$\mathscr {B}(A)$
to
![]() $\operatorname {fin}(A)$
.
$\operatorname {fin}(A)$
.
Proof Assume towards a contradiction that
![]() $\mathscr {B}(A)$
is Dedekind infinite and there is a Dedekind finite-to-one function
$\mathscr {B}(A)$
is Dedekind infinite and there is a Dedekind finite-to-one function
![]() $\Phi :\mathscr {B}(A)\to \operatorname {fin}(A)$
. Let h be an injection from
$\Phi :\mathscr {B}(A)\to \operatorname {fin}(A)$
. Let h be an injection from
![]() $\omega $
into
$\omega $
into
![]() $\mathscr {B}(A)$
. In what follows, we get a contradiction by constructing by recursion an injection H from the proper class of ordinals into the set
$\mathscr {B}(A)$
. In what follows, we get a contradiction by constructing by recursion an injection H from the proper class of ordinals into the set
![]() $\mathscr {B}(A)$
.
$\mathscr {B}(A)$
.
For
![]() $n\in \omega $
, take
$n\in \omega $
, take
![]() $H(n)=h(n)$
. Now, we assume that
$H(n)=h(n)$
. Now, we assume that
![]() $\alpha $
is an infinite ordinal and
$\alpha $
is an infinite ordinal and
![]() $H{\upharpoonright }\alpha $
is an injection from
$H{\upharpoonright }\alpha $
is an injection from
![]() $\alpha $
into
$\alpha $
into
![]() $\mathscr {B}(A)$
. Then
$\mathscr {B}(A)$
. Then
![]() $\Phi \circ (H{\upharpoonright }\alpha )$
is a Dedekind finite-to-one function from
$\Phi \circ (H{\upharpoonright }\alpha )$
is a Dedekind finite-to-one function from
![]() $\alpha $
to
$\alpha $
to
![]() $\operatorname {fin}(A)$
. Since all Dedekind finite subsets of
$\operatorname {fin}(A)$
. Since all Dedekind finite subsets of
![]() $\alpha $
are finite,
$\alpha $
are finite,
![]() $\Phi \circ (H{\upharpoonright }\alpha )$
is finite-to-one. By Lemma 4.5,
$\Phi \circ (H{\upharpoonright }\alpha )$
is finite-to-one. By Lemma 4.5,
![]() $\Phi \circ (H{\upharpoonright }\alpha )$
explicitly provides an injection
$\Phi \circ (H{\upharpoonright }\alpha )$
explicitly provides an injection
![]() $f:\alpha \to \operatorname {fin}(A)$
. Therefore, by Corollary 4.7, from f, we can explicitly define a surjection
$f:\alpha \to \operatorname {fin}(A)$
. Therefore, by Corollary 4.7, from f, we can explicitly define a surjection
![]() $g:A\twoheadrightarrow \alpha $
and an auxiliary function t for g. Then
$g:A\twoheadrightarrow \alpha $
and an auxiliary function t for g. Then
![]() $(H{\upharpoonright }\alpha )\circ g$
is a surjection from A onto
$(H{\upharpoonright }\alpha )\circ g$
is a surjection from A onto
![]() $H[\alpha ]$
and
$H[\alpha ]$
and
![]() $t\circ (H{\upharpoonright }\alpha )^{-1}$
is an auxiliary function for
$t\circ (H{\upharpoonright }\alpha )^{-1}$
is an auxiliary function for
![]() $(H{\upharpoonright }\alpha )\circ g$
. Hence, it follows from Lemma 4.2 that we can explicitly define an
$(H{\upharpoonright }\alpha )\circ g$
. Hence, it follows from Lemma 4.2 that we can explicitly define an
![]() $H(\alpha )\in \mathscr {B}(A)\setminus H[\alpha ]$
from
$H(\alpha )\in \mathscr {B}(A)\setminus H[\alpha ]$
from
![]() $H{\upharpoonright }\alpha $
(and
$H{\upharpoonright }\alpha $
(and
![]() $\Phi $
).
$\Phi $
).
We draw some corollaries from the above theorem. The next two corollaries immediately follows from Theorem 4.8 and Facts 2.10, 2.11, and 2.17.
Corollary 4.9. If
![]() $\mathscr {B}(A)$
is Dedekind infinite, then there are no Dedekind finite-to-one functions from
$\mathscr {B}(A)$
is Dedekind infinite, then there are no Dedekind finite-to-one functions from
![]() $\mathscr {B}(A)$
to
$\mathscr {B}(A)$
to
![]() ${\operatorname {seq}^{1-1}}(A)$
.
${\operatorname {seq}^{1-1}}(A)$
.
Corollary 4.10. If
![]() $\mathscr {B}(A)$
is Dedekind infinite, then there are no Dedekind finite-to-one functions from
$\mathscr {B}(A)$
is Dedekind infinite, then there are no Dedekind finite-to-one functions from
![]() $\mathscr {B}(A)$
to
$\mathscr {B}(A)$
to
![]() ${\mathscr {B}_{\operatorname {fin}}}(A)$
, and thus
${\mathscr {B}_{\operatorname {fin}}}(A)$
, and thus
![]() $|\mathscr {B}_{\mathrm {fin}}(A)|<|\mathscr {B}(A)|$
.
$|\mathscr {B}_{\mathrm {fin}}(A)|<|\mathscr {B}(A)|$
.
Corollary 4.11. If
![]() $\mathscr {B}(A)\neq {\mathscr {B}_{\operatorname {fin}}}(A)$
, then
$\mathscr {B}(A)\neq {\mathscr {B}_{\operatorname {fin}}}(A)$
, then
![]() $|\mathscr {B}_{\mathrm {fin}}(A)|<|\mathscr {B}(A)|$
.
$|\mathscr {B}_{\mathrm {fin}}(A)|<|\mathscr {B}(A)|$
.
Proof Suppose
![]() $\mathscr {B}(A)\neq {\mathscr {B}_{\operatorname {fin}}}(A)$
. Clearly,
$\mathscr {B}(A)\neq {\mathscr {B}_{\operatorname {fin}}}(A)$
. Clearly,
![]() $|\mathscr {B}_{\mathrm {fin}}(A)|\leqslant |\mathscr {B}(A)|$
. If
$|\mathscr {B}_{\mathrm {fin}}(A)|\leqslant |\mathscr {B}(A)|$
. If
![]() $|\mathscr {B}(A)|=|\mathscr {B}_{\mathrm {fin}}(A)|$
, since
$|\mathscr {B}(A)|=|\mathscr {B}_{\mathrm {fin}}(A)|$
, since
![]() ${\mathscr {B}_{\operatorname {fin}}}(A)\subset \mathscr {B}(A)$
, it follows that
${\mathscr {B}_{\operatorname {fin}}}(A)\subset \mathscr {B}(A)$
, it follows that
![]() $\mathscr {B}(A)$
is Dedekind infinite, contradicting Corollary 4.10. Hence,
$\mathscr {B}(A)$
is Dedekind infinite, contradicting Corollary 4.10. Hence,
![]() $|\mathscr {B}_{\mathrm {fin}}(A)|<|\mathscr {B}(A)|$
.
$|\mathscr {B}_{\mathrm {fin}}(A)|<|\mathscr {B}(A)|$
.
The following corollary is also proved in [Reference Phansamdaeng and Vejjajiva10, Theorem 3.7].
Corollary 4.12. For all infinite sets A,
![]() $|\mathrm {fin}(A)|<|\mathscr {B}(A)|$
.
$|\mathrm {fin}(A)|<|\mathscr {B}(A)|$
.
Proof By Fact 2.19,
![]() $|\mathrm {fin}(A)|\leqslant |\mathscr {B}_{\mathrm {fin}}(A)|\leqslant |\mathscr {B}(A)|$
. If
$|\mathrm {fin}(A)|\leqslant |\mathscr {B}_{\mathrm {fin}}(A)|\leqslant |\mathscr {B}(A)|$
. If
![]() $|\mathscr {B}(A)|=|\mathrm {fin}(A)|$
, since the injection constructed in the proof of Fact 2.19 is not surjective, it follows that
$|\mathscr {B}(A)|=|\mathrm {fin}(A)|$
, since the injection constructed in the proof of Fact 2.19 is not surjective, it follows that
![]() $\mathscr {B}(A)$
is Dedekind infinite, contradicting Theorem 4.8. Thus,
$\mathscr {B}(A)$
is Dedekind infinite, contradicting Theorem 4.8. Thus,
![]() $|\mathrm {fin}(A)|<|\mathscr {B}(A)|$
.
$|\mathrm {fin}(A)|<|\mathscr {B}(A)|$
.
4.2
 $|\mathscr {B}(A)|\neq |\mathrm {seq}(A)|$
$|\mathscr {B}(A)|\neq |\mathrm {seq}(A)|$
We need the following result, which is a Kuratowski-like theorem for
![]() $\mathscr {B}(A)$
.
$\mathscr {B}(A)$
.
Theorem 4.13. For all sets A, the following are equivalent:
-
(i)
 $\mathscr {B}(A)$
is Dedekind infinite;
$\mathscr {B}(A)$
is Dedekind infinite; -
(ii)
 ${\operatorname {ns}}(P)$
is power Dedekind infinite for some
${\operatorname {ns}}(P)$
is power Dedekind infinite for some
 $P\in \mathscr {B}(A)$
;
$P\in \mathscr {B}(A)$
; -
(iii)
 $\mathscr {P}(\omega )\preccurlyeq \mathscr {B}(A)$
.
$\mathscr {P}(\omega )\preccurlyeq \mathscr {B}(A)$
.
Proof (i)
![]() ${}\Rightarrow {}$
(ii). Suppose that
${}\Rightarrow {}$
(ii). Suppose that
![]() $\mathscr {B}(A)$
is Dedekind infinite. Assume towards a contradiction that
$\mathscr {B}(A)$
is Dedekind infinite. Assume towards a contradiction that
![]() ${\operatorname {ns}}(P)$
is power Dedekind finite for all
${\operatorname {ns}}(P)$
is power Dedekind finite for all
![]() $P\in \mathscr {B}(A)$
. Let
$P\in \mathscr {B}(A)$
. Let
![]() $\langle P_k\mid k\in \omega \rangle$
be a denumerable family of finitary partitions of A. We define by recursion a sequence
$\langle P_k\mid k\in \omega \rangle$
be a denumerable family of finitary partitions of A. We define by recursion a sequence
![]() $\langle Q_n\mid n\in \omega \rangle$
of finitary partitions of A such that
$\langle Q_n\mid n\in \omega \rangle$
of finitary partitions of A such that
![]() ${\operatorname {ns}}(Q_j)\neq \varnothing $
and
${\operatorname {ns}}(Q_j)\neq \varnothing $
and
![]() $\bigcup {\operatorname {ns}}(Q_i)\cap \bigcup {\operatorname {ns}}(Q_j)=\varnothing $
whenever
$\bigcup {\operatorname {ns}}(Q_i)\cap \bigcup {\operatorname {ns}}(Q_j)=\varnothing $
whenever
![]() $i\neq j$
as follows.
$i\neq j$
as follows.
Let
![]() $n\in \omega $
and assume that
$n\in \omega $
and assume that
![]() $Q_i$
has already been defined for all
$Q_i$
has already been defined for all
![]() $i<n$
. Let
$i<n$
. Let
![]() $B=\bigcup _{i<n}\bigcup {\operatorname {ns}}(Q_i)$
. By assumption,
$B=\bigcup _{i<n}\bigcup {\operatorname {ns}}(Q_i)$
. By assumption,
![]() ${\operatorname {ns}}(Q_i)$
is power Dedekind finite, so is
${\operatorname {ns}}(Q_i)$
is power Dedekind finite, so is
![]() $\bigcup {\operatorname {ns}}(Q_i)$
by Fact 2.5. Hence, B is power Dedekind finite. Consider the following two cases:
$\bigcup {\operatorname {ns}}(Q_i)$
by Fact 2.5. Hence, B is power Dedekind finite. Consider the following two cases:
Case 1. For a least
![]() $k\in \omega $
,
$k\in \omega $
,
![]() $x\sim _{P_k}y$
for some distinct
$x\sim _{P_k}y$
for some distinct
![]() $x,y\in A\setminus B$
. Then we define
$x,y\in A\setminus B$
. Then we define
It is easy to see that
![]() $Q_n$
is a finitary partition of A such that
$Q_n$
is a finitary partition of A such that
![]() ${\operatorname {ns}}(Q_n)\neq \varnothing $
and
${\operatorname {ns}}(Q_n)\neq \varnothing $
and
![]() $\bigcup {\operatorname {ns}}(Q_i)\cap \bigcup {\operatorname {ns}}(Q_n)=\varnothing $
for all
$\bigcup {\operatorname {ns}}(Q_i)\cap \bigcup {\operatorname {ns}}(Q_n)=\varnothing $
for all
![]() $i<n$
.
$i<n$
.
Case 2. Otherwise. Then, for all
![]() $k\in \omega $
and all
$k\in \omega $
and all
![]() $x\in \bigcup {\operatorname {ns}}(P_k)\setminus B$
,
$x\in \bigcup {\operatorname {ns}}(P_k)\setminus B$
,
Define by recursion a sequence
![]() $\langle k_m\mid m\in \omega \rangle$
of natural numbers as follows.
$\langle k_m\mid m\in \omega \rangle$
of natural numbers as follows.
Let
![]() $m\in \omega $
and assume that
$m\in \omega $
and assume that
![]() $k_j$
has been defined for
$k_j$
has been defined for
![]() $j<m$
. By assumption,
$j<m$
. By assumption,
![]() ${\operatorname {ns}}(P_{k_j})$
is power Dedekind finite, so is
${\operatorname {ns}}(P_{k_j})$
is power Dedekind finite, so is
![]() $\bigcup {\operatorname {ns}}(P_{k_j})$
by Fact 2.5. Therefore,
$\bigcup {\operatorname {ns}}(P_{k_j})$
by Fact 2.5. Therefore,
![]() ${B\cup \bigcup _{j<m}\bigcup {\operatorname {ns}}(P_{k_j})}$
is power Dedekind finite. Hence, there is a
${B\cup \bigcup _{j<m}\bigcup {\operatorname {ns}}(P_{k_j})}$
is power Dedekind finite. Hence, there is a
![]() $k\in \omega $
such that
$k\in \omega $
such that
![]() ${\operatorname {ns}}(P_k)\nsubseteq\mathscr {P}(B\cup \bigcup _{j<m}\bigcup {\operatorname {ns}}(P_{k_j}))$
. Define
${\operatorname {ns}}(P_k)\nsubseteq\mathscr {P}(B\cup \bigcup _{j<m}\bigcup {\operatorname {ns}}(P_{k_j}))$
. Define
![]() $k_m$
to be the least such k. Then
$k_m$
to be the least such k. Then
Let f and g be the functions on
![]() $\omega $
defined by
$\omega $
defined by
 $$ \begin{align*} f(m) & ={\textstyle\bigcup}{\operatorname{ns}}(P_{k_m})\setminus\bigl(B\cup\bigcup_{j<m}{\textstyle\bigcup}{\operatorname{ns}}(P_{k_j})\bigr),\\ g(m) & =\{[x]_{P_{k_m}}\cap B\mid x\in f(m)\}. \end{align*} $$
$$ \begin{align*} f(m) & ={\textstyle\bigcup}{\operatorname{ns}}(P_{k_m})\setminus\bigl(B\cup\bigcup_{j<m}{\textstyle\bigcup}{\operatorname{ns}}(P_{k_j})\bigr),\\ g(m) & =\{[x]_{P_{k_m}}\cap B\mid x\in f(m)\}. \end{align*} $$
By (3), for every
![]() $m\in \omega $
,
$m\in \omega $
,
![]() $g(m)$
is a finitary partition of a subset of B, and hence
$g(m)$
is a finitary partition of a subset of B, and hence
![]() $\sim _{g(m)}$
is an element of
$\sim _{g(m)}$
is an element of
![]() $\mathscr {P}(B^2)$
. Since
$\mathscr {P}(B^2)$
. Since
![]() $\mathscr {P}(B^2)$
is Dedekind finite by Fact 2.6, there are least
$\mathscr {P}(B^2)$
is Dedekind finite by Fact 2.6, there are least
![]() $l_0,l_1\in \omega $
with
$l_0,l_1\in \omega $
with
![]() $l_0<l_1$
such that
$l_0<l_1$
such that
![]() ${\sim _{g(l_0)}}={\sim _{g(l_1)}}$
, and thus
${\sim _{g(l_0)}}={\sim _{g(l_1)}}$
, and thus
![]() $g(l_0)=g(l_1)$
. Let
$g(l_0)=g(l_1)$
. Let
Since
![]() $l_0<l_1$
,
$l_0<l_1$
,
![]() $f(l_0)\cap f(l_1)=\varnothing $
, and thus, by (3), the sets in D are pairwise disjoint. By (4),
$f(l_0)\cap f(l_1)=\varnothing $
, and thus, by (3), the sets in D are pairwise disjoint. By (4),
![]() $f(m)\neq \varnothing $
for all
$f(m)\neq \varnothing $
for all
![]() $m\in \omega $
, and since
$m\in \omega $
, and since
![]() $g(l_0)=g(l_1)$
, it follows that
$g(l_0)=g(l_1)$
, it follows that
![]() $D\neq \varnothing $
. Now, we define
$D\neq \varnothing $
. Now, we define
Then
![]() $Q_n$
is a finitary partition of A such that
$Q_n$
is a finitary partition of A such that
![]() ${\operatorname {ns}}(Q_n)=D\neq \varnothing $
; since
${\operatorname {ns}}(Q_n)=D\neq \varnothing $
; since
![]() $B\cap \bigcup D=\varnothing $
, it follows that
$B\cap \bigcup D=\varnothing $
, it follows that
![]() $\bigcup {\operatorname {ns}}(Q_i)\cap \bigcup {\operatorname {ns}}(Q_n)=\varnothing $
for all
$\bigcup {\operatorname {ns}}(Q_i)\cap \bigcup {\operatorname {ns}}(Q_n)=\varnothing $
for all
![]() $i<n$
.
$i<n$
.
Finally,
is a finitary partition of A such that
![]() ${\operatorname {ns}}(Q)=\bigcup _{n\in \omega }{\operatorname {ns}}(Q_n)$
is power Dedekind infinite, which is a contradiction.
${\operatorname {ns}}(Q)=\bigcup _{n\in \omega }{\operatorname {ns}}(Q_n)$
is power Dedekind infinite, which is a contradiction.
(ii)
![]() ${}\Rightarrow {}$
(iii). Suppose that P is a finitary partition of A such that
${}\Rightarrow {}$
(iii). Suppose that P is a finitary partition of A such that
![]() ${\operatorname {ns}}(P)$
is power Dedekind infinite. Let p be a surjection from
${\operatorname {ns}}(P)$
is power Dedekind infinite. Let p be a surjection from
![]() ${\operatorname {ns}}(P)$
onto
${\operatorname {ns}}(P)$
onto
![]() $\omega $
. Then the function h on
$\omega $
. Then the function h on
![]() $\mathscr {P}(\omega )$
defined by
$\mathscr {P}(\omega )$
defined by
is an injection from
![]() $\mathscr {P}(\omega )$
into
$\mathscr {P}(\omega )$
into
![]() $\mathscr {B}(A)$
.
$\mathscr {B}(A)$
.
(iii)
![]() ${}\Rightarrow {}$
(i). Obviously.
${}\Rightarrow {}$
(i). Obviously.
Corollary 4.14. If
![]() $\mathscr {B}(A)$
is Dedekind infinite, then there are no Dedekind finite-to-one functions from
$\mathscr {B}(A)$
is Dedekind infinite, then there are no Dedekind finite-to-one functions from
![]() $\mathscr {B}(A)$
to
$\mathscr {B}(A)$
to
![]() ${\operatorname {seq}}(A)$
.
${\operatorname {seq}}(A)$
.
Proof Assume towards a contradiction that
![]() $\mathscr {B}(A)$
is Dedekind infinite and there exists a Dedekind finite-to-one function from
$\mathscr {B}(A)$
is Dedekind infinite and there exists a Dedekind finite-to-one function from
![]() $\mathscr {B}(A)$
to
$\mathscr {B}(A)$
to
![]() ${\operatorname {seq}}(A)$
. If A is Dedekind infinite, then
${\operatorname {seq}}(A)$
. If A is Dedekind infinite, then
![]() ${\operatorname {seq}}(A)\approx {\operatorname {seq}^{1-1}}(A)$
by Fact 2.14, contradicting Corollary 4.9. Otherwise, by Fact 2.13, there is a Dedekind finite-to-one function from
${\operatorname {seq}}(A)\approx {\operatorname {seq}^{1-1}}(A)$
by Fact 2.14, contradicting Corollary 4.9. Otherwise, by Fact 2.13, there is a Dedekind finite-to-one function from
![]() ${\operatorname {seq}}(A)$
to
${\operatorname {seq}}(A)$
to
![]() $\omega $
. By Theorem 4.13,
$\omega $
. By Theorem 4.13,
![]() $\mathscr {B}(\omega )\approx \mathscr {P}(\omega )\preccurlyeq \mathscr {B}(A)$
, and therefore there is a Dedekind finite-to-one function from
$\mathscr {B}(\omega )\approx \mathscr {P}(\omega )\preccurlyeq \mathscr {B}(A)$
, and therefore there is a Dedekind finite-to-one function from
![]() $\mathscr {B}(\omega )$
to
$\mathscr {B}(\omega )$
to
![]() $\omega $
, contradicting again Corollary 4.9.
$\omega $
, contradicting again Corollary 4.9.
Corollary 4.15. For all non-empty sets A,
![]() $|\mathscr {B}(A)|\neq |\mathrm {seq}(A)|$
.
$|\mathscr {B}(A)|\neq |\mathrm {seq}(A)|$
.
Proof For all non-empty sets A, if
![]() $|\mathscr {B}(A)|=|\mathrm {seq}(A)|$
, then it follows from Fact 2.12 that
$|\mathscr {B}(A)|=|\mathrm {seq}(A)|$
, then it follows from Fact 2.12 that
![]() $\mathscr {B}(A)$
is Dedekind infinite, contradicting Corollary 4.14.
$\mathscr {B}(A)$
is Dedekind infinite, contradicting Corollary 4.14.
We do not know whether
![]() $|\mathscr {B}(A)|\neq |\mathrm {seq}^{\text {1-1}}(A)|$
for all infinite sets A is provable in
$|\mathscr {B}(A)|\neq |\mathrm {seq}^{\text {1-1}}(A)|$
for all infinite sets A is provable in
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
4.3
 $|A^n|<|\mathscr {B}(A)|$
$|A^n|<|\mathscr {B}(A)|$
The main idea of the following proof is originally from [Reference Truss20, Lemma (i)] (cf. also [Reference Shen14]).
Lemma 4.16. For all
![]() $n\in \omega $
, if
$n\in \omega $
, if
![]() $|A|\geqslant 2n(2^{n+1}-1)$
, then
$|A|\geqslant 2n(2^{n+1}-1)$
, then
![]() $|A^n|\leqslant |\mathscr {B}_{\mathrm {fin}}(A)|$
.
$|A^n|\leqslant |\mathscr {B}_{\mathrm {fin}}(A)|$
.
Proof Let
![]() $n\in \omega $
and let A be a set with at least
$n\in \omega $
and let A be a set with at least
![]() $2n(2^{n+1}-1)$
elements. Since
$2n(2^{n+1}-1)$
elements. Since
![]() $2^{i}=1+\sum _{k<i}2^k$
, we can choose
$2^{i}=1+\sum _{k<i}2^k$
, we can choose
![]() $2n(2^{n+1}-1)$
distinct elements of A so that they are divided into
$2n(2^{n+1}-1)$
distinct elements of A so that they are divided into
![]() $n+1$
sets
$n+1$
sets
![]() $H_i$
(
$H_i$
(
![]() $i\leqslant n$
) with
$i\leqslant n$
) with
We construct an injection f from
![]() $A^n$
into
$A^n$
into
![]() ${\mathscr {B}_{\operatorname {fin}}}(A)$
as follows. Without loss of generality, assume that
${\mathscr {B}_{\operatorname {fin}}}(A)$
as follows. Without loss of generality, assume that
![]() $A\cap \omega =\varnothing $
.
$A\cap \omega =\varnothing $
.
Let
![]() $s\in A^n$
. Let
$s\in A^n$
. Let
![]() $i_s$
be the least
$i_s$
be the least
![]() $i\leqslant n$
for which
$i\leqslant n$
for which
![]() $\mathrm {ran}(s)\cap H_i=\varnothing $
. There is such an i because
$\mathrm {ran}(s)\cap H_i=\varnothing $
. There is such an i because
![]() $|\mathrm {ran}(s)|\leqslant n$
. Let
$|\mathrm {ran}(s)|\leqslant n$
. Let
![]() $t_s$
be the function on n defined by
$t_s$
be the function on n defined by
 $$\begin{align*}t_s(j)= \begin{cases} s(j), & \text{if}\ s(j)\neq s(k)\ \text{for all}\ k<j,\\ \max\{k<j\mid s(j)=s(k)\}, & \text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}t_s(j)= \begin{cases} s(j), & \text{if}\ s(j)\neq s(k)\ \text{for all}\ k<j,\\ \max\{k<j\mid s(j)=s(k)\}, & \text{otherwise.} \end{cases} \end{align*}$$
Clearly,
![]() $t_s\in {\operatorname {seq}^{1-1}}(A\cup n)$
. Let
$t_s\in {\operatorname {seq}^{1-1}}(A\cup n)$
. Let
![]() $u_s$
be the function on n defined by
$u_s$
be the function on n defined by
 $$\begin{align*}u_s(j)= \begin{cases} a_{i_s,n+t_s(j)}, & \text{if}\ t_s(j)\in n,\\ b_{i_s,t_s(j)}, & \text{if}\ t_s(j)\in H_k\ \text{for some}\ k<i_s,\\ t_s(j), & \text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}u_s(j)= \begin{cases} a_{i_s,n+t_s(j)}, & \text{if}\ t_s(j)\in n,\\ b_{i_s,t_s(j)}, & \text{if}\ t_s(j)\in H_k\ \text{for some}\ k<i_s,\\ t_s(j), & \text{otherwise.} \end{cases} \end{align*}$$
Then it is easy to see that
![]() $u_s\in {\operatorname {seq}^{1-1}}(A)$
. Now, we define
$u_s\in {\operatorname {seq}^{1-1}}(A)$
. Now, we define
Clearly,
![]() $f(s)\in {\mathscr {B}_{\operatorname {fin}}}(A)$
. We prove that f is injective by showing that s is uniquely determined by
$f(s)\in {\mathscr {B}_{\operatorname {fin}}}(A)$
. We prove that f is injective by showing that s is uniquely determined by
![]() $f(s)$
in the following way.
$f(s)$
in the following way.
First,
![]() $i_s$
is the least
$i_s$
is the least
![]() $i\leqslant n$
such that
$i\leqslant n$
such that
![]() $H_i\cap \bigcup {\operatorname {ns}}(f(s))\neq \varnothing $
. Second,
$H_i\cap \bigcup {\operatorname {ns}}(f(s))\neq \varnothing $
. Second,
![]() $u_s$
is the function on n such that
$u_s$
is the function on n such that
![]() $\{a_{i_s,j},u_s(j)\}\in f(s)$
for all
$\{a_{i_s,j},u_s(j)\}\in f(s)$
for all
![]() $j<n$
. Then,
$j<n$
. Then,
![]() $t_s$
is the function on n such that, for every
$t_s$
is the function on n such that, for every
![]() $j<n$
, either
$j<n$
, either
![]() $t_s(j)$
is the unique element of n for which
$t_s(j)$
is the unique element of n for which
![]() ${u_s(j)=a_{i_s,n+t_s(j)}}$
, or
${u_s(j)=a_{i_s,n+t_s(j)}}$
, or
![]() $t_s(j)$
is the unique element of
$t_s(j)$
is the unique element of
![]() $\bigcup _{k<i_s}H_k$
for which
$\bigcup _{k<i_s}H_k$
for which
![]() ${u_s(j)=b_{i_s,t_s(j)}}$
, or
${u_s(j)=b_{i_s,t_s(j)}}$
, or
![]() $t_s(j)=u_s(j)\notin H_{i_s}$
. Finally, s is the function on n recursively determined by
$t_s(j)=u_s(j)\notin H_{i_s}$
. Finally, s is the function on n recursively determined by
 $$\begin{align*}s(j)= \begin{cases} t_s(j), & \text{if}\ t_s(j)\in A,\\ s(t_s(j)), & \text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}s(j)= \begin{cases} t_s(j), & \text{if}\ t_s(j)\in A,\\ s(t_s(j)), & \text{otherwise.} \end{cases} \end{align*}$$
Hence, f is an injection from
![]() $A^n$
into
$A^n$
into
![]() ${\mathscr {B}_{\operatorname {fin}}}(A)$
.
${\mathscr {B}_{\operatorname {fin}}}(A)$
.
Corollary 4.17. For all
![]() $n\in \omega $
and all infinite sets A,
$n\in \omega $
and all infinite sets A,
![]() $|A^n|<|\mathscr {B}(A)|$
.
$|A^n|<|\mathscr {B}(A)|$
.
Proof By Lemma 4.16,
![]() $|A^n|\leqslant |\mathscr {B}_{\mathrm {fin}}(A)|\leqslant |\mathscr {B}(A)|$
. If
$|A^n|\leqslant |\mathscr {B}_{\mathrm {fin}}(A)|\leqslant |\mathscr {B}(A)|$
. If
![]() $|\mathscr {B}(A)|=|A^n|$
, since the injection constructed in the proof of Lemma 4.16 is not surjective,
$|\mathscr {B}(A)|=|A^n|$
, since the injection constructed in the proof of Lemma 4.16 is not surjective,
![]() $\mathscr {B}(A)$
is Dedekind infinite, contradicting Corollary 4.14. Thus,
$\mathscr {B}(A)$
is Dedekind infinite, contradicting Corollary 4.14. Thus,
![]() $|A^n|<|\mathscr {B}(A)|$
.
$|A^n|<|\mathscr {B}(A)|$
.
Lemma 4.18. If A is Dedekind infinite, then
![]() $|\mathrm {seq}(A)|\leqslant |\mathscr {B}_{\mathrm {fin}}(A)|$
.
$|\mathrm {seq}(A)|\leqslant |\mathscr {B}_{\mathrm {fin}}(A)|$
.
Proof Let h be an injection from
![]() $\omega $
into A. By the proof of Lemma 4.16, from
$\omega $
into A. By the proof of Lemma 4.16, from
![]() $h{\upharpoonright }(2n(2^{n+1}-1))$
, we can explicitly define an injection
$h{\upharpoonright }(2n(2^{n+1}-1))$
, we can explicitly define an injection
Then
![]() $\bigcup _{n\in \omega }f_n$
is an injection from
$\bigcup _{n\in \omega }f_n$
is an injection from
![]() ${\operatorname {seq}}(A)$
into
${\operatorname {seq}}(A)$
into
![]() ${\mathscr {B}_{\operatorname {fin}}}(A)$
.
${\mathscr {B}_{\operatorname {fin}}}(A)$
.
The following corollary immediately follows from Lemma 4.18 and Corollary 4.15.
Corollary 4.19. For all Dedekind infinite sets A,
![]() $|\mathrm {seq}(A)|<|\mathscr {B}(A)|$
.
$|\mathrm {seq}(A)|<|\mathscr {B}(A)|$
.
4.4 A Cantor-like theorem for
 $\mathscr {B}(A)$
$\mathscr {B}(A)$
Under the assumption that there is a finitary partition of A without singleton blocks, we show that Cantor’s theorem holds for
![]() $\mathscr {B}(A)$
. The key step of our proof is the following lemma.
$\mathscr {B}(A)$
. The key step of our proof is the following lemma.
Lemma 4.20. From a finitary partition P of A without singleton blocks and a surjection
![]() $f:A\twoheadrightarrow \alpha $
, where
$f:A\twoheadrightarrow \alpha $
, where
![]() $\alpha $
is an infinite ordinal, one can explicitly define a surjection
$\alpha $
is an infinite ordinal, one can explicitly define a surjection
![]() $g:A\twoheadrightarrow \alpha $
and an auxiliary function for g.
$g:A\twoheadrightarrow \alpha $
and an auxiliary function for g.
Proof Let P be a finitary partition of A without singleton blocks, and let f be a surjection from A onto
![]() $\alpha $
, where
$\alpha $
, where
![]() $\alpha $
is an infinite ordinal. Let
$\alpha $
is an infinite ordinal. Let
Clearly,
![]() $Q\subseteq \operatorname {fin}(\alpha )$
. By Lemma 4.4, we can explicitly define an injection
$Q\subseteq \operatorname {fin}(\alpha )$
. By Lemma 4.4, we can explicitly define an injection
![]() ${p:\mathrm {fin}(\alpha )\to \alpha} $
. Let R be the well-ordering of Q induced by p; that is,
${p:\mathrm {fin}(\alpha )\to \alpha} $
. Let R be the well-ordering of Q induced by p; that is,
![]() $R=\{(a,b)\mid a,b\in Q\text { and }p(a)<p(b)\}$
. Since P is a partition of A, Q is a cover of
$R=\{(a,b)\mid a,b\in Q\text { and }p(a)<p(b)\}$
. Since P is a partition of A, Q is a cover of
![]() $\alpha $
. Define a function h from
$\alpha $
. Define a function h from
![]() $\alpha $
to Q by setting, for
$\alpha $
to Q by setting, for
![]() $\beta \in \alpha $
,
$\beta \in \alpha $
,
Since
![]() $\beta \in h(\beta )$
and
$\beta \in h(\beta )$
and
![]() $h(\beta )$
is finite for all
$h(\beta )$
is finite for all
![]() $\beta \in \alpha $
, h is a finite-to-one function from
$\beta \in \alpha $
, h is a finite-to-one function from
![]() $\alpha $
to Q. Hence, by Lemma 4.5, h explicitly provides an injection from
$\alpha $
to Q. Hence, by Lemma 4.5, h explicitly provides an injection from
![]() $\alpha $
into Q. Since
$\alpha $
into Q. Since
![]() $p{\upharpoonright }Q$
is an injection from Q into
$p{\upharpoonright }Q$
is an injection from Q into
![]() $\alpha $
, it follows from Theorem 2.2 that we can explicitly define a bijection q between Q and
$\alpha $
, it follows from Theorem 2.2 that we can explicitly define a bijection q between Q and
![]() $\alpha $
.
$\alpha $
.
Now, the function g on A defined by
is a surjection from A onto
![]() $\alpha $
, and the function t on
$\alpha $
, and the function t on
![]() $\alpha $
defined by
$\alpha $
defined by
is an auxiliary function for g.
Theorem 4.21. For all infinite sets A, if there is a finitary partition of A without singleton blocks, then there are no surjections from A onto
![]() $\mathscr {B}(A)$
.
$\mathscr {B}(A)$
.
Proof Let A be an infinite set and let P be a finitary partition of A without singleton blocks. Assume towards a contradiction that there is a surjection
![]() ${\Phi :A\twoheadrightarrow \mathscr {B}(A)}$
. By Corollary 2.20,
${\Phi :A\twoheadrightarrow \mathscr {B}(A)}$
. By Corollary 2.20,
![]() $\mathscr {B}(A)$
is power Dedekind infinite, so is A. Since
$\mathscr {B}(A)$
is power Dedekind infinite, so is A. Since
![]() $\bigcup {\operatorname {ns}}(P)=A$
is power Dedekind infinite, so is
$\bigcup {\operatorname {ns}}(P)=A$
is power Dedekind infinite, so is
![]() ${\operatorname {ns}}(P)$
by Fact 2.5. Hence, by Theorem 4.13,
${\operatorname {ns}}(P)$
by Fact 2.5. Hence, by Theorem 4.13,
![]() $\mathscr {B}(A)$
is Dedekind infinite. Let h be an injection from
$\mathscr {B}(A)$
is Dedekind infinite. Let h be an injection from
![]() $\omega $
into
$\omega $
into
![]() $\mathscr {B}(A)$
. In what follows, we get a contradiction by constructing by recursion an injection H from the proper class of ordinals into
$\mathscr {B}(A)$
. In what follows, we get a contradiction by constructing by recursion an injection H from the proper class of ordinals into
![]() $\mathscr {B}(A)$
.
$\mathscr {B}(A)$
.
For
![]() $n\in \omega $
, take
$n\in \omega $
, take
![]() $H(n)=h(n)$
. Now, we assume that
$H(n)=h(n)$
. Now, we assume that
![]() $\alpha $
is an infinite ordinal and
$\alpha $
is an infinite ordinal and
![]() $H{\upharpoonright }\alpha $
is an injection from
$H{\upharpoonright }\alpha $
is an injection from
![]() $\alpha $
into
$\alpha $
into
![]() $\mathscr {B}(A)$
. Then
$\mathscr {B}(A)$
. Then
![]() $(H{\upharpoonright }\alpha )^{-1}\circ \Phi $
is a surjection from a subset of A onto
$(H{\upharpoonright }\alpha )^{-1}\circ \Phi $
is a surjection from a subset of A onto
![]() $\alpha $
and thus can be extended by zero to a surjection
$\alpha $
and thus can be extended by zero to a surjection
![]() $f:A\twoheadrightarrow \alpha $
. By Lemma 4.20, from P and f, we can explicitly define a surjection
$f:A\twoheadrightarrow \alpha $
. By Lemma 4.20, from P and f, we can explicitly define a surjection
![]() $g:A\twoheadrightarrow \alpha $
and an auxiliary function t for g. Then
$g:A\twoheadrightarrow \alpha $
and an auxiliary function t for g. Then
![]() $(H{\upharpoonright }\alpha )\circ g$
is a surjection from A onto
$(H{\upharpoonright }\alpha )\circ g$
is a surjection from A onto
![]() $H[\alpha ]$
and
$H[\alpha ]$
and
![]() $t\circ (H{\upharpoonright }\alpha )^{-1}$
is an auxiliary function for
$t\circ (H{\upharpoonright }\alpha )^{-1}$
is an auxiliary function for
![]() $(H{\upharpoonright }\alpha )\circ g$
. Hence, it follows from Lemma 4.2 that we can explicitly define an
$(H{\upharpoonright }\alpha )\circ g$
. Hence, it follows from Lemma 4.2 that we can explicitly define an
![]() $H(\alpha )\in \mathscr {B}(A)\setminus H[\alpha ]$
from
$H(\alpha )\in \mathscr {B}(A)\setminus H[\alpha ]$
from
![]() $H{\upharpoonright }\alpha $
(and
$H{\upharpoonright }\alpha $
(and
![]() $P,\Phi $
).
$P,\Phi $
).
Under the same assumption, we also show that there are no finite-to-one functions from
![]() $\mathscr {B}(A)$
to
$\mathscr {B}(A)$
to
![]() $A^n$
.
$A^n$
.
Theorem 4.22. For all infinite sets A, if there is a finitary partition of A without singleton blocks, then there are no finite-to-one functions from
![]() $\mathscr {B}(A)$
to
$\mathscr {B}(A)$
to
![]() $A^n$
for every
$A^n$
for every
![]() $n\in \omega $
.
$n\in \omega $
.
Proof Let A be an infinite set and let P be a finitary partition of A without singleton blocks. Assume towards a contradiction that there is a finite-to-one function from
![]() $\mathscr {B}(A)$
to
$\mathscr {B}(A)$
to
![]() $A^n$
for some
$A^n$
for some
![]() $n\in \omega $
. By Corollary 2.20,
$n\in \omega $
. By Corollary 2.20,
![]() $\mathscr {B}(A)$
is power Dedekind infinite, so is A by Facts 2.5 and 2.6. Since
$\mathscr {B}(A)$
is power Dedekind infinite, so is A by Facts 2.5 and 2.6. Since
![]() $\bigcup {\operatorname {ns}}(P)=A$
is power Dedekind infinite, so is
$\bigcup {\operatorname {ns}}(P)=A$
is power Dedekind infinite, so is
![]() ${\operatorname {ns}}(P)$
by Fact 2.5. Hence, by Theorem 4.13,
${\operatorname {ns}}(P)$
by Fact 2.5. Hence, by Theorem 4.13,
![]() $\mathscr {B}(A)$
is Dedekind infinite, contradicting Corollary 4.14.
$\mathscr {B}(A)$
is Dedekind infinite, contradicting Corollary 4.14.
4.5 The inequalities
 $|\mathscr {B}_{\mathrm {fin}}(A)|<|\mathrm {Part}_{\mathrm {fin}}(A)|$
and
$|\mathscr {B}_{\mathrm {fin}}(A)|<|\mathrm {Part}_{\mathrm {fin}}(A)|$
and
 $|\mathscr {B}_{\mathrm {fin}}(A)|\neq |\mathscr {P}(A)|$
$|\mathscr {B}_{\mathrm {fin}}(A)|\neq |\mathscr {P}(A)|$
Lemma 4.23. If A is power Dedekind infinite, then there are no finite-to-one functions from
![]() $\mathscr {P}(A)$
to
$\mathscr {P}(A)$
to
![]() $\operatorname {fin}(A)$
.
$\operatorname {fin}(A)$
.
Proof See [Reference Shen12, Corollary 3.7].
The next corollary immediately follows from Lemma 4.23 and Facts 2.11 and 2.17.
Corollary 4.24. If A is power Dedekind infinite, then there are no finite-to-one functions from
![]() $\mathscr {P}(A)$
to
$\mathscr {P}(A)$
to
![]() ${\mathscr {B}_{\operatorname {fin}}}(A)$
.
${\mathscr {B}_{\operatorname {fin}}}(A)$
.
Theorem 4.25. For all infinite sets A,
![]() $|\mathscr {B}_{\mathrm {fin}}(A)|<|\mathrm {Part}_{\mathrm {fin}}(A)|$
.
$|\mathscr {B}_{\mathrm {fin}}(A)|<|\mathrm {Part}_{\mathrm {fin}}(A)|$
.
Proof Let A be an infinite set. By Fact 2.18,
![]() $|\mathscr {B}_{\mathrm {fin}}(A)|\leqslant |\mathrm {Part}_{\mathrm {fin}}(A)|$
. Assume
$|\mathscr {B}_{\mathrm {fin}}(A)|\leqslant |\mathrm {Part}_{\mathrm {fin}}(A)|$
. Assume
![]() $|\mathrm {Part}_{\mathrm {fin}}(A)|=|\mathscr {B}_{\mathrm {fin}}(A)|$
. Since the injection constructed in the proof of Fact 2.18 is not surjective,
$|\mathrm {Part}_{\mathrm {fin}}(A)|=|\mathscr {B}_{\mathrm {fin}}(A)|$
. Since the injection constructed in the proof of Fact 2.18 is not surjective,
![]() ${\operatorname {Part}_{\operatorname {fin}}}(A)$
is Dedekind infinite, and thus A is power Dedekind infinite by Corollary 2.16. Now, by Fact 2.19,
${\operatorname {Part}_{\operatorname {fin}}}(A)$
is Dedekind infinite, and thus A is power Dedekind infinite by Corollary 2.16. Now, by Fact 2.19,
![]() $|\mathscr {P}(A)|\leqslant |\mathrm {Part}_{\mathrm {fin}}(A)|=|\mathscr {B}_{\mathrm {fin}}(A)|$
, contradicting Corollary 4.24. Hence,
$|\mathscr {P}(A)|\leqslant |\mathrm {Part}_{\mathrm {fin}}(A)|=|\mathscr {B}_{\mathrm {fin}}(A)|$
, contradicting Corollary 4.24. Hence,
![]() $|\mathscr {B}_{\mathrm {fin}}(A)|<|\mathrm {Part}_{\mathrm {fin}}(A)|$
.
$|\mathscr {B}_{\mathrm {fin}}(A)|<|\mathrm {Part}_{\mathrm {fin}}(A)|$
.
Finally, we prove
![]() $|\mathscr {B}_{\mathrm {fin}}(A)|\neq |\mathscr {P}(A)|$
. For this, we need the following number-theoretic lemma.
$|\mathscr {B}_{\mathrm {fin}}(A)|\neq |\mathscr {P}(A)|$
. For this, we need the following number-theoretic lemma.
Lemma 4.26. For each
![]() $n\in \omega $
, let
$n\in \omega $
, let
![]() $B_n$
be the nth Bell number; that is,
$B_n$
be the nth Bell number; that is,
![]() $B_n=|\mathscr {B}(n)|$
. Then
$B_n=|\mathscr {B}(n)|$
. Then
![]() $B_m$
is not a power of
$B_m$
is not a power of
![]() $2$
for all
$2$
for all
![]() $m\geqslant 3$
.
$m\geqslant 3$
.
Proof Let
![]() $m\geqslant 3$
. Then
$m\geqslant 3$
. Then
![]() $B_m>4$
. It suffices to prove that
$B_m>4$
. It suffices to prove that
![]() $B_m$
is not divisible by
$B_m$
is not divisible by
![]() $8$
. By [Reference Lunnon, Pleasants and Stephens7, Theorem 6.4],
$8$
. By [Reference Lunnon, Pleasants and Stephens7, Theorem 6.4],
![]() $B_{n+24}\equiv B_n\pmod {8}$
for all
$B_{n+24}\equiv B_n\pmod {8}$
for all
![]() $n\in \omega $
. But
$n\in \omega $
. But
![]() $B_n$
modulo
$B_n$
modulo
![]() $8$
for n from
$8$
for n from
![]() $0$
to
$0$
to
![]() $23$
are
$23$
are
Hence,
![]() $B_m$
is not divisible by
$B_m$
is not divisible by
![]() $8$
.
$8$
.
Lemma 4.27. If
![]() $\operatorname {fin}(\mathscr {P}(A))$
is Dedekind infinite, then A is power Dedekind infinite.
$\operatorname {fin}(\mathscr {P}(A))$
is Dedekind infinite, then A is power Dedekind infinite.
Proof See [Reference Shen13, Theorem 3.2].
Theorem 4.28. For all non-empty sets A,
![]() $|\mathscr {P}(A)|\neq |\mathscr {B}_{\mathrm {fin}}(A)|$
.
$|\mathscr {P}(A)|\neq |\mathscr {B}_{\mathrm {fin}}(A)|$
.
Proof If A is a singleton,
![]() $|\mathscr {P}(A)|=2\neq 1=|\mathscr {B}_{\mathrm {fin}}(A)|$
. Suppose
$|\mathscr {P}(A)|=2\neq 1=|\mathscr {B}_{\mathrm {fin}}(A)|$
. Suppose
![]() $|A|\geqslant 2$
, and fix two distinct elements
$|A|\geqslant 2$
, and fix two distinct elements
![]() $a,b$
of A. Assume toward a contradiction that there is a bijection
$a,b$
of A. Assume toward a contradiction that there is a bijection
![]() $\Phi $
between
$\Phi $
between
![]() $\mathscr {P}(A)$
and
$\mathscr {P}(A)$
and
![]() ${\mathscr {B}_{\operatorname {fin}}}(A)$
. We define by recursion an injection f from
${\mathscr {B}_{\operatorname {fin}}}(A)$
. We define by recursion an injection f from
![]() $\omega $
into
$\omega $
into
![]() $\operatorname {fin}(\mathscr {P}(A))$
as follows.
$\operatorname {fin}(\mathscr {P}(A))$
as follows.
Take
![]() $f(0)=\{\{a\},\{b\}\}$
. Let
$f(0)=\{\{a\},\{b\}\}$
. Let
![]() $n\in \omega $
, and assume that
$n\in \omega $
, and assume that
![]() $f(0),\dots ,f(n)$
have been defined and are pairwise distinct elements of
$f(0),\dots ,f(n)$
have been defined and are pairwise distinct elements of
![]() $\operatorname {fin}(\mathscr {P}(A))$
. Let
$\operatorname {fin}(\mathscr {P}(A))$
. Let
![]() $\sim $
be the equivalence relation on A defined by
$\sim $
be the equivalence relation on A defined by
Since
![]() $f(0),\dots ,f(n)$
are finite, the quotient set
$f(0),\dots ,f(n)$
are finite, the quotient set
![]() $A/{\sim }$
is a finite partition of A. Let
$A/{\sim }$
is a finite partition of A. Let
![]() $k=|A/{\sim }|$
and let
$k=|A/{\sim }|$
and let
![]() $U=\{\bigcup W\mid W\subseteq A/{\sim }\}$
. Then
$U=\{\bigcup W\mid W\subseteq A/{\sim }\}$
. Then
![]() $|U|=2^k$
and
$|U|=2^k$
and
Since
![]() $\{a\},\{b\}\in A/{\sim }$
, we have
$\{a\},\{b\}\in A/{\sim }$
, we have
![]() $k\geqslant 2$
. Let
$k\geqslant 2$
. Let
![]() $D=\bigcup \{\bigcup {\operatorname {ns}}(P)\mid P\in \Phi [U]\}$
. Since U is finite and
$D=\bigcup \{\bigcup {\operatorname {ns}}(P)\mid P\in \Phi [U]\}$
. Since U is finite and
![]() $\Phi [U]\subseteq {\mathscr {B}_{\operatorname {fin}}}(A)$
, it follows that D is finite. Let
$\Phi [U]\subseteq {\mathscr {B}_{\operatorname {fin}}}(A)$
, it follows that D is finite. Let
![]() $m=|D|$
and let
$m=|D|$
and let
![]() $E=\{P\in {\mathscr {B}_{\operatorname {fin}}}(A)\mid \bigcup {\operatorname {ns}}(P)\subseteq D\}$
. Then
$E=\{P\in {\mathscr {B}_{\operatorname {fin}}}(A)\mid \bigcup {\operatorname {ns}}(P)\subseteq D\}$
. Then
![]() $|E|=B_m$
and
$|E|=B_m$
and
![]() $\Phi [U]\subseteq E$
. Hence,
$\Phi [U]\subseteq E$
. Hence,
![]() $2^k=|U|=|\Phi [U]|\leqslant |E|=B_m$
. Since
$2^k=|U|=|\Phi [U]|\leqslant |E|=B_m$
. Since
![]() $k\geqslant 2$
, we have
$k\geqslant 2$
, we have
![]() $m\geqslant 3$
, which implies that
$m\geqslant 3$
, which implies that
![]() $B_m\neq 2^k$
by Lemma 4.26, and hence
$B_m\neq 2^k$
by Lemma 4.26, and hence
![]() $\Phi [U]\subset E$
. Now, we define
$\Phi [U]\subset E$
. Now, we define
![]() $f(n+1)=\Phi ^{-1}[E\setminus \Phi [U]]$
. Then
$f(n+1)=\Phi ^{-1}[E\setminus \Phi [U]]$
. Then
![]() $f(n+1)$
is a non-void finite subset of
$f(n+1)$
is a non-void finite subset of
![]() $\mathscr {P}(A)$
. By (5), it follows that
$\mathscr {P}(A)$
. By (5), it follows that
![]() $f(n+1)$
is disjoint from each of
$f(n+1)$
is disjoint from each of
![]() $f(0),\dots ,f(n)$
, and thus is distinct from each of them.
$f(0),\dots ,f(n)$
, and thus is distinct from each of them.
The existence of the above injection f shows that
![]() $\operatorname {fin}(\mathscr {P}(A))$
is Dedekind infinite, which implies that, by Lemma 4.27, A is power Dedekind infinite, contradicting Corollary 4.24.
$\operatorname {fin}(\mathscr {P}(A))$
is Dedekind infinite, which implies that, by Lemma 4.27, A is power Dedekind infinite, contradicting Corollary 4.24.
5 Open questions
We conclude the paper with the following five open questions.
Question 5.1. Are the following statements consistent with
![]() $\mathsf {ZF}$
?
$\mathsf {ZF}$
?
-
(1) There exist an infinite set A and a finite-to-one function from
 $\mathscr {B}(A)$
to A.
$\mathscr {B}(A)$
to A. -
(2) There exists an infinite set A for which
 $|\mathscr {B}(A)|<|\mathcal {S}_3(A)|$
, where
$|\mathscr {B}(A)|<|\mathcal {S}_3(A)|$
, where
 $\mathcal {S}_3(A)$
is the set of permutations of A with exactly three non-fixed points.
$\mathcal {S}_3(A)$
is the set of permutations of A with exactly three non-fixed points. -
(3) There exists an infinite set A for which
 $|\mathscr {B}(A)|=|\mathrm {seq}^{\text {1-1}}(A)|$
.
$|\mathscr {B}(A)|=|\mathrm {seq}^{\text {1-1}}(A)|$
. -
(4) There exists an infinite set A for which
 $|\mathrm {Part}_{\mathrm {fin}}(A)|<|\mathscr {B}(A)|$
.
$|\mathrm {Part}_{\mathrm {fin}}(A)|<|\mathscr {B}(A)|$
. -
(5) There exist an infinite set A and a surjection from
 $A^2$
onto
$A^2$
onto
 ${\operatorname {Part}}(A)$
.
${\operatorname {Part}}(A)$
.
Acknowledgements
I should like to give thanks to Professor Ira Gessel for providing a proof of Lemma 4.26.
Funding
The author was partially supported by the National Natural Science Foundation of China (Grant No. 12101466).