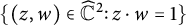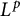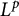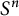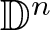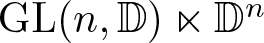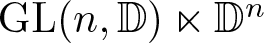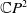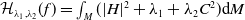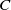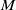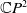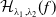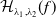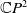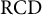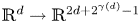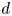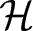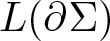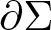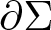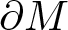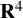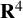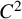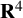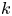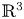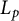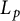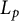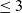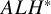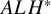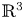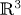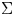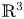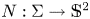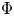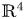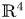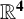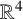102 results in 53Axx
Index estimates of compact hypersurfaces in smooth metric measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 March 2024, pp. 1-19
-
- Article
- Export citation
Spectral theory of the invariant Laplacian on the disk and the sphere – a complex analysis approach
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 01 March 2024, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Anisotropic flow, entropy, and
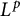 $L^p$-Minkowski problem
$L^p$-Minkowski problem
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reversibility of affine transformations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 08 November 2023, pp. 1217-1228
-
- Article
- Export citation
A Helfrich functional for compact surfaces in
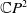 $\mathbb{C}P^{2}$
$\mathbb{C}P^{2}$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 04 October 2023, pp. 36-50
- Print publication:
- January 2024
-
- Article
- Export citation
A note about charts built by Eriksson-Bique and Soultanis on metric measure spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 09 June 2023, pp. 49-59
- Print publication:
- March 2024
-
- Article
- Export citation
On inscribed trapezoids and affinely 3-regular maps
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 12 May 2023, pp. 1-9
-
- Article
- Export citation
Total mean curvature surfaces in the product space
 ${\mathbb{S}^{n}\times\mathbb{R}}$ and applications
${\mathbb{S}^{n}\times\mathbb{R}}$ and applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 26 April 2023, pp. 346-365
-
- Article
- Export citation
Rigidity of capillary surfaces in compact 3-manifolds with strictly convex boundary
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 03 April 2023, pp. 231-240
-
- Article
- Export citation
Stable anisotropic minimal hypersurfaces in
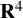 $\mathbf {R}^{4}$
$\mathbf {R}^{4}$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 02 February 2023, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On k-folding map-germs and hidden symmetries of surfaces in the Euclidean 3-space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 26 January 2023, pp. 60-104
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Curvature functionals on convex bodies
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 09 December 2022, pp. 761-779
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An improvement on Schmidt’s bound on the number of number fields of bounded discriminant and small degree
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 October 2022, e86
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Projective invariants of images
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 26 September 2022, pp. 936-946
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Torelli theorem for
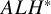 $ALH^*$
gravitational instantons
$ALH^*$
gravitational instantons
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 15 September 2022, e79
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonrigidity of flat ribbons
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 06 September 2022, pp. 1297-1314
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Surfaces of prescribed linear Weingarten curvature in $\mathbb {R}^{3}$
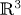
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 22 July 2022, pp. 1347-1370
- Print publication:
- August 2023
-
- Article
- Export citation
Singularities of 3-parameter line congruences in $\mathbb {R}^{4}$
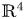
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 21 June 2022, pp. 1045-1070
- Print publication:
- June 2023
-
- Article
- Export citation
TRANSLATING SOLITONS FOR THE MEAN CURVATURE FLOW IN
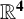 $\boldsymbol {{\mathbb {R}}^{4}}$
$\boldsymbol {{\mathbb {R}}^{4}}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 25 April 2022, pp. 491-499
- Print publication:
- December 2022
-
- Article
- Export citation
On complete submanifolds with parallel normalized mean curvature in product spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 27 January 2022, pp. 331-355
- Print publication:
- April 2022
-
- Article
- Export citation



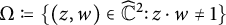 of the “complexified unit circle”
of the “complexified unit circle”