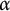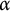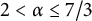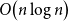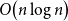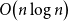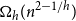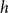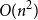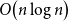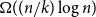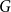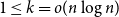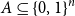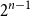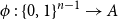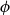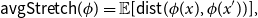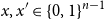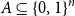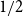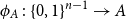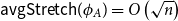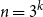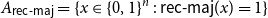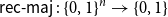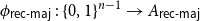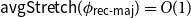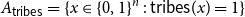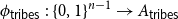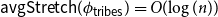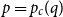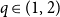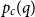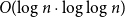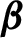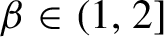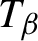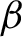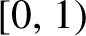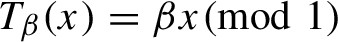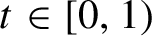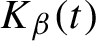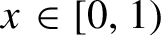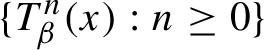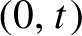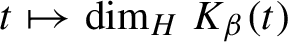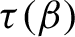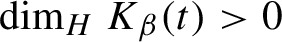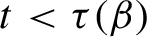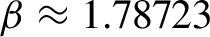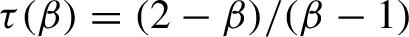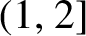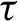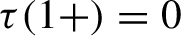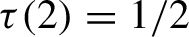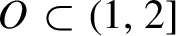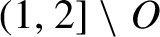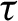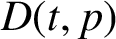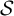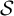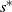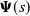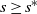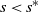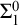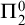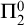77 results in 68Rxx
Indistinguishable asymptotic pairs and multidimensional Sturmian configurations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 31 May 2024, pp. 1-59
-
- Article
-
- You have access
- HTML
- Export citation
Bracket words along Hardy field sequences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 14 December 2023, pp. 2621-2648
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A word of low complexity without uniform frequencies
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1013-1025
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
The first-order theory of binary overlap-free words is decidable
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 26 May 2023, pp. 1144-1162
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Universal geometric graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 742-761
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mixing properties of erasing interval maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 06 March 2023, pp. 408-431
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
Multiple random walks on graphs: mixing few to cover many
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 15 February 2023, pp. 594-637
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On mappings on the hypercube with small average stretch
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 18 October 2022, pp. 334-348
-
- Article
-
- You have access
- HTML
- Export citation
The critical mean-field Chayes–Machta dynamics
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 11 May 2022, pp. 924-975
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Critical values for the
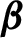 $\boldsymbol{\beta} $
-transformation with a hole at
$\boldsymbol{\beta} $
-transformation with a hole at
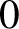 $0$
$0$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 02 May 2022, pp. 1785-1828
- Print publication:
- June 2023
-
- Article
-
- You have access
- HTML
- Export citation
SUBSHIFTS OF FINITE TYPE WITH A HOLE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 22 March 2022, pp. 73-98
- Print publication:
- August 2023
-
- Article
-
- You have access
- HTML
- Export citation
GAPS IN THE THUE–MORSE WORD
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 25 January 2022, pp. 110-144
- Print publication:
- February 2023
-
- Article
-
- You have access
- HTML
- Export citation
Tuning as convex optimisation: a polynomial tuner for multi-parametric combinatorial samplers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 15 December 2021, pp. 765-811
-
- Article
- Export citation
Sequential metric dimension for random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 909-951
- Print publication:
- December 2021
-
- Article
- Export citation
Clustering in preferential attachment random graphs with edge-step
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 890-908
- Print publication:
- December 2021
-
- Article
- Export citation
THE p-ZASSENHAUS FILTRATION OF A FREE PROFINITE GROUP AND SHUFFLE RELATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 961-983
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
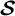 $\mathcal{\textbf{S}}$
-adic characterization of minimal ternary dendric shifts
$\mathcal{\textbf{S}}$
-adic characterization of minimal ternary dendric shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 02 September 2021, pp. 3393-3432
- Print publication:
- November 2022
-
- Article
- Export citation
Yaglom limit for stochastic fluid models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 649-686
- Print publication:
- September 2021
-
- Article
- Export citation
A MATHEMATICAL COMMITMENT WITHOUT COMPUTATIONAL STRENGTH
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 July 2021, pp. 880-906
- Print publication:
- December 2022
-
- Article
- Export citation
The power of two choices for random walks
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 28 May 2021, pp. 73-100
-
- Article
-
- You have access
- Open access
- Export citation