Article contents
Mixing properties of erasing interval maps
Published online by Cambridge University Press: 06 March 2023
Abstract
We study the measurable dynamical properties of the interval map generated by the model-case erasing substitution 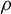 $\rho $, defined by
$\rho $, defined by 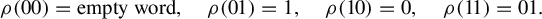 $$ \begin{align*} \rho(00)=\text{empty word},\quad \rho(01)=1,\quad \rho(10)=0,\quad \rho(11)=01. \end{align*} $$
$$ \begin{align*} \rho(00)=\text{empty word},\quad \rho(01)=1,\quad \rho(10)=0,\quad \rho(11)=01. \end{align*} $$
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 1
- Cited by



