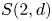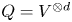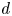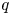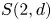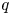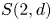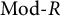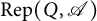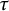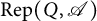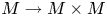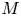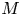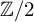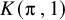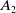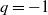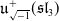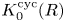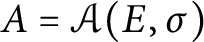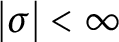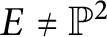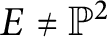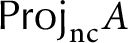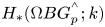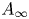121 results in 16Exx
Quasi-hereditary covers of Temperley–Lieb algebras and relative dominant dimension
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WHEN IS THE SILTING-DISCRETENESS INHERITED?
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-23
-
- Article
- Export citation
On tau-tilting subcategories
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 08 March 2024, pp. 1-38
-
- Article
- Export citation
Calabi–Yau structures on (quasi-)bisymplectic algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 26 September 2023, e87
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reflexive homology
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 August 2023, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Poincaré complex diagonals and the Bass trace conjecture
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 July 2023, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REAL TOPOLOGICAL HOCHSCHILD HOMOLOGY OF SCHEMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 07 June 2023, pp. 1461-1518
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable finiteness does not imply linear soficity
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 319-325
- Print publication:
- September 2023
-
- Article
- Export citation
Co-t-structures, cotilting and cotorsion pairs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 1 / July 2023
- Published online by Cambridge University Press:
- 10 March 2023, pp. 89-106
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Homological approximations in persistence theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 12 December 2022, pp. 66-103
- Print publication:
- February 2024
-
- Article
- Export citation
Riemann–Roch for stacky matrix factorizations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 06 December 2022, e108
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability conditions for contraction algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the computation of Hopf 2-cocycles with an example of diagonal type
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 24 June 2022, pp. 141-169
- Print publication:
- January 2023
-
- Article
- Export citation
Cluster categories of formal DG algebras and singularity categories
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 08 June 2022, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Witt vectors with coefficients and characteristic polynomials over non-commutative rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 26 April 2022, pp. 366-408
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Derived categories of skew-gentle algebras and orbifolds
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 31 January 2022, pp. 649-674
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HYPERSURFACE SUPPORT FOR NONCOMMUTATIVE COMPLETE INTERSECTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 731-750
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quantum projective planes finite over their centers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 10 January 2022, pp. 53-67
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cut cotorsion pairs
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 10 December 2021, pp. 548-585
- Print publication:
- September 2022
-
- Article
- Export citation
Massey products in the homology of the loop space of a p-completed classifying space: finite groups with cyclic Sylow p-subgroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 30 September 2021, pp. 908-915
-
- Article
-
- You have access
- Open access
- HTML
- Export citation