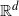52 results in 55Uxx
Adams’ cobar construction as a monoidal
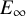 $E_{\infty }$-coalgebra model of the based loop space
$E_{\infty }$-coalgebra model of the based loop space
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 May 2024, e62
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extensions of the colorful Helly theorem for d-collapsible and d-Leray complexes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cohomology of a real toric variety and shellability of posets arising from a graph
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 03 November 2023, pp. 1044-1084
-
- Article
- Export citation
Categories of graphs for operadic structures
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 28 September 2023, pp. 155-212
- Print publication:
- January 2024
-
- Article
- Export citation
FIRST-ORDER HOMOTOPICAL LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 18 September 2023, pp. 1-63
-
- Article
- Export citation
Finite domination and Novikov homology over strongly $\mathbb {Z}^2$
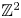 -graded rings
-graded rings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 July 2023, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cancellations of periodic orbits for non-singular Morse–Smale flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 25 May 2023, pp. 1123-1171
- Print publication:
- April 2024
-
- Article
- Export citation
Product decompositions of moment-angle manifolds and B-rigidity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1313-1325
- Print publication:
- December 2023
-
- Article
- Export citation
Approximate and discrete Euclidean vector bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 21 March 2023, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Morse theory of Bestvina–Brady type for posets and matchings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 09 February 2023, pp. 209-220
- Print publication:
- February 2024
-
- Article
- Export citation
Limit theory for U-statistics under geometric and topological constraints with rare events
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 14 September 2022, pp. 314-340
- Print publication:
- March 2023
-
- Article
- Export citation
Derived homotopy algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 25 July 2022, pp. 1198-1243
- Print publication:
- August 2023
-
- Article
- Export citation
The effective model structure and
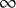 $\infty $
-groupoid objects
$\infty $
-groupoid objects
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CELLULAR CATEGORIES AND STABLE INDEPENDENCE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 18 May 2022, pp. 811-834
- Print publication:
- June 2023
-
- Article
- Export citation
On the homotopy and strong homotopy type of complexes of discrete Morse functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 February 2022, pp. 19-37
- Print publication:
- March 2023
-
- Article
- Export citation
CLASSIFYING SPACES AND THE LASCAR GROUP
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 13 September 2021, pp. 1396-1431
- Print publication:
- December 2021
-
- Article
- Export citation
UNITARY FUNCTOR CALCULUS WITH REALITY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 10 March 2021, pp. 197-230
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
Functional limit theorems for the euler characteristic process in the critical regime
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 17 March 2021, pp. 57-80
- Print publication:
- March 2021
-
- Article
- Export citation
Dwyer–Kan homotopy theory for cyclic operads
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 14 January 2021, pp. 29-58
-
- Article
- Export citation
HOMOTOPY MODEL THEORY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1301-1323
- Print publication:
- December 2021
-
- Article
- Export citation



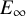
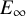
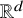
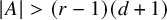

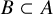
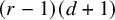
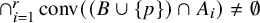
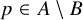
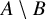
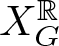
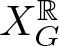
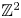

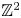
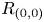
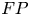
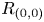
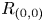
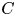
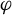
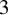
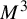
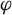
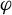
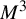
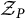
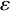
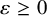
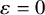
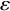
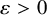
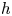
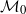
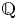
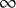
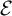
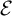
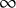
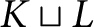

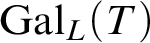
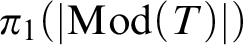
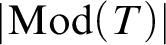
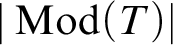
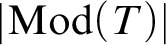
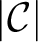
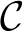
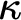
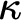
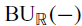 . The calculus produces a Taylor tower, the
. The calculus produces a Taylor tower, the 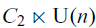 . We further give model categorical considerations, producing a zigzag of Quillen equivalences between spectra with an action of
. We further give model categorical considerations, producing a zigzag of Quillen equivalences between spectra with an action of