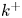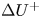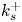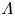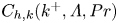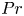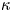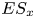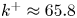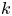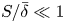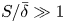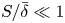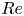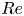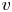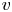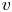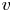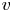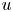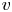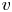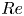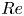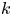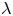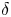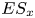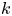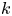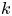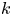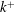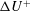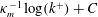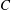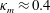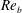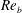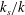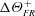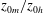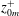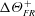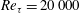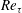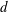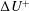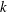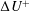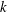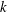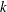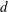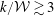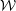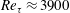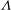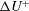39 results
Modelling the effect of roughness density on turbulent forced convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 979 / 25 January 2024
- Published online by Cambridge University Press:
- 11 January 2024, A22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A viscous vortex model for predicting the drag reduction of riblet surfaces
-
- Journal:
- Journal of Fluid Mechanics / Volume 978 / 10 January 2024
- Published online by Cambridge University Press:
- 05 January 2024, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reorganisation of turbulence by large and spanwise-varying riblets
-
- Journal:
- Journal of Fluid Mechanics / Volume 952 / 10 December 2022
- Published online by Cambridge University Press:
- 28 November 2022, A27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Impact of spanwise effective slope upon rough-wall turbulent channel flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 951 / 25 November 2022
- Published online by Cambridge University Press:
- 28 October 2022, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Investigation of unsteady secondary flows and large-scale turbulence in heterogeneous turbulent boundary layers
-
- Journal:
- Journal of Fluid Mechanics / Volume 934 / 10 March 2022
- Published online by Cambridge University Press:
- 19 January 2022, A40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mediterranean diet scoring systems: understanding the evolution and applications for Mediterranean and non-Mediterranean countries
-
- Journal:
- British Journal of Nutrition / Volume 128 / Issue 7 / 14 October 2022
- Published online by Cambridge University Press:
- 22 July 2021, pp. 1371-1392
- Print publication:
- 14 October 2022
-
- Article
-
- You have access
- HTML
- Export citation
Influence of riblet shapes on the occurrence of Kelvin–Helmholtz rollers
-
- Journal:
- Journal of Fluid Mechanics / Volume 913 / 25 April 2021
- Published online by Cambridge University Press:
- 02 March 2021, A37
-
- Article
- Export citation
Spanwise velocity statistics in high-Reynolds-number turbulent boundary layers
-
- Journal:
- Journal of Fluid Mechanics / Volume 913 / 25 April 2021
- Published online by Cambridge University Press:
- 02 March 2021, A35
-
- Article
- Export citation
Non-
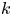 $k$-type behaviour of roughness when in-plane wavelength approaches the boundary layer thickness
$k$-type behaviour of roughness when in-plane wavelength approaches the boundary layer thickness
-
- Journal:
- Journal of Fluid Mechanics / Volume 911 / 25 March 2021
- Published online by Cambridge University Press:
- 22 January 2021, A1
-
- Article
- Export citation
Simultaneous skin friction and velocity measurements in high Reynolds number pipe and boundary layer flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 871 / 25 July 2019
- Published online by Cambridge University Press:
- 21 May 2019, pp. 377-400
-
- Article
- Export citation
Roughness effects in turbulent forced convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 861 / 25 February 2019
- Published online by Cambridge University Press:
- 19 December 2018, pp. 138-162
-
- Article
- Export citation
Secondary motion in turbulent pipe flow with three-dimensional roughness
-
- Journal:
- Journal of Fluid Mechanics / Volume 854 / 10 November 2018
- Published online by Cambridge University Press:
- 31 August 2018, pp. 5-33
-
- Article
- Export citation
Fully resolved measurements of turbulent boundary layer flows up to
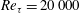 $Re_{\unicode[STIX]{x1D70F}}=20\,000$
$Re_{\unicode[STIX]{x1D70F}}=20\,000$
-
- Journal:
- Journal of Fluid Mechanics / Volume 851 / 25 September 2018
- Published online by Cambridge University Press:
- 20 July 2018, pp. 391-415
-
- Article
- Export citation
Similarity and structure of wall turbulence with lateral wall shear stress variations
-
- Journal:
- Journal of Fluid Mechanics / Volume 847 / 25 July 2018
- Published online by Cambridge University Press:
- 23 May 2018, pp. 591-613
-
- Article
- Export citation
Direct numerical simulation of high aspect ratio spanwise-aligned bars
-
- Journal:
- Journal of Fluid Mechanics / Volume 843 / 25 May 2018
- Published online by Cambridge University Press:
- 19 March 2018, pp. 126-155
-
- Article
- Export citation
The minimal-span channel for rough-wall turbulent flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 816 / 10 April 2017
- Published online by Cambridge University Press:
- 28 February 2017, pp. 5-42
-
- Article
- Export citation
Cross-stream stereoscopic particle image velocimetry of a modified turbulent boundary layer over directional surface pattern
-
- Journal:
- Journal of Fluid Mechanics / Volume 813 / 25 February 2017
- Published online by Cambridge University Press:
- 23 January 2017, pp. 412-435
-
- Article
- Export citation
Applicability of Taylor’s hypothesis in rough- and smooth-wall boundary layers
-
- Journal:
- Journal of Fluid Mechanics / Volume 812 / 10 February 2017
- Published online by Cambridge University Press:
- 28 December 2016, pp. 398-417
-
- Article
- Export citation
Turbulent flow over transitionally rough surfaces with varying roughness densities
-
- Journal:
- Journal of Fluid Mechanics / Volume 804 / 10 October 2016
- Published online by Cambridge University Press:
- 08 September 2016, pp. 130-161
-
- Article
- Export citation
Comparison of turbulent boundary layers over smooth and rough surfaces up to high Reynolds numbers – ERRATUM
-
- Journal:
- Journal of Fluid Mechanics / Volume 797 / 25 June 2016
- Published online by Cambridge University Press:
- 25 May 2016, p. 917
-
- Article
-
- You have access
- HTML
- Export citation