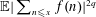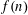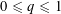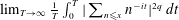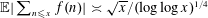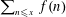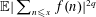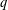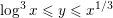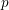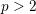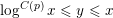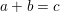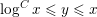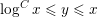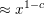22 results
Pop Music and Hip Ennui: A Sonic Fiction of Capitalist Realism. By Macon Holt. London: Bloomsbury Academic, 2019. 208 pp. ISBN 978-1-5013-4666-8
-
- Journal:
- Popular Music / Volume 39 / Issue 3-4 / December 2020
- Published online by Cambridge University Press:
- 19 March 2021, pp. 724-726
- Print publication:
- December 2020
-
- Article
- Export citation
MOMENTS OF RANDOM MULTIPLICATIVE FUNCTIONS, I: LOW MOMENTS, BETTER THAN SQUAREROOT CANCELLATION, AND CRITICAL MULTIPLICATIVE CHAOS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 January 2020, e1
-
- Article
-
- You have access
- Open access
- Export citation
An unexpected birth: neonatal resuscitation following a vaginal delivery by an unsuspecting mother in the emergency department: a case report
-
- Journal:
- Canadian Journal of Emergency Medicine / Volume 22 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 11 November 2019, pp. 254-256
- Print publication:
- March 2020
-
- Article
-
- You have access
- HTML
- Export citation
Personal Take: - Vaporwave is Dead, Long Live Vaporwave!
-
-
- Book:
- The Cambridge Companion to Music in Digital Culture
- Published online:
- 30 August 2019
- Print publication:
- 19 September 2019, pp 119-123
-
- Chapter
- Export citation
A new proof of Halász’s theorem, and its consequences
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 23 November 2018, pp. 126-163
- Print publication:
- January 2019
-
- Article
-
- You have access
- HTML
- Export citation
How Internet music is frying your brain1
-
- Journal:
- Popular Music / Volume 36 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 13 December 2016, pp. 86-97
- Print publication:
- January 2017
-
- Article
- Export citation
Anna Meredith, et al. - ‘VARMINTS’: ANNA MEREDITH . Anna Meredith (cl., keyboard, elecs), Sam Wilson (drums and perc.), Jack Ross (guit.) and Gemma Kost (vc). Moshi Moshi MOSHICD67 - ‘KATE SIMKO & LONDON ELECTRONIC ORCHESTRA’: KATE SIMKO . The Vinyl Factory VF204CD - ‘MINIATURISED CONCERTOS | MACHÉ’. Disc A (‘Miniaturised Concertos’): works by POPPY , PINNOCK , CASHIAN , RILEY ; Disc B (‘Maché’): works by MACLEOD , VINCENT , BELL , AKAMA , MURCOTT , CHADBURN , TUKHANEN , RICHARDS , ROWAN , PERKS , GLOVER , PAPAIOANNOU , VITKAUSKAITE , SUTHERLAND , MORGAN , MIYACHI , TIPP . Kate Halsall (pno and keyboards) with guests. Métier MSV 77205
-
- Article
- Export citation
Minor arcs, mean values, and restriction theory for exponential sums over smooth numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 23 February 2016, pp. 1121-1158
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
Contributors
-
-
- Book:
- The Cambridge Dictionary of Philosophy
- Published online:
- 05 August 2015
- Print publication:
- 27 April 2015, pp ix-xxx
-
- Chapter
- Export citation
Starspot variability and evolution from modeling Kepler photometry of active late-type stars
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 6 / Issue S273 / August 2010
- Published online by Cambridge University Press:
- 26 August 2011, pp. 78-82
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
Two new proofs of the Erdös–Kac Theorem, with bound on the rate of convergence, by Stein's method for distributional approximations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 147 / Issue 1 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 95-114
- Print publication:
- July 2009
-
- Article
- Export citation
Cardiovascular monitoring with acetylcholinesterase inhibitors: a clinical protocol
-
- Journal:
- Advances in Psychiatric Treatment / Volume 13 / Issue 3 / May 2007
- Published online by Cambridge University Press:
- 02 January 2018, pp. 178-184
- Print publication:
- May 2007
-
- Article
-
- You have access
- HTML
- Export citation
Contributors
-
-
- Book:
- The Cambridge Handbook of Age and Ageing
- Published online:
- 05 June 2016
- Print publication:
- 01 December 2005, pp xii-xvi
-
- Chapter
- Export citation
30. Commission des Vitesses Radiales Stellaires
-
- Journal:
- Transactions of the International Astronomical Union / Volume 6 / 1939
- Published online by Cambridge University Press:
- 25 April 2016, pp. 254-266
- Print publication:
- 1939
-
- Article
-
- You have access
- Export citation
24. Commission des Parallaxes Stellaires et des Mouvements Propres
-
- Journal:
- Transactions of the International Astronomical Union / Volume 6 / 1939
- Published online by Cambridge University Press:
- 25 April 2016, pp. 206-214
- Print publication:
- 1939
-
- Article
-
- You have access
- Export citation
24. Commission des Parallaxes Stellaires et des Mouvements Propres
-
- Journal:
- Transactions of the International Astronomical Union / Volume 5 / 1936
- Published online by Cambridge University Press:
- 25 April 2016, pp. 144-155
- Print publication:
- 1936
-
- Article
-
- You have access
- Export citation
30. Commission des Vitesses Radiales Stellaires
-
- Journal:
- Transactions of the International Astronomical Union / Volume 5 / 1936
- Published online by Cambridge University Press:
- 25 April 2016, pp. 188-196
- Print publication:
- 1936
-
- Article
-
- You have access
- Export citation