Research Article
Lifts of some tensor fields and connections to product preserving functors
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-41
-
- Article
-
- You have access
- Export citation
Tight closure in F-rational rings
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 43-54
-
- Article
-
- You have access
- Export citation
On vanishing of the twisted rational de Rham cohomology associated with hypergeometric functions
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 55-85
-
- Article
-
- You have access
- Export citation
Decomposition problem of probability measures related to monotone regularly varying functions
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 87-111
-
- Article
-
- You have access
- Export citation
The moments of the zeta-function on the line σ = 1
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 113-120
-
- Article
-
- You have access
- Export citation
Thick sets and quasisymmetric maps
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 121-148
-
- Article
-
- You have access
- Export citation
Other
Erratum to my paper: On the invariant differential metrics near pseudoconvex boundary points where the Levi form has corank one
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 149-152
-
- Article
-
- You have access
- Export citation
Research Article
Affine hypersurfaces with parallel cubic form
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 153-164
-
- Article
-
- You have access
- Export citation
Wiener-Hopf equation and Fredholm property of the Goursat problem in Gevrey space
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 165-196
-
- Article
-
- You have access
- Export citation
Des derivees de residus et une identite remarquable
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 197-206
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 135 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 135 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation



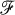 . We study algebraic properties of introduced lifts and we apply these lifts to prolongation of geometric structures from a manifold
. We study algebraic properties of introduced lifts and we apply these lifts to prolongation of geometric structures from a manifold 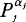 , integration being taken over some cycle. So we are led naturally to consider the twisted rational de Rham cohomology, which is a direct generalization of the usual de Rham cohomology to multivalued case.
, integration being taken over some cycle. So we are led naturally to consider the twisted rational de Rham cohomology, which is a direct generalization of the usual de Rham cohomology to multivalued case.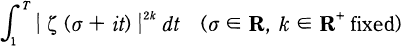
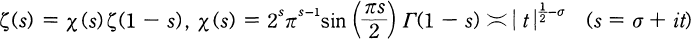
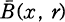 denote the closed ball with center
denote the closed ball with center 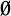 there is a
there is a 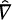 of the affine metric
of the affine metric 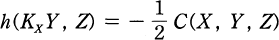 .
.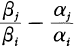 soient également non nulles pour
soient également non nulles pour 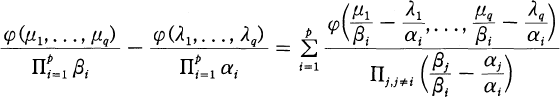 .
.