Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gutlyanskii, V. Ya.
and
Vuorinen, M.
1997.
On maps almost conformal at the boundary.
Complex Variables, Theory and Application: An International Journal,
Vol. 34,
Issue. 4,
p.
445.
Bishop, Christopher J.
and
Jones, Peter W.
1997.
Wiggly sets and limit sets.
Arkiv för Matematik,
Vol. 35,
Issue. 2,
p.
201.
Jonsson, Alf
and
Wallin, Hans
1997.
Boundary value problems and brownian motion on fractals.
Chaos, Solitons & Fractals,
Vol. 8,
Issue. 2,
p.
191.
Trotsenko, D. A.
1997.
Fractal straight lines and quasiconformal mappings.
Siberian Mathematical Journal,
Vol. 38,
Issue. 6,
p.
1206.
Alestalo, P.
Trotsenko, D. A.
and
Väisälä, J.
2001.
Isometric approximation.
Israel Journal of Mathematics,
Vol. 125,
Issue. 1,
p.
61.
Hästö, Peter
and
Ibragimov, Zair
2005.
Apollonian isometries of planar domains are Möbius mappings.
Journal of Geometric Analysis,
Vol. 15,
Issue. 2,
p.
229.
Prause, István
2007.
Flatness Properties of Quasispheres.
Computational Methods and Function Theory,
Vol. 7,
Issue. 2,
p.
527.
Anderson, G. D.
Qiu, S.-L.
and
Vuorinen, M.
2009.
Modular equations and distortion functions.
The Ramanujan Journal,
Vol. 18,
Issue. 2,
p.
147.
Huang, M.
Ponnusamy, S.
Wang, X.
and
Sahoo, S. K.
2010.
The Apollonian inner metric and uniform domains.
Mathematische Nachrichten,
Vol. 283,
Issue. 9,
p.
1277.
Trotsenko, D. A.
2011.
Gromov hyperbolic discrete spaces and their application to extension of classes of mappings.
Doklady Mathematics,
Vol. 83,
Issue. 3,
p.
344.
Trotsenko, D. A.
2011.
Uniform domains close to a ball.
Siberian Mathematical Journal,
Vol. 52,
Issue. 5,
p.
937.
Trotsenko, D. A.
2011.
Extendability of Classes of Maps and New Properties of Upper Sets.
Complex Analysis and Operator Theory,
Vol. 5,
Issue. 3,
p.
967.
Hariri, Parisa
Vuorinen, Matti
and
Zhang, Xiaohui
2017.
Inequalities and bi-Lipschitz conditions for the triangular ratio metric.
Rocky Mountain Journal of Mathematics,
Vol. 47,
Issue. 4,
Mahabadi, Sepideh
Makarychev, Konstantin
Makarychev, Yury
and
Razenshteyn, Ilya
2018.
Nonlinear dimension reduction via outer Bi-Lipschitz extensions.
p.
1088.
Hariri, Parisa
Klén, Riku
and
Vuorinen, Matti
2020.
Conformally Invariant Metrics and Quasiconformal Mappings.
p.
191.
Hariri, Parisa
Klén, Riku
and
Vuorinen, Matti
2020.
Conformally Invariant Metrics and Quasiconformal Mappings.
p.
209.
Afanas'eva, Olena
and
Bilet, Viktoriia
2021.
On a connection between some classes of mapping on Riemannian manifolds.
Proceedings of the Institute of Applied Mathematics and Mechanics NAS of Ukraine,
Vol. 34,
Issue. ,
p.
3.
Afanas’eva, Elena
2022.
Topological Properties of Regular Boundary Domains in Riemannian Manifolds.
Complex Analysis and Operator Theory,
Vol. 16,
Issue. 3,
Afanas’eva, Elena
and
Golberg, Anatoly
2022.
Topological mappings of finite area distortion.
Analysis and Mathematical Physics,
Vol. 12,
Issue. 2,
Afanas’eva, Elena
and
Golberg, Anatoly
2022.
Homeomorphisms of Finite Metric Distortion Between Riemannian Manifolds.
Computational Methods and Function Theory,
Vol. 22,
Issue. 4,
p.
755.
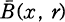 denote the closed ball with center x and radius r. We say that A is (q, k)-thick if for each x ∈ A and r> 0 such that A\
denote the closed ball with center x and radius r. We say that A is (q, k)-thick if for each x ∈ A and r> 0 such that A\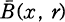 ≠
≠ 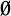 there is a k-simplex Δ with vertices in A ∩
there is a k-simplex Δ with vertices in A ∩ 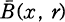 such that mk(Δ) ≥ qr.
such that mk(Δ) ≥ qr.



