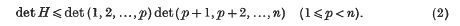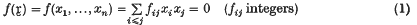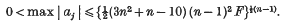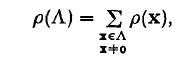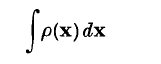Research Article
A note on commutators in free products. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 245-251
-
- Article
- Export citation
On semigroup algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-15
-
- Article
- Export citation
Sur les algèbres dérivées d'une algèbre de Lie
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 541-544
-
- Article
- Export citation
A non-nilpotent Lie ring satisfying the Engel condition and a non-nilpotent Engel group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 401-405
-
- Article
- Export citation
A note on valuations associated with a local domain
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 252-253
-
- Article
- Export citation
A generalized inverse for matrices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 406-413
-
- Article
-
- You have access
- Export citation
Remarks on the isomorphism problem in theories of construction of finite groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 16-24
-
- Article
- Export citation
A note on the AF + BΦ theorem and the theory of local rings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 545-550
-
- Article
- Export citation
Some inequalities concerning positive-definite Hermitian matrices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 414-421
-
- Article
- Export citation
Finite groups having unique proper characteristic subgroups. I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 25-36
-
- Article
- Export citation
Pairs of matrices with a non-zero commutator
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 551-553
-
- Article
- Export citation
On relations between certain intrinsic topologies in partially ordered sets
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 254-261
-
- Article
- Export citation
Bounds for the least solutions of homogeneous quadratic equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 262-264
-
- Article
- Export citation
Note on nilpotent and solvable algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 37-40
-
- Article
- Export citation
A class of transformations of the plane
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 554-564
-
- Article
- Export citation
The solution of linear differential equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 422-432
-
- Article
- Export citation
The α-dimensional measure of the graph and set of zeros of a Brownian path
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 265-274
-
- Article
- Export citation
A modified form of Siegel's mean-value theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 565-576
-
- Article
- Export citation
The solution of equations by iteration
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 41-43
-
- Article
- Export citation
The analysis of non-Markovian stochastic processes by the inclusion of supplementary variables
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 433-441
-
- Article
- Export citation




 , the concept of the group algebra (group ring) over
, the concept of the group algebra (group ring) over