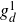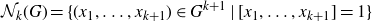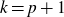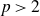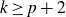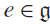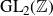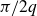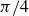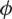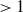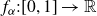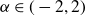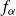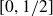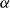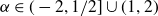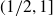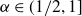Research Article
On the cohomology of Kobayashi’s plus/minus norm groups and applications
- Part of:
-
- Published online by Cambridge University Press:
- 11 May 2021, pp. 1-24
-
- Article
- Export citation
Chief factors in Polish groups
- Part of:
-
- Published online by Cambridge University Press:
- 30 June 2021, pp. 239-296
-
- Article
- Export citation
Tevelev degrees and Hurwitz moduli spaces
- Part of:
-
- Published online by Cambridge University Press:
- 03 December 2021, pp. 479-510
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Solving equations in dense Sidon sets
- Part of:
-
- Published online by Cambridge University Press:
- 19 May 2021, pp. 25-34
-
- Article
- Export citation
Trees of tangles in infinite separation systems
- Part of:
-
- Published online by Cambridge University Press:
- 22 July 2021, pp. 297-327
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-normality, topological transitivity and expanding families
- Part of:
-
- Published online by Cambridge University Press:
- 14 December 2021, pp. 511-523
-
- Article
- Export citation
Compact groups with a set of positive Haar measure satisfying a nilpotent law
- Part of:
-
- Published online by Cambridge University Press:
- 19 July 2021, pp. 329-332
-
- Article
- Export citation
Non-classical polynomials and the inverse theorem
-
- Published online by Cambridge University Press:
- 15 December 2021, pp. 525-537
-
- Article
- Export citation
Centers and Azumaya loci for finite W-algebras in positive characteristic
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2021, pp. 35-66
-
- Article
- Export citation
Counting and equidistribution in quaternionic Heisenberg groups
- Part of:
-
- Published online by Cambridge University Press:
- 08 July 2021, pp. 67-104
-
- Article
- Export citation
A positive proportion of locally soluble quartic Thue equations are globally insoluble
- Part of:
-
- Published online by Cambridge University Press:
- 05 August 2021, pp. 333-348
-
- Article
- Export citation
Asymptotics of sloshing eigenvalues for a triangular prism
- Part of:
-
- Published online by Cambridge University Press:
- 20 December 2021, pp. 539-571
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Permutable quasiregular maps
- Part of:
-
- Published online by Cambridge University Press:
- 03 June 2021, pp. 105-121
-
- Article
-
- You have access
- Open access
- Export citation
Algebraic cycles and intersections of three quadrics
- Part of:
-
- Published online by Cambridge University Press:
- 07 September 2021, pp. 349-367
-
- Article
- Export citation
Uniform perfectness of the Berkovich Julia sets in non-archimedean dynamics
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2021, pp. 573-590
-
- Article
- Export citation
Conformal geodesics on gravitational instantons
-
- Published online by Cambridge University Press:
- 09 July 2021, pp. 123-154
-
- Article
-
- You have access
- Open access
- Export citation
Step roots of Littlewood polynomials and the extrema of functions in the Takagi class
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2022, pp. 591-618
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Remarks about inhomogeneous pair correlations
- Part of:
-
- Published online by Cambridge University Press:
- 06 September 2021, pp. 369-386
-
- Article
- Export citation
Wild Galois representations: a family of hyperelliptic curves with large inertia image
- Part of:
-
- Published online by Cambridge University Press:
- 26 January 2022, pp. 619-633
-
- Article
- Export citation
Fourier duality in the Brascamp–Lieb inequality
- Part of:
-
- Published online by Cambridge University Press:
- 27 September 2021, pp. 387-409
-
- Article
- Export citation