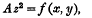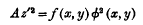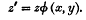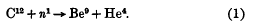Research Article
On the regularity of surfaces, II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 271-286
-
- Article
- Export citation
A theorem on Newton's polygon
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 287-296
-
- Article
- Export citation
Multiple canonical surfaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 297-308
-
- Article
- Export citation
On the ambiguity in the specification of a two-sheeted surface by its branch curve
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 309-314
-
- Article
- Export citation
Potential functions with periodicity in one coordinate
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 315-326
-
- Article
- Export citation
The vector representation of a sample
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 327-340
-
- Article
- Export citation
Foucault currents in cylindrical shells and ribbons
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 341-346
-
- Article
- Export citation
On the annihilation radiation of the positron
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 347-354
-
- Article
- Export citation
A hydrogen discharge tube for spectrographic work
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 355-356
-
- Article
- Export citation
Evidence for a new type of disintegration produced by neutrons
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 357-364
-
- Article
- Export citation
The flow due to a rotating disc
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 365-375
-
- Article
- Export citation
The heat of adsorption of hydrogen on tungsten
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 376-379
-
- Article
- Export citation
Front matter
PSP volume 30 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 30 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation



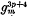 it is non-special and hence the redundancy of the base points is zero, therefore each of the double points of this system reduces the freedom by exactly three; and hence if we remove all the double points we get a system of curves of genus
it is non-special and hence the redundancy of the base points is zero, therefore each of the double points of this system reduces the freedom by exactly three; and hence if we remove all the double points we get a system of curves of genus