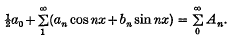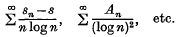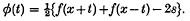Research Article
A note on some theorems on simultaneous diagonalization of two Hermitian matrices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 383-386
-
- Article
- Export citation
Manifolds of homotopy type K(π, 1). I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 387-393
-
- Article
- Export citation
The additive and multiplicative orders of a complex line-bundle
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 395-397
-
- Article
- Export citation
Embedding locally convex spaces in nearly exotic spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 399-400
-
- Article
- Export citation
Some forms of the closed graph theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 401-408
-
- Article
- Export citation
Small solutions of the congruence:
≡ 0 (mod p)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 409-412
-
- Article
- Export citation
The summation of Fourier series by logarithmic means
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 413-419
-
- Article
- Export citation
On the absolute summability and convergence of Fourier series and associated series
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 421-433
-
- Article
- Export citation
The uniform consistency of maximum-likelihood estimators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 435-439
-
- Article
- Export citation
Maximum-likelihood estimation in non-standard conditions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 441-450
-
- Article
- Export citation
On a singular integro-differential equation in aerofoil theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 451-454
-
- Article
- Export citation
Uniform progressing wave solutions of the wave equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 455-465
-
- Article
- Export citation
The response of an anisotropic elastic half-space to a rolling cylinder
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 467-484
-
- Article
- Export citation
A group theoretical approach to the many nucleon problem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 485-496
-
- Article
- Export citation
Other
Proceedings of the meetings held during the session 1970–71
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 497-501
-
- Article
- Export citation
Front matter
PSP volume 70 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 70 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b10
-
- Article
-
- You have access
- Export citation



 ; let
; let 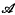 is a particular class of locally convex spaces then ℒ(
is a particular class of locally convex spaces then ℒ(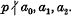 Mordell (4) has shown that for any sufficiently large prime p the congruence
Mordell (4) has shown that for any sufficiently large prime p the congruence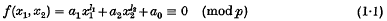


 and let
and let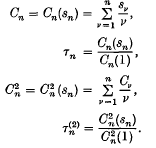
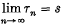 , we say that the series is summable (
, we say that the series is summable (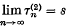 , the series is said to be summable (
, the series is said to be summable (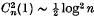 .
.