Research Article
Representing varieties of algebras by algebras
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-8
-
- Article
-
- You have access
- Export citation
A characterisation of the ellipsoid
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-394
-
- Article
-
- You have access
- Export citation
The iterated equation of generalized axially symmetric potential theory. V. Generalized weinstein correspondence principle
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-141
-
- Article
-
- You have access
- Export citation
Abelian p-subgroups of the general linear group
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-259
-
- Article
-
- You have access
- Export citation
Another characteristic conjugacy class of subgroups of finite soluble groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 395-400
-
- Article
-
- You have access
- Export citation
The H-function transform
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 142-148
-
- Article
-
- You have access
- Export citation
Second nilpotent BFC groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 9-18
-
- Article
-
- You have access
- Export citation
The Morse inequalities for line bundles
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 260-264
-
- Article
-
- You have access
- Export citation
An improved bound for BFCp-groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 19-27
-
- Article
-
- You have access
- Export citation
On groups with special antiautomorphisms
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 401-406
-
- Article
-
- You have access
- Export citation
The laminar free-convection boundary layer on a vertical heated plate in the neighbourhood of a discontinuity in plate temperature
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-168
-
- Article
-
- You have access
- Export citation
Composable topological properties and semigroups of relations
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 265-275
-
- Article
-
- You have access
- Export citation
Gibbs phenomenon for the Hausdorff means of double sequences1
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 169-185
-
- Article
-
- You have access
- Export citation
Generating groups for nilpotent varieties
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 28-32
-
- Article
-
- You have access
- Export citation
Radius of convexity of partial sums of a certain power series
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 407-410
-
- Article
-
- You have access
- Export citation
The second duals of certain spaces of analytic functions
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 276-280
-
- Article
-
- You have access
- Export citation
A note on centre-by-finite-exponent varieties of groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 33-36
-
- Article
-
- You have access
- Export citation
Positive linear operators and summability
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 281-290
-
- Article
-
- You have access
- Export citation
The uniqueness of bounded or measurable solutions of some functional equations
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 186-190
-
- Article
-
- You have access
- Export citation
The semigroup of endomorphisms of a Boolean ring
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 411-416
-
- Article
-
- You have access
- Export citation



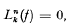
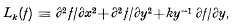
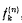 except that when
except that when 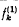 . It is easily shown [2, 3] that
. It is easily shown [2, 3] that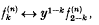
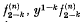 is a solution of (1).
is a solution of (1).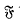 name be a class of finite soluble groups with the properties: (1)
name be a class of finite soluble groups with the properties: (1) 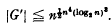
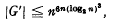
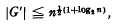
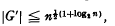
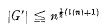
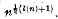 , and it is mv aim in this paper to take a first step towards closing the gap. This first, step is study of
, and it is mv aim in this paper to take a first step towards closing the gap. This first, step is study of 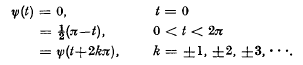
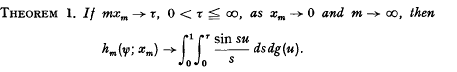
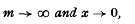
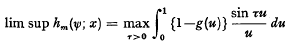
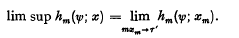
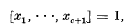
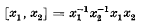 and, inductively,
and, inductively, 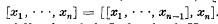 . Further, let
. Further, let 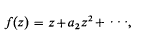
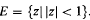 . G. Szegö [5] and Y. Miki [3] proved that if
. G. Szegö [5] and Y. Miki [3] proved that if 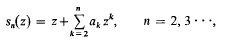
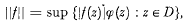
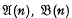 and
and 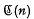 denote the varieties of groups defined by the laws (xy)
denote the varieties of groups defined by the laws (xy)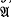
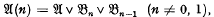 , thus clarifying the relationship between
, thus clarifying the relationship between 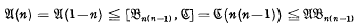
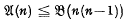
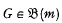 but
but 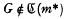 for any
for any 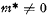 Thus
Thus 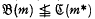 and
and 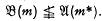 . It is also easy to see that in general
. It is also easy to see that in general 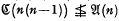 (see for instance [6] § 5.1) and we are led to ask
(see for instance [6] § 5.1) and we are led to ask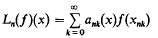
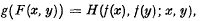
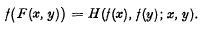
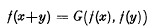
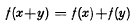
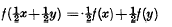
 (
(