Research Article
Effective bounds of the solutions of certain Diophantine equations
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-135
-
- Article
-
- You have access
- Export citation
Decomposability of finite rings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 136-138
-
- Article
-
- You have access
- Export citation
On the existence of sulutions of the equation Lx ∞ Nx and a coincidence degree theory
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 139-173
-
- Article
-
- You have access
- Export citation
Free groups, symmetric and reduced products
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 174-178
-
- Article
-
- You have access
- Export citation
Characterizations of collectively precompact and semi-precompact opterators on topological vector spaces
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 179-188
-
- Article
-
- You have access
- Export citation
Universal functions in several complex variables
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 189-196
-
- Article
-
- You have access
- Export citation
Weak convergence on non-separable metric spaces
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 197-204
-
- Article
-
- You have access
- Export citation
Differentiability and local rotundity
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 205-213
-
- Article
-
- You have access
- Export citation
On semigroups and groups of local polynomial functions
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 214-218
-
- Article
-
- You have access
- Export citation
Zero-set ultrafilters and Gδ-closures in uniform spaces
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 219-228
-
- Article
-
- You have access
- Export citation
Covering a polygon with triangles: a Caratheodory-type theorem
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 229-234
-
- Article
-
- You have access
- Export citation
Unambiguous evaluations of bidecic Jacobi and Jacobsthal sums
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 235-240
-
- Article
-
- You have access
- Export citation
On two-bridged knot polynomials
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 241-249
-
- Article
-
- You have access
- Export citation
Finitely presented groups of Fibonacci type. part II
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 250-256
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 28 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 28 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation



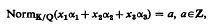
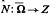 is a (possiblv nonlinear) mapping and Ω is a bounded open subset of
is a (possiblv nonlinear) mapping and Ω is a bounded open subset of 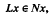
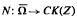 and
and