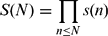Research Article
MORSE INEQUALITIES ON CERTAIN INFINITE 2-COMPLEXES
-
- Published online by Cambridge University Press:
- 09 August 2007, pp. 155-165
-
- Article
-
- You have access
- Export citation
ESTIMATES FOR MARCINKIEWICZ INTEGRALS IN BMO AND CAMPANATO SPACES
-
- Published online by Cambridge University Press:
- 09 August 2007, pp. 167-187
-
- Article
-
- You have access
- Export citation
ON AN OPEN QUESTION OF RICCERI CONCERNING A NEUMANN PROBLEM
-
- Published online by Cambridge University Press:
- 09 August 2007, pp. 189-195
-
- Article
-
- You have access
- Export citation
POSITIVE INCREASING SOLUTIONS ON THE HALF-LINE TO SECOND ORDER NONLINEAR DELAY DIFFERENTIAL EQUATIONS
-
- Published online by Cambridge University Press:
- 09 August 2007, pp. 197-211
-
- Article
-
- You have access
- Export citation
EXISTENCE OF A SOLUTION FOR A SINGULAR DIFFERENTIAL EQUATION WITH NONLINEAR FUNCTIONAL BOUNDARY CONDITIONS*
-
- Published online by Cambridge University Press:
- 09 August 2007, pp. 213-224
-
- Article
-
- You have access
- Export citation
PROPERTIES OF CERTAIN SUBALGEBRAS OF DALES-DAVIE ALGEBRAS
-
- Published online by Cambridge University Press:
- 09 August 2007, pp. 225-233
-
- Article
-
- You have access
- Export citation
RIGIDITY THEOREMS FOR HYPERSURFACES WITH CONSTANT SCALAR CURVATURE IN A UNIT SPHERE
-
- Published online by Cambridge University Press:
- 09 August 2007, pp. 235-241
-
- Article
-
- You have access
- Export citation
NOTE ON A PAPER OF J. HOFFSTEIN
-
- Published online by Cambridge University Press:
- 09 August 2007, pp. 243-255
-
- Article
-
- You have access
- Export citation
LINEAR FRACTIONAL RELATIONS IN BANACH SPACES: INTERIOR POINTS IN THE DOMAIN AND ANALOGUES OF THE LIOUVILLE THEOREM
-
- Published online by Cambridge University Press:
- 09 August 2007, pp. 257-268
-
- Article
-
- You have access
- Export citation
p-ADIC ORDER BOUNDED GROUP VALUATIONS ON ABELIAN GROUPS
-
- Published online by Cambridge University Press:
- 09 August 2007, pp. 269-279
-
- Article
-
- You have access
- Export citation
BANACH SPACES WITH SEPARABLE DUALS SUPPORT DUAL HYPERCYCLIC OPERATORS
-
- Published online by Cambridge University Press:
- 09 August 2007, pp. 281-290
-
- Article
-
- You have access
- Export citation
AN INTERTWINING OPERATOR FOR THE GROUP B2
-
- Published online by Cambridge University Press:
- 09 August 2007, pp. 291-319
-
- Article
-
- You have access
- Export citation
STABILITY OF MAPPINGS ON MULTI-NORMED SPACES
-
- Published online by Cambridge University Press:
- 09 August 2007, pp. 321-332
-
- Article
-
- You have access
- Export citation
ON THE FAMILY OF DIOPHANTINE TRIPLES {k − 1, k + 1, 16k3 − 4k}
-
- Published online by Cambridge University Press:
- 09 August 2007, pp. 333-344
-
- Article
-
- You have access
- Export citation
HARDY–BLOCH TYPE SPACES AND LACUNARY SERIES ON THE POLYDISK
-
- Published online by Cambridge University Press:
- 09 August 2007, pp. 345-356
-
- Article
-
- You have access
- Export citation
ON THE GEOMETRY OF THE SPACE OF ORIENTED LINES OF THE HYPERBOLIC SPACE
-
- Published online by Cambridge University Press:
- 09 August 2007, pp. 357-366
-
- Article
-
- You have access
- Export citation
A NOTE ON SIMULTANEOUS AND MULTIPLICATIVE DIOPHANTINE APPROXIMATION ON PLANAR CURVES
-
- Published online by Cambridge University Press:
- 09 August 2007, pp. 367-375
-
- Article
-
- You have access
- Export citation
POSITIVE SOLUTIONS FOR ASYMPTOTICALLY LINEAR ELLIPTIC SYSTEMS
-
- Published online by Cambridge University Press:
- 09 August 2007, pp. 377-390
-
- Article
-
- You have access
- Export citation
ON THE SQUARE-FREE PARTS OF ⌊en!⌋
-
- Published online by Cambridge University Press:
- 09 August 2007, pp. 391-403
-
- Article
-
- You have access
- Export citation
SAMELSON PRODUCTS OF SO(3) AND APPLICATIONS†
-
- Published online by Cambridge University Press:
- 09 August 2007, pp. 405-409
-
- Article
-
- You have access
- Export citation




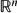 ) and Campanato spaces for the higher-dimensional Marcinkiewicz integral operator which is defined by
) and Campanato spaces for the higher-dimensional Marcinkiewicz integral operator which is defined by

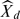 , the polynomial convex hull of
, the polynomial convex hull of 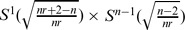 and
and 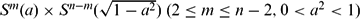 in a unit sphere
in a unit sphere 
 . Let
. Let 
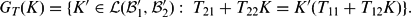
 with ramification index
with ramification index  , associated with the reflection group
, associated with the reflection group 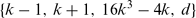
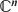 . Then we apply them to obtain sharp estimates for the mean growth in weighted spaces
. Then we apply them to obtain sharp estimates for the mean growth in weighted spaces 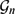 of oriented geodesics of
of oriented geodesics of 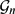 and
and 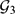 is Kähler and find an orthogonal almost complex structure on
is Kähler and find an orthogonal almost complex structure on 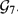 .
.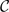 be a non-degenerate planar curve. We show that the curve is of Khintchine-type for convergence in the case of simultaneous approximation in
be a non-degenerate planar curve. We show that the curve is of Khintchine-type for convergence in the case of simultaneous approximation in 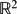 with two independent approximation functions; that is if a certain sum converges then the set of all points (
with two independent approximation functions; that is if a certain sum converges then the set of all points (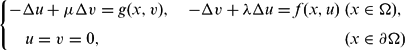
 ,
,  and asymptotically linear at infinity.
and asymptotically linear at infinity.