Research Article
On the Wielandt subgroup of infinite soluble groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 121-125
-
- Article
-
- You have access
- Export citation
Some subgroups of SL(3, z) generated by involutions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 127-136
-
- Article
-
- You have access
- Export citation
The modularity of the lattice of varieties of completely regular semigroups and related representations
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 137-152
-
- Article
-
- You have access
- Export citation
Uncountable existentially closed groups in locally finite group classes
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 153-163
-
- Article
-
- You have access
- Export citation
On permutation polynomials whose difference is linear
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 165-171
-
- Article
-
- You have access
- Export citation
Generalized fractions and Hughes' gradetheoretic analogue of the Cousin complex
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 173-188
-
- Article
-
- You have access
- Export citation
Inverse semigroups with certain types of partial automorphism monoids
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 189-195
-
- Article
-
- You have access
- Export citation
Graphs with near v- and e-neighbourhoods
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 197-199
-
- Article
-
- You have access
- Export citation
On Schachermayer's example about the Banach-Saks property
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 201-203
-
- Article
-
- You have access
- Export citation
Proximity and similarity of operators II
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 205-213
-
- Article
-
- You have access
- Export citation
Duals of Banach spaces of entire functions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 215-220
-
- Article
-
- You have access
- Export citation
On right duo p.p. rings
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 221-225
-
- Article
-
- You have access
- Export citation
Matrix invariants and complete intersections
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 227-229
-
- Article
-
- You have access
- Export citation
Subnormality and generalized commutation relations of families of operators†
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 231-238
-
- Article
-
- You have access
- Export citation
Conjugacy of free finite group actions on infranilmanifolds
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 239-240
-
- Article
-
- You have access
- Export citation
Union results for thin sets
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 241-254
-
- Article
-
- You have access
- Export citation
Homological stability for On,n over semi-local rings
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 255-259
-
- Article
-
- You have access
- Export citation
Corrigendum
Corrigendum
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 261-263
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 32 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 32 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation



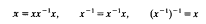
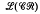 of subvarieties of the variety
of subvarieties of the variety 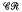 of completely regular semigroups, various results have been obtained which decompose special intervals in
of completely regular semigroups, various results have been obtained which decompose special intervals in 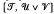 , where
, where 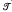 is the trivial variety and
is the trivial variety and 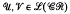 are subdirect products of
are subdirect products of 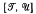 and
and 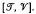 Pastijn and Trotter [13] show that certain intervals of the form
Pastijn and Trotter [13] show that certain intervals of the form 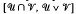 are direct products of the intervals
are direct products of the intervals 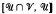 and
and 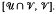 The main objective of this paper is to develop an appropriate lattice theoretic framework for these representations.
The main objective of this paper is to develop an appropriate lattice theoretic framework for these representations.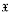 will always denote a local class of locally finite groups, which is closed with respect to subgroups, homomorphic images, extensions, and with respect to cartesian powers of finite
will always denote a local class of locally finite groups, which is closed with respect to subgroups, homomorphic images, extensions, and with respect to cartesian powers of finite  ) of all locally soluble π-groups (where π is a fixed set of primes). In [4], a wreath product construction was used in the study of existentially closed
) of all locally soluble π-groups (where π is a fixed set of primes). In [4], a wreath product construction was used in the study of existentially closed 
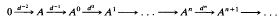
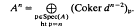
 (
(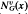 induced by the set of all vertices adjacent to
induced by the set of all vertices adjacent to 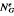 (
(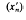 ) of (
) of (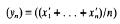
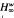 , respectively
, respectively 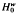 denote the Banach spaces of those entire functions φ(
denote the Banach spaces of those entire functions φ(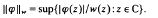
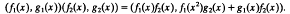
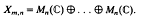
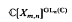
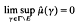 implies
implies 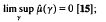
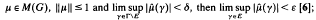 and
and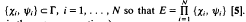 . (The multiplication indicated here is the group operation.)
. (The multiplication indicated here is the group operation.)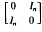 . The main result of this paper is the following theorem.
. The main result of this paper is the following theorem.