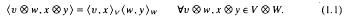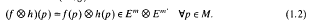Research Article
Polycyclic group rings and unique factorisation rings
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 135-144
-
- Article
-
- You have access
- Export citation
Extension of completely bounded A-B bimodule maps†
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 145-155
-
- Article
-
- You have access
- Export citation
Remarks on the range of a vector measure
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 157-161
-
- Article
-
- You have access
- Export citation
Associate subgroups of orthodox semigroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 163-171
-
- Article
-
- You have access
- Export citation
Symmetries of surfaces: an extension of Kulkarni's theorem
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 173-184
-
- Article
-
- You have access
- Export citation
Fitting classes of certain metanilpotent groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 185-195
-
- Article
-
- You have access
- Export citation
On reducible braids and composite braids
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 197-199
-
- Article
-
- You have access
- Export citation
Linearization of holomorphic mappings on fully nuclear spaces with a basis
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 201-208
-
- Article
-
- You have access
- Export citation
The structure of discontinuous homomorphisms from non-commutative C*-algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 209-218
-
- Article
-
- You have access
- Export citation
The kernel and trace operators for ideal extensions of regular semigroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 219-231
-
- Article
-
- You have access
- Export citation
Finite metacyclic groups acting on bordered surfaces
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 233-240
-
- Article
-
- You have access
- Export citation
On 𝓕-subnormal subgroups and Frattini-like subgroups of a finite group
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 241-247
-
- Article
-
- You have access
- Export citation
A weaker condition for normality
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 249-253
-
- Article
-
- You have access
- Export citation
Classification of tensor product immersions which are of 1-type
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 255-264
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 36 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 36 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

 (
(
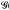 (
(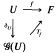
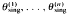 :
: 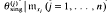
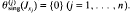 is a homomorphism, and
is a homomorphism, and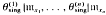
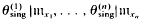 to map into rad(
to map into rad(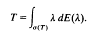
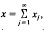 then this sum must converge unconditionally.
then this sum must converge unconditionally.