Hostname: page-component-5c6d5d7d68-wp2c8 Total loading time: 0 Render date: 2024-08-07T04:54:52.502Z Has data issue: false hasContentIssue false
  • English
  • Français

The structure of discontinuous homomorphisms from non-commutative C*-algebras

Published online by Cambridge University Press:  18 May 2009

Volker Runde
Volker Runde
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720, U.S.A.Vrunde@math. berkeley. edu
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a compact Hausdorff space, let C(X) denote the algebra of all continuous functions on X, let B be a Banach algebra, and let θ: → C(X) → B be a (possibly discontinuous) homomorphism with dense range. A classical theorem by W. G. Bade and P. C. Curtis ([2, Theorem 4.3]) describes in great detail the structure of θ we shall refer to this result as the Bade–Curtis theorem. Before we give a brief sketch of this theorem, we fix some notation. For Y ⊂ X let I(Y) and J(Y) denote the ideals of all functions in C(X) that vanish on Y and on a neighborhood of Y respectively; if Y = {x} for some x ɛ X, we write mx and Jx for I(Y) and J(Y) respectively. According to the Bade–Curtis theorem there is a finite set {x1,…, xn) ⊂ X, the so-called singularity set of θ, such that θ | ({x1, …, xn}) is continuous. As a consequence, the restriction of θ to the dense subalgebra of C (X) consisting of all those functions which are constant near each Xj (j = 1,…, n) is continuous, and extends to a continuous homomorphism θcont: C(X)→ B. Let θsing: = θ – θcont. Then θsing | I({x1,…, xn}) is a homomorphism onto a dense subalgebra of rad (B). θcont, and θsing are called the continuous and the singular part of θ respectively. Moreover, there are linear maps 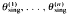: C(X)⊒ B such that

(i)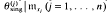

(ii) 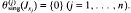is a homomorphism, and

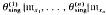
Condition (iii) forces the homomorphisms 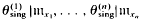to map into rad(B); such homomorphisms are called radical homomorphisms.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 36 , Issue 2 , May 1994 , pp. 209 - 218
Copyright
Copyright © Glasgow Mathematical Journal Trust 1994

References

REFERENCES

1.Albrecht, E. and Dales, H. G., Continuity of homomorphisms from C*-algebras and other Banach algebras, in Bachar, J. M., Bade, W. G., Curtis, P. C. Jr, Dales, H. G., and Thomas, M. P., Editors, Radical Banach algebras and automatic continuity, Volume 975 of Lecture Notes in Mathematics, (Springer Verlag, 1983), 375–396.CrossRefGoogle Scholar
2.Bade, W. G. and Curtis, P. C. Jr, Homomorphisms of commutative Banach algebras, Amer. J. Math. 82 (1960), 589–608.CrossRefGoogle Scholar
3.Dales, H. G., A discontinuous homomorphism from C(X). Amer. J. Math. 101 (1979), 647–734.CrossRefGoogle Scholar
4.Dales, H. G., Banach algebras and automatic continuity (Oxford University Press, in preparation).CrossRefGoogle Scholar
5.Dixmier, J., C*-algebras, (North-Holland Publishing Company, 1977).Google Scholar
6.Esterle, J., Solution d'un problème d'Erdös, Gillman et Henriksen et application à l'étude des homomorphismes de C(K), Acta Math. Acad. Sci. Hungar. 30 (1977), 113–127.CrossRefGoogle Scholar
7.Esterle, J., Injection des semigroupes divisibles dans les algèbres de convolution et construction d'homomorphismes discontinus de C(K), Proc. London Math. Soc. (3) 36 (1978), 59–85.CrossRefGoogle Scholar
8.Esterle, J., Sur I'existence d'un homomorphisme discontinu de C(K), Proc. London Math. Soc. (3) 36 (1978), 46–58.CrossRefGoogle Scholar
9.Johnson, B. E., Continuity of homomorphisms of algebras of operators, II, J. London Math. Soc. (2) 1 (1969), 81–84.CrossRefGoogle Scholar
10.Johnson, B. E., Norming C(Ώ) and related algebras, Trans. Amer. Math. Soc. 220 (1974), 37–58.Google Scholar
11.Laursen, K. B., Central factorization in C*-algebras and continuity of homomorphisms, J. London Math. Soc. (2) 28 (1983), 123–130.CrossRefGoogle Scholar
12.Laursen, K. B., Central factorization in C*-algebras and its use in automatic continuity, in Greenleaf, F. and Gulick, D., editors, Banach algebras and several complex variables, Contemporary Mathematics, 32 (1984), 169–176.Google Scholar
13.Laursen, K. B. and Sinclair, A. M., Lifting matrix units in C*-algebras, II, Math. Scand. 37 (1975), 167–172.CrossRefGoogle Scholar
14.Lazar, A. J. and Taylor, D. C., Multipliers of Pedersen's ideal, Mem. Amer. Math. Soc. 169 (1976).Google Scholar
15.Pedersen, G. K., Measure theory for C*-algebras, Math. Scand. 19 (1966), 131–146.CrossRefGoogle Scholar
16.Pedersen, G. K.. Measure theory for C*-algebras, II, Math. Scand. 22 (1968), 63–74.CrossRefGoogle Scholar
17.Pedersen, G. K., C*-algebras and their automorphism groups (Academic Press, 1979).Google Scholar
18.Pedersen, G. K., The corona construction, in Conway, J. B. and Morrel, B. B., editors, Operator Theory: Proceedings of the 1988 GPOTS-Wabash Conference, Pitman Research Notes in Mathematics Series, 225 (1990), 49–92.Google Scholar
19.Rickart, C. E., General theory of Banach algebras (Van Nostrand, 1960).Google Scholar
20.Sinclair, A. M., Homomorphisms from C*-algebras, Proc. London Math. Soc. (3) 29 (1974), 435–452.CrossRefGoogle Scholar
21.Sinclair, A. M., Homomorphisms from C(R), J. London Math. Soc. (2) 11 (1975), 165–174.CrossRefGoogle Scholar
22.Sinclair, A. M., Automatic continuity of linear operators, London Mathematical Society Lecture Notes Series (Cambridge University Press, 1976).CrossRefGoogle Scholar
23.Sinclair, A. M., Corrigendum: Homomorphisms from C*-algebras, Proc. London Math. Soc. (3) 32 (1976), 322.CrossRefGoogle Scholar
24.Somerset, D. W. B., Discontinuous homomorphisms from C*-algebras, Math. Proc. Cambridge Philos. Soc. 110 (1991), 147–150.CrossRefGoogle Scholar
25.Wright, F. B., A reduction for algebras of finite type, Ann. of Math. 60 (1954), 560–570.CrossRefGoogle Scholar