Research Article
Epsilon-hypercyclic operators
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 1597-1606
-
- Article
- Export citation
Sufficient conditions under which a transitive system is chaotic
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 1277-1310
-
- Article
- Export citation
On the norm convergence of non-conventional ergodic averages
-
- Published online by Cambridge University Press:
- 23 June 2009, pp. 321-338
-
- Article
- Export citation
Convex dynamics with constant input
-
- Published online by Cambridge University Press:
- 30 September 2009, pp. 957-972
-
- Article
- Export citation
Alternative proofs of linear response for piecewise expanding unimodal maps
-
- Published online by Cambridge University Press:
- 12 March 2009, pp. 1-20
-
- Article
-
- You have access
- Export citation
On the eigenvalues of finite rank Bratteli–Vershik dynamical systems
-
- Published online by Cambridge University Press:
- 30 September 2009, pp. 639-664
-
- Article
- Export citation
Persistence of wandering intervals in self-similar affine interval exchange transformations
-
- Published online by Cambridge University Press:
- 23 June 2009, pp. 665-686
-
- Article
- Export citation
Cohomology of substitution tiling spaces
-
- Published online by Cambridge University Press:
- 04 November 2009, pp. 1607-1627
-
- Article
- Export citation
Cone exchange transformations and boundedness of orbits
-
- Published online by Cambridge University Press:
- 07 September 2009, pp. 1311-1330
-
- Article
- Export citation
A sectional-Anosov connecting lemma
-
- Published online by Cambridge University Press:
- 21 July 2009, pp. 339-359
-
- Article
- Export citation
A characterization of ω-limit sets in shift spaces
-
- Published online by Cambridge University Press:
- 26 February 2009, pp. 21-31
-
- Article
- Export citation
Invariant measures on stationary Bratteli diagrams
-
- Published online by Cambridge University Press:
- 17 July 2009, pp. 973-1007
-
- Article
- Export citation
Non-abelian free group actions: Markov processes, the Abramov–Rohlin formula and Yuzvinskii’s formula
-
- Published online by Cambridge University Press:
- 13 October 2009, pp. 1629-1663
-
- Article
- Export citation
On t-entropy and variational principle for the spectral radius of weighted shift operators
-
- Published online by Cambridge University Press:
- 24 November 2009, pp. 1331-1342
-
- Article
- Export citation
Existence and convergence properties of physical measures for certain dynamical systems with holes
-
- Published online by Cambridge University Press:
- 24 November 2009, pp. 687-728
-
- Article
- Export citation
Partitions with independent iterates in random dynamical systems
-
- Published online by Cambridge University Press:
- 30 September 2009, pp. 361-377
-
- Article
- Export citation
Spectral sequences in Conley’s theory
-
- Published online by Cambridge University Press:
- 13 October 2009, pp. 1009-1054
-
- Article
- Export citation
Topologically transitive skew-products of operators
-
- Published online by Cambridge University Press:
- 30 March 2009, pp. 33-49
-
- Article
- Export citation
Livšic theorems for non-commutative groups including diffeomorphism groups and results on the existence of conformal structures for Anosov systems
-
- Published online by Cambridge University Press:
- 17 July 2009, pp. 1055-1100
-
- Article
- Export citation
Quasisymmetric conjugacy between quadratic dynamics and iterated function systems
-
- Published online by Cambridge University Press:
- 24 November 2009, pp. 1665-1684
-
- Article
- Export citation



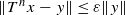 . The main result of this paper is a construction of a bounded linear operator
. The main result of this paper is a construction of a bounded linear operator 