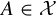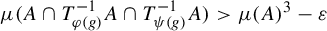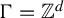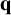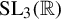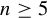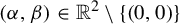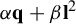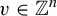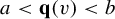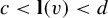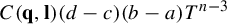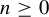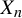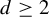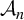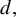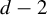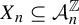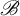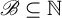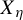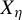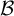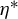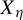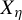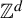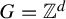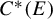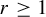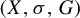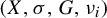FirstView articles
Original Article
Khintchine-type double recurrence in abelian groups
- Part of:
-
- Published online by Cambridge University Press:
- 24 April 2024, pp. 1-33
-
- Article
- Export citation
Schmidt games and Cantor winning sets
- Part of:
-
- Published online by Cambridge University Press:
- 19 April 2024, pp. 1-40
-
- Article
- Export citation
Asymptotic distribution for pairs of linear and quadratic forms at integral vectors
- Part of:
-
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-29
-
- Article
- Export citation
Similarities and differences between specification and non-uniform specification
- Part of:
-
- Published online by Cambridge University Press:
- 15 April 2024, pp. 1-29
-
- Article
- Export citation
Non-existence of a universal zero-entropy system via generic actions of almost complete growth
- Part of:
-
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1-15
-
- Article
- Export citation
On the Hausdorff dimension of invariant measures of piecewise smooth circle homeomorphisms
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Substreetutions and more on trees
- Part of:
-
- Published online by Cambridge University Press:
- 08 April 2024, pp. 1-55
-
- Article
- Export citation
Density of mode-locking property for quasi-periodically forced Arnold circle maps
- Part of:
-
- Published online by Cambridge University Press:
- 04 April 2024, pp. 1-36
-
- Article
- Export citation
Entropy, virtual Abelianness and Shannon orbit equivalence
- Part of:
-
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scale recurrence lemma and dimension formula for Cantor sets in the complex plane
- Part of:
-
- Published online by Cambridge University Press:
- 25 March 2024, pp. 1-42
-
- Article
- Export citation
Rigidity of pressures of Hölder potentials and the fitting of analytic functions through them
- Part of:
-
- Published online by Cambridge University Press:
- 18 March 2024, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Approximate homomorphisms and sofic approximations of orbit equivalence relations
- Part of:
-
- Published online by Cambridge University Press:
- 15 March 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Measure transfer and S-adic developments for subshifts
- Part of:
-
- Published online by Cambridge University Press:
- 11 March 2024, pp. 1-35
-
- Article
- Export citation
Invariant measures for
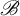 $\mathscr {B}$-free systems revisited
$\mathscr {B}$-free systems revisited
- Part of:
-
- Published online by Cambridge University Press:
- 08 March 2024, pp. 1-32
-
- Article
- Export citation
Bohr chaoticity of principal algebraic actions and Riesz product measures
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-integrability of the restricted three-body problem
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2024, pp. 1-29
-
- Article
- Export citation
An embedding theorem for subshifts over amenable groups with the comparison property
- Part of:
-
- Published online by Cambridge University Press:
- 05 March 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Patterson–Sullivan theory for groups with a strongly contracting element
- Part of:
-
- Published online by Cambridge University Press:
- 05 March 2024, pp. 1-56
-
- Article
- Export citation
Tracial weights on topological graph algebras
- Part of:
-
- Published online by Cambridge University Press:
- 05 March 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant measures of Toeplitz subshifts on non-amenable groups
- Part of:
-
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation