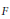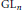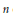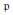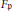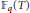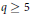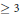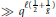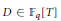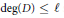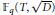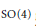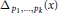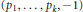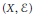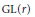Research Article
A Hypergraph with Commuting Partial Laplacians
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 385-397
-
- Article
-
- You have access
- Export citation
Exponents of Class Groups of Quadratic Function Fields over Finite Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 398-407
-
- Article
-
- You have access
- Export citation
Finite Groups Generated by Involutions on Lagrangian Planes of C2
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 408-419
-
- Article
-
- You have access
- Export citation
Approximation by Meromorphic Functions with Mittag-Leffler Type Constraints
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 420-428
-
- Article
-
- You have access
- Export citation
Ergodic Rotations of Nilmanifolds Conjugate to Their Inverses
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 429-439
-
- Article
-
- You have access
- Export citation
The Lehmer Polynomial and Pretzel Links
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 440-451
-
- Article
-
- You have access
- Export citation
Some Adjunction Properties of Ample Vector Bundles
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 452-458
-
- Article
-
- You have access
- Export citation
LS-catégorie algébrique et attachement de cellules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 459-468
-
- Article
-
- You have access
- Export citation
Sums and Products of Weighted Shifts
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 469-481
-
- Article
-
- You have access
- Export citation
Matching of Weighted Orbital Integrals for Metaplectic Correspondences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 482-490
-
- Article
-
- You have access
- Export citation
Resolution of Singularities of Null Cones
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 491-503
-
- Article
-
- You have access
- Export citation
Weak Amenability of a Class of Banach Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 504-508
-
- Article
-
- You have access
- Export citation
Other
Index of Volume 44
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 509-512
-
- Article
-
- You have access
- Export citation