Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zhang, Yong
2002.
Weak amenability of module extensions of Banach algebras.
Transactions of the American Mathematical Society,
Vol. 354,
Issue. 10,
p.
4131.
Gorgi, M. E.
and
Yazdanpanah, T.
2004.
Derivations into duals of ideals of Banach algebras.
Proceedings Mathematical Sciences,
Vol. 114,
Issue. 4,
p.
399.
Dashti, Mahshid
Nasr-Isfahani, Rasoul
and
Soltani Renani, Sima
2014.
Character Amenability of Lipschitz Algebras.
Canadian Mathematical Bulletin,
Vol. 57,
Issue. 1,
p.
37.
Abtahi, Fatemeh
Azizi,, Mohsen
and
Rejali, Ali
2017.
Character Amenability of the Intersection of Lipschitz Algebras.
Canadian Mathematical Bulletin,
Vol. 60,
Issue. 4,
p.
673.
Abtahi, F.
Byabani, E.
and
Rejali, A.
2019.
Some algebraic and homological properties of Lipschitz algebras and their second duals.
Archivum Mathematicum,
p.
211.
Khotanloo, A.
Esslamzadeh, G. H.
and
Tabatabaie Shourijeh, B.
2019.
A Unified Approach to Various Notions of Derivation.
Iranian Journal of Science and Technology, Transactions A: Science,
Vol. 43,
Issue. 5,
p.
2551.
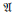 $\mathfrak{A}$ is a left ideal in its second dual algebra and has a left bounded approximate identity, then the weak amenability of
$\mathfrak{A}$ is a left ideal in its second dual algebra and has a left bounded approximate identity, then the weak amenability of 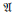 $\mathfrak{A}$ implies the
$\mathfrak{A}$ implies the 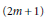 $\left( 2m+1 \right)$-weak amenability of
$\left( 2m+1 \right)$-weak amenability of 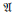 $\mathfrak{A}$ for all
$\mathfrak{A}$ for all 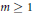 $m\,\ge \,1$.
$m\,\ge \,1$.

