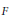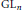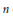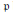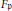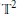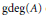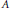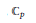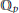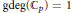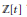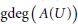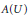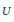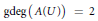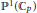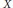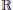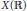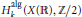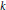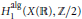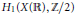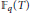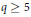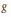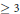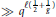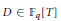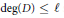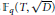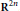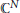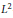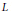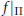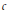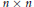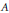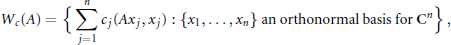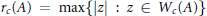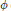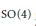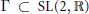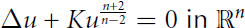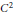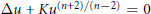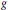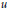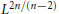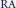Research Article
A Hypergraph with Commuting Partial Laplacians
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 385-397
-
- Article
-
- You have access
- Export citation
Linéarisation symplectique en dimension 2
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 129-139
-
- Article
-
- You have access
- Export citation
The Generating Degree of ℂp
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-11
-
- Article
-
- You have access
- Export citation
Algebraic Homology For Real Hyperelliptic and Real Projective Ruled Surfaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 257-265
-
- Article
-
- You have access
- Export citation
Extension of Maps to Nilpotent Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 266-269
-
- Article
-
- You have access
- Export citation
Exponents of Class Groups of Quadratic Function Fields over Finite Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 398-407
-
- Article
-
- You have access
- Export citation
On Quantizing Nilpotent and Solvable Basic Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 140-149
-
- Article
-
- You have access
- Export citation
A Technique of Studying Sums of Central Cantor Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 12-18
-
- Article
-
- You have access
- Export citation
Exceptional Sets of Slices for Functions From the Bergman Space in the Ball
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 150-159
-
- Article
-
- You have access
- Export citation
Linear Operators Preserving Generalized Numerical Ranges and Radii on Certain Triangular Algebras of Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 270-281
-
- Article
-
- You have access
- Export citation
Finite Groups Generated by Involutions on Lagrangian Planes of C2
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 408-419
-
- Article
-
- You have access
- Export citation
Multiplicities of Binary Recurrences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 19-21
-
- Article
-
- You have access
- Export citation
Approximation by Meromorphic Functions with Mittag-Leffler Type Constraints
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 420-428
-
- Article
-
- You have access
- Export citation
Hecke Operators on Jacobi-like Forms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 282-291
-
- Article
-
- You have access
- Export citation
The Trace Formula and Its Applications: An Introduction to the Work of James Arthur
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 160-209
-
- Article
-
- You have access
- Export citation
Gauss Sums of Orders Six and Twelve
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 22-26
-
- Article
-
- You have access
- Export citation
Ergodic Rotations of Nilmanifolds Conjugate to Their Inverses
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 429-439
-
- Article
-
- You have access
- Export citation
An Analogue of Napoleon’s Theorem in the Hyperbolic Plane
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 292-297
-
- Article
-
- You have access
- Export citation
Growth Estimates on Positive Solutions of the Equation
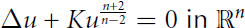
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 210-222
-
- Article
-
- You have access
- Export citation
Normal Subloops in the Integral Loop Ring of an RA Loop
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 27-35
-
- Article
-
- You have access
- Export citation