Article contents
Finite Groups Generated by Involutions on Lagrangian Planes of C2
Published online by Cambridge University Press: 20 November 2018
Abstract
We classify finite subgroups of 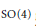 $\text{SO}\left( 4 \right)$ generated by anti-unitary involutions. They correspond to involutions fixing pointwise a Lagrangian plane. Explicit descriptions of the finite groups and the configurations of Lagrangian planes are obtained.
$\text{SO}\left( 4 \right)$ generated by anti-unitary involutions. They correspond to involutions fixing pointwise a Lagrangian plane. Explicit descriptions of the finite groups and the configurations of Lagrangian planes are obtained.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2001
References
- 3
- Cited by




