Hostname: page-component-7479d7b7d-wxhwt Total loading time: 0 Render date: 2024-07-13T16:16:25.759Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Adjunction Properties of Ample Vector Bundles

Published online by Cambridge University Press:  20 November 2018

Hironobu Ishihara
Hironobu Ishihara*
Affiliation:
Department of Mathematics Tokyo Institute of Technology Oh-okayama, Meguro Tokyo 152-8551 Japan, email: ishihara@math.titech.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 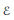$\mathcal{E}$ be an ample vector bundle of rank $r$ on a projective variety 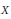$X$ with only log-terminal singularities. We consider the nefness of adjoint divisors 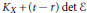${{K}_{X}}\,+\,\left( t-r \right)\,\det \,\mathcal{E}$ when 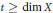$t\,\ge \,\dim\,X$ and 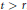$t\,>\,r$. As an application, we classify pairs 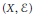$\left( X,\,\mathcal{E} \right)$ with ${{c}_{r}}$-sectional genus zero.

Keywords

14J6014C2014F0514J40ample vector bundleadjunctionsectional genus
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 44 , Issue 4 , 01 December 2001 , pp. 452 - 458
Copyright
Copyright © Canadian Mathematical Society 2001

References

[A] Andreatta, M., Some remarks on the study of good contractions. Manuscripta Math. 87 (1995), 359–367.Google Scholar
[AW] Andreatta, M. and Wísniewski, J. A., A note on nonvanishing and applications. Duke Math. J. 72 (1993), 739–755.Google Scholar
[Ba] Ballico, E., On vector bundles on 3-folds with sectional genus 1. Trans. Amer.Math. Soc. 324 (1991), 135–147.Google Scholar
[BS] Beltrametti, M. C. and Sommese, A. J., The Adjunction Theory of Complex Projective Varieties. In: Expositions in Math. 16, de Gruyter, 1995.Google Scholar
[F0] Fujita, T., Classification Theories of Polarized Varieties. LondonMath. Soc. Lecture Note Ser. 155, Cambridge University Press, 1990.Google Scholar
[F1] Fujita, T., On the structure of polarized varieties with Δ-genera zero. J. Fac. Sci. Univ. Tokyo 22 (1975), 103–115.Google Scholar
[F2] Fujita, T., Remarks on quasi-polarized varieties. Nagoya Math. J. 115 (1989), 105–123.Google Scholar
[FuI] Fukuma, Y. and Ishihara, H., A generalization of curve genus for ample vector bundles, II. Pacific J. Math. 193 (2000), 307–326.Google Scholar
[I] Ishihara, H., A generalization of curve genus for ample vector bundles, I. Comm. Algebra 27 (1999), 4327–4335.Google Scholar
[K] Kawamata, Y., On the length of an extremal rational curve. Invent.Math. 105 (1991), 609–611.Google Scholar
[LM] Lanteri, A. and Maeda, H., Ample vector bundles of curve genus one. Canad. Math. Bull. 42 (1999), 209–213.Google Scholar
[LMS] Lanteri, A., Maeda, H. and Sommese, A. J., Ample and spanned vector bundles of minimal curve genus. Arch. Math. (Basel) 66 (1996), 141–149.Google Scholar
[M1] Maeda, H., Ramification divisors for branched coverings of Pn . Math. Ann. 288 (1990), 195–199.Google Scholar
[M2] Maeda, H., Ample vector bundles of small curve genera. Arch. Math. (Basel) 70 (1998), 239–243.Google Scholar
[Me] Mella, M., Vector bundles on log terminal varieties. Proc. Amer.Math. Soc. 126 (1998), 2199–2204.Google Scholar
[YZ] Ye, Y. G. and Zhang, Q., On ample vector bundles whose adjunction bundles are not numerically effective. Duke Math. J. 60 (1990), 671–687.Google Scholar
[Z1] Zhang, Q., Ample vector bundles on singular varieties. Math. Z. 220 (1995), 59–64.Google Scholar
[Z2] Zhang, Q., Ample vector bundles on singular varieties II. Math. Ann. 307 (1997), 505–509.Google Scholar