Research Article
Corner Behavior of Solutions of Semilinear Dirichlet Problems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1025-1046
-
- Article
-
- You have access
- Export citation
Automorphisms of G-Azumaya Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1047-1058
-
- Article
-
- You have access
- Export citation
Characterizations for Prime Semilattices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1059-1073
-
- Article
-
- You have access
- Export citation
Generalized Gradients, Lipschitz behavior and Directional Derivatives
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1074-1084
-
- Article
-
- You have access
- Export citation
Approximation by Λ-Splines on the Circle
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1085-1111
-
- Article
-
- You have access
- Export citation
The Strong ϕ Topology on Symmetric Sequence Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1112-1133
-
- Article
-
- You have access
- Export citation
Centres of Rank-Metric Completions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1134-1148
-
- Article
-
- You have access
- Export citation
A Note on the Multiplicity of Cohen-Macaulay Algebras with Pure Resolutions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1149-1162
-
- Article
-
- You have access
- Export citation
Partitioning Projective Geometries into Caps
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1163-1175
-
- Article
-
- You have access
- Export citation
Estimates for Solutions of Wave Equations with Vanishing Curvature
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1176-1200
-
- Article
-
- You have access
- Export citation
Directed Graphs and the Jacobi-Trudi Identity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1201-1210
-
- Article
-
- You have access
- Export citation
Generalized Spectral Theory in Complex Banach Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1211-1236
-
- Article
-
- You have access
- Export citation
A measure on the Unipotent Variety
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1237-1274
-
- Article
-
- You have access
- Export citation



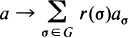
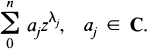
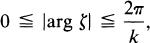
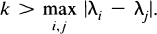
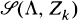 or
or 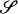 the class of Λ-splines
the class of Λ-splines 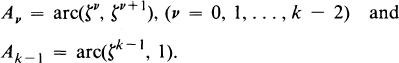
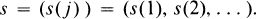
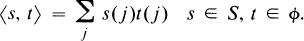
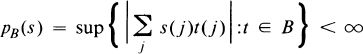
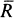 , is a right and left self-injective regular ring. Let
, is a right and left self-injective regular ring. Let 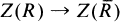 .
.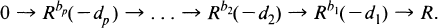
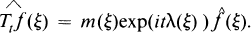
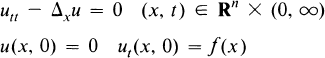
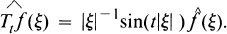
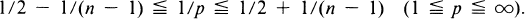
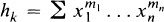
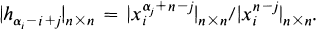
 with identit
with identit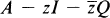 has no inverse in
has no inverse in 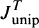 . We shall recall the precise definition in Section 1.
. We shall recall the precise definition in Section 1.