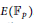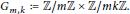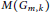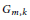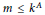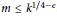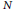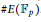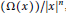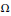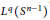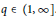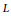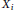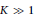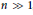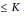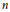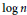Research Article
The Frequency of Elliptic Curve Groups over Prime Finite Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 721-761
-
- Article
-
- You have access
- Export citation
On a Linear Refinement of the Prékopa-Leindler Inequality
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 762-783
-
- Article
-
- You have access
- Export citation
Toric Degenerations and Laurent Polynomials Related to Givental's Landau–Ginzburg Models
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 784-815
-
- Article
-
- You have access
- Export citation
On the Commutators of Singular Integral Operators with Rough Convolution Kernels
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 816-840
-
- Article
-
- You have access
- Export citation
Characterizing the Absolute Continuity of the Convolution of Orbital Measures in a Classical Lie Algebra
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 841-875
-
- Article
-
- You have access
- Export citation
Metric Spaces Admitting Low-distortion Embeddings into All n-dimensional Banach Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 876-907
-
- Article
-
- You have access
- Export citation
Existence of Hilbert Cusp Forms with Non-vanishing L-values
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 908-960
-
- Article
-
- You have access
- Export citation