Letting 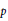$p$ vary over all primes and 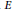$E$ vary over all elliptic curves over the finite field 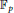${{\mathbb{F}}_{p}}$, we study the frequency to which a given group 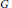$G$ arises as a group of points 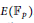$E\left( {{\mathbb{F}}_{p}} \right)$. It is well known that the only permissible groups are of the form 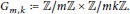${{G}_{m,\,k}}\,:=\,\mathbb{Z}\,/m\mathbb{Z}\,\times \,\mathbb{Z}/mk\mathbb{Z}$. Given such a candidate group, we let 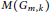$M\left( {{G}_{m,\,k}} \right)$ be the frequency to which the group 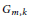${{G}_{m,\,k}}$ arises in this way. Previously, C.David and E. Smith determined an asymptotic formula for 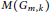$M\left( {{G}_{m,\,k}} \right)$ assuming a conjecture about primes in short arithmetic progressions. In this paper, we prove several unconditional bounds for 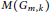$M\left( {{G}_{m,\,k}} \right)$, pointwise and on average. In particular, we show that 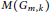$M\left( {{G}_{m,\,k}} \right)$ is bounded above by a constant multiple of the expected quantity when 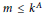$m\,\le \,{{k}^{A}}$ and that the conjectured asymptotic for 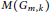$M\left( {{G}_{m,\,k}} \right)$ holds for almost all groups 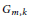${{G}_{m,\,k}}$ when 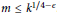$m\,\le \,{{k}^{1/4-\in }}$. We also apply our methods to study the frequency to which a given integer 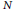$N$ arises as a group order $\#E\left( {{\mathbb{F}}_{p}} \right)$.