Article contents
Existence of Hilbert Cusp Forms with Non-vanishing L-values
Published online by Cambridge University Press: 20 November 2018
Abstract
We develop a derivative version of the relative trace formula on 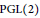 $\text{PGL}\left( 2 \right)$ studied in our previous work, and derive an asymptotic formula of an average of central values (derivatives) of automorphic
$\text{PGL}\left( 2 \right)$ studied in our previous work, and derive an asymptotic formula of an average of central values (derivatives) of automorphic 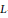 $L$-functions for Hilbert cusp forms. As an application, we prove the existence of Hilbert cusp forms with non-vanishing central values (derivatives) such that the absolute degrees of their Hecke fields are arbitrarily large.
$L$-functions for Hilbert cusp forms. As an application, we prove the existence of Hilbert cusp forms with non-vanishing central values (derivatives) such that the absolute degrees of their Hecke fields are arbitrarily large.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2016
References
- 3
- Cited by


