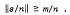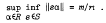Research Article
Coproducts of De Morgan algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-13
-
- Article
-
- You have access
- Export citation
Arithmetic properties of certain functions in several variables III
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 15-47
-
- Article
-
- You have access
- Export citation
On common fixed point theorems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 49-53
-
- Article
-
- You have access
- Export citation
A classification of groups with a centralizer condition II
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 55-60
-
- Article
-
- You have access
- Export citation
Pseudo-autonomous linear systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 61-65
-
- Article
-
- You have access
- Export citation
A formula for the exact number of primes below a given bound in any arithmetic progression
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 67-73
-
- Article
-
- You have access
- Export citation
A commutativity theorem for rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 75-77
-
- Article
-
- You have access
- Export citation
A counterexample to the density of the space generated by the composition operators
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 79-81
-
- Article
-
- You have access
- Export citation
Multiplicative relations in number fields
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 83-98
-
- Article
-
- You have access
- Export citation
Stability of impulsively perturbed systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 99-110
-
- Article
-
- You have access
- Export citation
On the optimal control of a manufacturing firm
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 111-123
-
- Article
-
- You have access
- Export citation
On a conjecture of Mahler
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 125-129
-
- Article
-
- You have access
- Export citation
Varieties of a closed category
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 131-145
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD theses
The isomorphism semigroup of a group
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 147-149
-
- Article
-
- You have access
- Export citation
A geometry with spinor connection as a model for space, time and matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 151-152
-
- Article
-
- You have access
- Export citation
Estimation for vector linear time series models
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 153-154
-
- Article
-
- You have access
- Export citation
Models of well-orderings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 155-157
-
- Article
-
- You have access
- Export citation
Topological measure theory, with applications to probability
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 159-160
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 16 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 16 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation