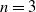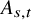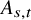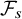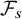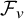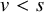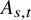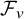1655 results in 60Jxx
The impact of pinning points on memorylessness in Lévy random bridges
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 15 October 2024, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
Stationary measures and the continuous-state branching process conditioned on extinction
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 07 October 2024, pp. 1-27
-
- Article
-
- You have access
- HTML
- Export citation
Boundary crossing problems and functional transformations for Ornstein–Uhlenbeck processes
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 07 October 2024, pp. 1-27
-
- Article
-
- You have access
- HTML
- Export citation
Maximum likelihood estimation for spinal-structured trees
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 03 October 2024, pp. 1-35
-
- Article
-
- You have access
- HTML
- Export citation
Transience of continuous-time conservative random walks
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-19
-
- Article
-
- You have access
- HTML
- Export citation
Efficiency of reversible MCMC methods: elementary derivations and applications to composite methods
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-21
-
- Article
-
- You have access
- HTML
- Export citation
Maximizing the probability of visiting a set infinitely often for a Markov decision process with Borel state and action spaces
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 22 August 2024, pp. 1-24
-
- Article
-
- You have access
- HTML
- Export citation
Optimal drift rate control and two-sided impulse control for a Brownian system with the long-run average criterion
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 31 July 2024, pp. 1-34
-
- Article
-
- You have access
- HTML
- Export citation
Error bounds for one-dimensional constrained Langevin approximations for nearly density-dependent Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 26 July 2024, pp. 825-867
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Convergence of hybrid slice sampling via spectral gap
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 25 July 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Persistence of spectral projections for stochastic operators on large tensor products
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maintenance of steady-state mRNA levels by a microRNA-based feed forward loop in the presence of stochastic gene expression noise
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 29 May 2024, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
(Almost) complete characterization of the stability of a discrete-time Hawkes process with inhibition and memory of length two
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1-22
-
- Article
-
- You have access
- HTML
- Export citation
Perturbation analysis for continuous-time Markov chains in a weak sense
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1-23
-
- Article
-
- You have access
- HTML
- Export citation
Branching processes in nearly degenerate varying environment
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1-20
-
- Article
-
- You have access
- HTML
- Export citation
Recurrence and transience of a Markov chain on
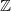 $\mathbb Z$+ and evaluation of prior distributions for a Poisson mean
$\mathbb Z$+ and evaluation of prior distributions for a Poisson mean
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 25 April 2024, pp. 1-19
-
- Article
-
- You have access
- HTML
- Export citation
Uniform propagation of chaos for a dollar exchange econophysics model
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 22 April 2024, pp. 1-13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Macroscopic limit of a Fokker-Planck model of swarming rigid bodies
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 19 April 2024, pp. 1-49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An extension of the stochastic sewing lemma and applications to fractional stochastic calculus
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 April 2024, e52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convergence of the height process of supercritical Galton–Watson forests with an application to the configuration model in the critical window
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1064-1105
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation