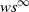1. Introduction
Markov decision processes (MDPs) are a family of controlled stochastic processes which are suitable for the modeling of several sequential decision-making problems under uncertainty. They arise in many applications, such as engineering, computer science, telecommunications, finance, etc. Their study started in the late 1950s and the early 1960s with the seminal works of Bellman, Blackwell, Howard, and Veinott, to name just a few authors; see, e.g., [Reference Bellman8, Reference Howard21]. Both the theoretical foundations and applications of MDPs continue to be areas of active research. From a theoretical point of view, there are several techniques which allow one to establish the existence of optimal controls, as well as to analyze the main features of the optimal value function. Roughly speaking, there exist two families of such techniques. The first is related to the dynamic programming principle established by Bellman, and is also known as the backward induction principle for the finite-horizon case. In this framework, the optimality equation states that the value function is the fixed point of an operator (the so-called Bellman operator) which incorporates the current cost plus an expected value related to future costs. This approach and its various extensions, such as the value iteration and policy iteration algorithms, are studied in detail in the references [Reference Bäuerle and Rieder6, Reference Bertsekas and Tsitsiklis9, Reference Dynkin and Yushkevich16, Reference Hernández-Lerma and Lasserre18–Reference Hinderer20, Reference Puterman26, Reference Sennott32] (this is a non-exhaustive list). The second family of methods is based on an equivalent formulation of MDPs in a linear programming context. The key idea is to transform the original dynamic control problem into an infinite-dimensional static optimization problem over a space of finite measures. In this setting, the underlying variables of the linear program are given by the occupation measures of the controlled process, satisfying the so-called characteristic equation, and the value of the linear program is the integral of the one-step cost function with respect to an occupation measure. This last technique is particularly well adapted to problems with constraints; see the references [Reference Borkar10, Reference Hernández-Lerma and Lasserre18, Reference Piunovskiy24–Reference Puterman26], among others, for a detailed presentation and analysis of this approach. Although different, these two approaches share a common characteristic: namely, they are well adapted to additive-type performance criteria, but they do not allow for the study of non-additive performance criteria.
It must be emphasized that the non-additive type of criterion has undergone significant development in recent years; see for example the risk-sensitive optimality criterion [Reference Bäuerle and Rieder7, Reference Cavazos-Cadena12, Reference Zhang34] and the so-called gambling houses [Reference Venel and Ziliotto33]. The distinctive feature of these non-additive criteria is that the criterion to be optimized cannot be decomposed as the sum of individual contributions (typically, the rewards earned at each single transition), nor is it linearly related to such sums (as for the classical long-run average-reward optimality criterion). Non-additive criteria introduce some nonlinearity in the objective function via, e.g., a utility function. For instance, in risk-sensitive models, the criterion to be maximized is the expected utility of the total rewards over a finite time horizon or the total discounted rewards over an infinite time horizon. Nonlinearity is introduced precisely by the utility function, which often takes the form of a power function or a logarithmic function. The usual technique for dealing with such problems is to develop an ad hoc dynamic-programming-like approach by introducing an operator which is nonlinear in the reward function. In gambling house problems, the expectation of a long-run average reward is maximized, making this again a nonlinear problem. Conditions under which this problem corresponds, in fact, to an average-reward MDP are studied. In summary, non-additive problems are usually tackled by relating them to other standard additive problems or by using operators resembling the Bellman principle. For the problem we are interested in, which is also of a non-additive nature, Schäl [Reference Schäl31] developed a ‘vanishing discount factor’ approach based on total-expected-reward MDPs (details are given in the next paragraph).
In this paper, we study another non-additive optimality criterion which aims at maximizing the probability of visiting a certain subset of the state space infinitely often. This criterion is also asymptotic; more precisely, the performance function cannot be approximated by finite-horizon criteria, since the distribution of the state process over a finite horizon does not allow one to characterize the whole history of the process (or at least its tails) and contains no relevant information about whether a subset of the state space has been reached infinitely often. It is important to emphasize that this optimality criterion has been very little studied in the literature. To the best of our knowledge, it was first studied by Schäl in [Reference Schäl31], who showed the existence of an optimal deterministic stationary policy in the context of an MDP with finite state space. More recently, in [Reference Dufour and Prieto-Rumeau15], this existence result has been generalized to models with countable state space. The approach proposed by Schäl in [Reference Schäl31] uses properties of continuity of matrix inversion and of fundamental matrices of finite-state Markov chains and is therefore restricted to the finite-state framework. The results obtained in [Reference Dufour and Prieto-Rumeau15] rely heavily on the fact that the state space is countable. It should be noted that in this particular context the space of deterministic stationary policies is compact with respect to pointwise convergence.
The objective of the present paper is to extend these results to a model with a general Borel state space and to show the existence of an optimal randomized stationary policy. This is a continuation of the results presented in [Reference Dufour and Prieto-Rumeau15], in the sense that we take up the idea of introducing an auxiliary control model as a means of analyzing the original control model. This auxiliary model is an MDP with total expected reward that, roughly speaking, can be studied by finding a suitable topology on the set of strategic probability measures to ensure that this set is compact and the expected reward functional is semicontinuous.
In relation to [Reference Dufour and Prieto-Rumeau15], an important difficulty in our paper is to show, in the context of a general state space, the compactness of the space of strategic measures induced by randomized stationary policies; this is unlike the case of a countable state space, for which the proof was straightforward. Our approach relies on the introduction of Young measures to model randomized stationary policies and thus endow this space with a topology. In this framework, the space of stationary strategic measures can be seen as the image of the space of Young measures under a certain map. The difficulty is to show the continuity of this map. Another delicate point is to provide a sufficient condition to ensure the continuity of the criterion for the auxiliary model that is written as a function on the space of strategic measures. In [Reference Dufour and Prieto-Rumeau15], a condition is formulated in terms of the entrance time to the set of recurrent states. This condition is based on the fact that the countable state space of a Markov chain can be split into two classes: recurrent and transient states. In the context of a general state space, this structural property is not that simple. To overcome this difficulty, we introduce a general condition imposing a drift condition by using standard Foster–Lyapunov criteria. Under these conditions, we are able to prove that the problem of maximizing the probability of visiting a set infinitely often has an optimal policy which is Markov stationary. It is worth stressing that the result on the compactness of strategic probability measures for stationary Markov policies (Theorem 2.1) is a new result and is interesting in itself, not just in the context of the specific control model in this paper.
The problem studied in this paper (that of maximizing the probability of visiting a subset of the state space infinitely often) can be applied in population dynamics problems in which the population is controlled so as to be driven to some target set or to avoid some set. Indeed, the symmetric problem of minimizing the probability of being absorbed by some subset of the state space can be interpreted as the problem of preventing the population from being trapped in some region of the state space. Research is currently in progress on a game-theoretic approach to this problem, in which two competing species try to drive each other out of some region of the state space by maximizing or minimizing the probabilities of remaining in that region from some time onward.
Notation. We now introduce some notation used throughout the paper. We will write
![]() $\mathbb{N}=\{0,1,2,\ldots\}$
. On a measurable space
$\mathbb{N}=\{0,1,2,\ldots\}$
. On a measurable space
![]() $(\boldsymbol{\Omega},\boldsymbol{\mathcal{F}})$
we will write
$(\boldsymbol{\Omega},\boldsymbol{\mathcal{F}})$
we will write
![]() $\boldsymbol{\mathcal{P}}(\boldsymbol{\Omega})$
for the set of probability measures, assuming that there is no risk of confusion regarding the
$\boldsymbol{\mathcal{P}}(\boldsymbol{\Omega})$
for the set of probability measures, assuming that there is no risk of confusion regarding the
![]() $\sigma$
-algebra on
$\sigma$
-algebra on
![]() $\boldsymbol{\Omega}$
. If
$\boldsymbol{\Omega}$
. If
![]() $(\boldsymbol{\Omega'},\boldsymbol{\mathcal{F'}})$
is another measurable space, a stochastic kernel on
$(\boldsymbol{\Omega'},\boldsymbol{\mathcal{F'}})$
is another measurable space, a stochastic kernel on
![]() $\boldsymbol{\Omega'}$
given
$\boldsymbol{\Omega'}$
given
![]() $\boldsymbol{\Omega}$
is a mapping
$\boldsymbol{\Omega}$
is a mapping
![]() $Q\,:\,\boldsymbol{\Omega}\times\boldsymbol{\mathcal{F'}}\rightarrow[0, 1]$
such that
$Q\,:\,\boldsymbol{\Omega}\times\boldsymbol{\mathcal{F'}}\rightarrow[0, 1]$
such that
![]() $\omega\mapsto Q(B|\omega)$
is measurable on
$\omega\mapsto Q(B|\omega)$
is measurable on
![]() $(\boldsymbol{\Omega},\boldsymbol{\mathcal{F}})$
for every
$(\boldsymbol{\Omega},\boldsymbol{\mathcal{F}})$
for every
![]() $B\in\boldsymbol{\mathcal{F}}'$
, and
$B\in\boldsymbol{\mathcal{F}}'$
, and
![]() $B\mapsto Q(B|\omega)$
is in
$B\mapsto Q(B|\omega)$
is in
![]() $\boldsymbol{\mathcal{P}}(\boldsymbol{\Omega'})$
for every
$\boldsymbol{\mathcal{P}}(\boldsymbol{\Omega'})$
for every
![]() $\omega\in\boldsymbol{\Omega}$
. We denote by
$\omega\in\boldsymbol{\Omega}$
. We denote by
![]() $\boldsymbol{\mathcal{B}}(\boldsymbol{\Omega})$
the family of bounded measurable functions
$\boldsymbol{\mathcal{B}}(\boldsymbol{\Omega})$
the family of bounded measurable functions
![]() $f\,:\,\boldsymbol{\Omega}\rightarrow\mathbb{R}$
(here,
$f\,:\,\boldsymbol{\Omega}\rightarrow\mathbb{R}$
(here,
![]() $\mathbb{R}$
is endowed with its Borel
$\mathbb{R}$
is endowed with its Borel
![]() $\sigma$
-algebra). If Q is a stochastic kernel on
$\sigma$
-algebra). If Q is a stochastic kernel on
![]() $\boldsymbol{\Omega'}$
given
$\boldsymbol{\Omega'}$
given
![]() $\boldsymbol{\Omega}$
and f is a real-valued measurable function on
$\boldsymbol{\Omega}$
and f is a real-valued measurable function on
![]() $\boldsymbol{\Omega'}$
, allowed to take infinite values, we will denote by Qf the
$\boldsymbol{\Omega'}$
, allowed to take infinite values, we will denote by Qf the
![]() $\boldsymbol{\mathcal{F}}$
-measurable function defined by the following (provided that the integral is well defined):
$\boldsymbol{\mathcal{F}}$
-measurable function defined by the following (provided that the integral is well defined):
In general, for a product of measurable spaces we will always consider the product
![]() $\sigma$
-algebra. The indicator function of a set
$\sigma$
-algebra. The indicator function of a set
![]() $C\in\boldsymbol{\mathcal{F}}$
is written
$C\in\boldsymbol{\mathcal{F}}$
is written
![]() $\textbf{I}_C$
.
$\textbf{I}_C$
.
Throughout this paper, any metric space
![]() $\textbf{S}$
will be endowed with its Borel
$\textbf{S}$
will be endowed with its Borel
![]() $\sigma$
-algebra
$\sigma$
-algebra
![]() $\boldsymbol{\mathfrak{B}}(\textbf{S})$
. Also, when considering the product of a finite family of metric spaces, we will consider the product topology (which makes the product again a metric space). By
$\boldsymbol{\mathfrak{B}}(\textbf{S})$
. Also, when considering the product of a finite family of metric spaces, we will consider the product topology (which makes the product again a metric space). By
![]() $\boldsymbol{\mathcal{C}}(\textbf{S})$
we will denote the family of bounded continuous functions
$\boldsymbol{\mathcal{C}}(\textbf{S})$
we will denote the family of bounded continuous functions
![]() $f\,:\,\boldsymbol{\textbf{S}}\rightarrow\mathbb{R}$
. Let
$f\,:\,\boldsymbol{\textbf{S}}\rightarrow\mathbb{R}$
. Let
![]() $(\boldsymbol{\Omega},\boldsymbol{\mathcal{F}})$
be a measurable space and
$(\boldsymbol{\Omega},\boldsymbol{\mathcal{F}})$
be a measurable space and
![]() $\textbf{S}$
a metric space. We say that
$\textbf{S}$
a metric space. We say that
![]() $f\,:\, \boldsymbol{\Omega}\times \textbf{S}\rightarrow\mathbb{R}$
is a Carathéodory function if
$f\,:\, \boldsymbol{\Omega}\times \textbf{S}\rightarrow\mathbb{R}$
is a Carathéodory function if
![]() $f(\omega,\cdot)$
is continuous on
$f(\omega,\cdot)$
is continuous on
![]() $\textbf{S}$
for every
$\textbf{S}$
for every
![]() $\omega\in \boldsymbol{\Omega}$
, and
$\omega\in \boldsymbol{\Omega}$
, and
![]() $f(\cdot,s)$
is an
$f(\cdot,s)$
is an
![]() $\boldsymbol{\mathcal{F}}$
-measurable function for every
$\boldsymbol{\mathcal{F}}$
-measurable function for every
![]() $s\in\textbf{S}$
. The family of Carathéodory functions thus defined is denoted by
$s\in\textbf{S}$
. The family of Carathéodory functions thus defined is denoted by
![]() ${\textit{Car}}(\boldsymbol{\Omega}\times \textbf{S})$
. The family of Carathéodory functions which, in addition, are bounded is denoted by
${\textit{Car}}(\boldsymbol{\Omega}\times \textbf{S})$
. The family of Carathéodory functions which, in addition, are bounded is denoted by
![]() ${\textit{Car}}_{b}(\boldsymbol{\Omega}\times \textbf{S})$
. When the metric space
${\textit{Car}}_{b}(\boldsymbol{\Omega}\times \textbf{S})$
. When the metric space
![]() $\textbf{S}$
is separable, any
$\textbf{S}$
is separable, any
![]() $f\in{\textit{Car}}(\boldsymbol{\Omega}\times \textbf{S})$
is a jointly measurable function on
$f\in{\textit{Car}}(\boldsymbol{\Omega}\times \textbf{S})$
is a jointly measurable function on
![]() $(\boldsymbol{\Omega}\times\textbf{S},\boldsymbol{\mathcal{F}}\otimes\boldsymbol{\mathfrak{B}}(\textbf{S}))$
. The Dirac probability measure
$(\boldsymbol{\Omega}\times\textbf{S},\boldsymbol{\mathcal{F}}\otimes\boldsymbol{\mathfrak{B}}(\textbf{S}))$
. The Dirac probability measure
![]() $\delta_s\in\boldsymbol{\mathcal{P}}(\textbf{S})$
concentrated at some
$\delta_s\in\boldsymbol{\mathcal{P}}(\textbf{S})$
concentrated at some
![]() $s\in\textbf{S}$
is given by
$s\in\textbf{S}$
is given by
![]() $B\mapsto \textbf{I}_B(s)$
for
$B\mapsto \textbf{I}_B(s)$
for
![]() $B\in\boldsymbol{\mathfrak{B}}(\textbf{S})$
.
$B\in\boldsymbol{\mathfrak{B}}(\textbf{S})$
.
Given
![]() $\lambda\in\boldsymbol{\mathcal{P}}(\textbf{S})$
, let
$\lambda\in\boldsymbol{\mathcal{P}}(\textbf{S})$
, let
![]() $L^1(\textbf{S},\boldsymbol{\mathfrak{B}}(\textbf{S}),\lambda)$
be the family of real-valued measurable functions on
$L^1(\textbf{S},\boldsymbol{\mathfrak{B}}(\textbf{S}),\lambda)$
be the family of real-valued measurable functions on
![]() $\textbf{S}$
which are
$\textbf{S}$
which are
![]() $\lambda$
-integrable (as usual, functions which are equal
$\lambda$
-integrable (as usual, functions which are equal
![]() $\lambda$
-almost everywhere are identified). With the usual definition of the 1-norm, we have that
$\lambda$
-almost everywhere are identified). With the usual definition of the 1-norm, we have that
![]() $L^1(\textbf{S},\boldsymbol{\mathfrak{B}}(\textbf{S}),\lambda)$
is a Banach space and convergence in norm is
$L^1(\textbf{S},\boldsymbol{\mathfrak{B}}(\textbf{S}),\lambda)$
is a Banach space and convergence in norm is
The family of
![]() $\lambda$
-essentially bounded measurable functions is
$\lambda$
-essentially bounded measurable functions is
![]() $L^\infty(\textbf{S},\boldsymbol{\mathfrak{B}}(\textbf{S}),\lambda)$
, and the essential supremum norm in
$L^\infty(\textbf{S},\boldsymbol{\mathfrak{B}}(\textbf{S}),\lambda)$
, and the essential supremum norm in
![]() $L^\infty$
is denoted by
$L^\infty$
is denoted by
![]() $\|\cdot\|$
. The weak
$\|\cdot\|$
. The weak
![]() $^{*}$
topology on the space
$^{*}$
topology on the space
![]() $L^{\infty}(\textbf{S},\boldsymbol{\mathfrak{B}}(\textbf{S}),\lambda)$
, denoted by
$L^{\infty}(\textbf{S},\boldsymbol{\mathfrak{B}}(\textbf{S}),\lambda)$
, denoted by
![]() $\sigma(L^{\infty}(\textbf{S},\boldsymbol{\mathfrak{B}}(\textbf{S}),\lambda),L^{1}(\textbf{S},\boldsymbol{\mathfrak{B}}(\textbf{S}),\lambda))$
, is the coarsest topology for which the mappings
$\sigma(L^{\infty}(\textbf{S},\boldsymbol{\mathfrak{B}}(\textbf{S}),\lambda),L^{1}(\textbf{S},\boldsymbol{\mathfrak{B}}(\textbf{S}),\lambda))$
, is the coarsest topology for which the mappings
are continuous. We will write
![]() $f_n\ {\stackrel{*}{\rightharpoonup}\ } f$
when
$f_n\ {\stackrel{*}{\rightharpoonup}\ } f$
when
The rest of the paper is organized as follows. In Section 2, we define the original control model
![]() $\mathcal{M}$
and state some important preliminary results, the proof of one of these results being postponed to Appendix A, at the end of the paper. A family of auxiliary MDPs
$\mathcal{M}$
and state some important preliminary results, the proof of one of these results being postponed to Appendix A, at the end of the paper. A family of auxiliary MDPs
![]() $\mathcal{M}_{\beta}$
, parametrized by
$\mathcal{M}_{\beta}$
, parametrized by
![]() $0<\beta<1$
, is introduced in Section 3. The main results of the paper are given in Section 4.
$0<\beta<1$
, is introduced in Section 3. The main results of the paper are given in Section 4.
2. Definition of the control model
 $\mathcal{M}$
$\mathcal{M}$
Elements of the control model
![]() $\mathcal{M}$
.
$\mathcal{M}$
.
The MDP under consideration consists of the following elements:
-
The state space
 $\textbf{X}$
and the action space
$\textbf{X}$
and the action space
 $\textbf{A}$
are both Borel spaces endowed with their respective Borel
$\textbf{A}$
are both Borel spaces endowed with their respective Borel
 $\sigma$
-algebras
$\sigma$
-algebras
 $\boldsymbol{\mathfrak{B}}(\textbf{X})$
and
$\boldsymbol{\mathfrak{B}}(\textbf{X})$
and
 $\boldsymbol{\mathfrak{B}}(\textbf{A})$
.
$\boldsymbol{\mathfrak{B}}(\textbf{A})$
. -
For each
 $x\in\textbf{X}$
, the nonempty measurable set
$x\in\textbf{X}$
, the nonempty measurable set
 $\textbf{A}(x)\subseteq \textbf{A}$
stands for the set of available actions in state x. Let
$\textbf{A}(x)\subseteq \textbf{A}$
stands for the set of available actions in state x. Let
 $\textbf{K}=\{(x,a)\in\textbf{X}\times\textbf{A}\,:\, a\in \textbf{A}(x)\}$
be the family of feasible state–action pairs. Assumption (A.1) below will ensure that
$\textbf{K}=\{(x,a)\in\textbf{X}\times\textbf{A}\,:\, a\in \textbf{A}(x)\}$
be the family of feasible state–action pairs. Assumption (A.1) below will ensure that
 $\textbf{K}\in\boldsymbol{\mathfrak{B}}(\textbf{X})\otimes\boldsymbol{\mathfrak{B}}(\textbf{A})$
.
$\textbf{K}\in\boldsymbol{\mathfrak{B}}(\textbf{X})\otimes\boldsymbol{\mathfrak{B}}(\textbf{A})$
. -
The initial distribution of the system is the probability measure
 $\nu\in\boldsymbol{\mathcal{P}}(\textbf{X})$
, and the transitions of the system are given by a stochastic kernel Q on
$\nu\in\boldsymbol{\mathcal{P}}(\textbf{X})$
, and the transitions of the system are given by a stochastic kernel Q on
 $\textbf{X}$
given
$\textbf{X}$
given
 $\textbf{K}$
.
$\textbf{K}$
. -
Finally, regarding the performance criterion to be optimized (which we will define later), a nontrivial measurable subset of the state space
 $G\subseteq\textbf{X}$
is given.
$G\subseteq\textbf{X}$
is given.
Our main conditions on the control model
![]() $\mathcal{M}$
are stated next. In Assumption (A.2) we introduce a reference probability measure
$\mathcal{M}$
are stated next. In Assumption (A.2) we introduce a reference probability measure
![]() $\lambda\in\boldsymbol{\mathcal{P}}(\textbf{X})$
.
$\lambda\in\boldsymbol{\mathcal{P}}(\textbf{X})$
.
Assumption A.
-
(A.1) The action set
 $\textbf{A}$
is compact, and the correspondence from
$\textbf{A}$
is compact, and the correspondence from
 $\textbf{X}$
to subsets of
$\textbf{X}$
to subsets of
 $\textbf{A}$
defined by
$\textbf{A}$
defined by
 $x\mapsto \textbf{A}(x)$
is weakly measurable with nonempty compact values (see Definition 18.1 in [Reference Aliprantis and Border1]).
$x\mapsto \textbf{A}(x)$
is weakly measurable with nonempty compact values (see Definition 18.1 in [Reference Aliprantis and Border1]). -
(A.2) There exist a reference probability measure
 $\lambda\in\boldsymbol{\mathcal{P}}(\textbf{X})$
and a measurable function
$\lambda\in\boldsymbol{\mathcal{P}}(\textbf{X})$
and a measurable function
 $q\,:\, \textbf{K}\times\textbf{X}\rightarrow\mathbb{R}^+$
such that for every
$q\,:\, \textbf{K}\times\textbf{X}\rightarrow\mathbb{R}^+$
such that for every
 $D\in\boldsymbol{\mathfrak{B}}(\textbf{X})$
and every
$D\in\boldsymbol{\mathfrak{B}}(\textbf{X})$
and every
 $(x,a)\in\textbf{K}$
, (2.1)Also, for every
$(x,a)\in\textbf{K}$
, (2.1)Also, for every \begin{align}Q(D|x,a)=\int_D q(x,a,y)\lambda(dy).\end{align}
\begin{align}Q(D|x,a)=\int_D q(x,a,y)\lambda(dy).\end{align}
 $x\in\textbf{X}$
we have the following continuity condition:
$x\in\textbf{X}$
we have the following continuity condition:  \begin{align*}\lim_{k\rightarrow\infty} \int_{\textbf{X}} |q(x,b_{k},y)-q(x,b,y)| \lambda(dy)=0\quad\hbox{whenever $b_k\rightarrow b$ in $\textbf{A}(x)$}. \end{align*}
\begin{align*}\lim_{k\rightarrow\infty} \int_{\textbf{X}} |q(x,b_{k},y)-q(x,b,y)| \lambda(dy)=0\quad\hbox{whenever $b_k\rightarrow b$ in $\textbf{A}(x)$}. \end{align*}
-
(A.3) The initial distribution
 $\nu$
is absolutely continuous with respect to
$\nu$
is absolutely continuous with respect to
 $\lambda$
in Assumption (A.2).
$\lambda$
in Assumption (A.2).
Remark 2.1.
-
(a) Under Assumption (A.1), and as a consequence of Theorem 18.6 in [Reference Aliprantis and Border1], we have that
 $\textbf{K}$
is indeed a measurable subset of
$\textbf{K}$
is indeed a measurable subset of
 $\textbf{X}\times\textbf{A}$
.
$\textbf{X}\times\textbf{A}$
. -
(b) The continuity condition in Assumption (A.2) can equivalently be written as
 \begin{align*}q(x,b_k,\cdot)\stackrel{L^1}{\longrightarrow} q(x,b,\cdot)\quad \textrm{for any}\ x\in\textbf{X}\ \textrm{when}\ b_k\rightarrow b\ \textrm{in}\ \textbf{A}(x).\end{align*}
\begin{align*}q(x,b_k,\cdot)\stackrel{L^1}{\longrightarrow} q(x,b,\cdot)\quad \textrm{for any}\ x\in\textbf{X}\ \textrm{when}\ b_k\rightarrow b\ \textrm{in}\ \textbf{A}(x).\end{align*}
-
(c) The condition in Assumption (A.3) is not restrictive at all. Indeed, if it were not true that
 $\nu\ll\lambda$
, then we would consider the reference probability measure
$\nu\ll\lambda$
, then we would consider the reference probability measure
 $\eta=\frac{1}{2}(\nu+\lambda)$
in Assumption (A.2), so that (2.1) would become and the continuity condition would be satisfied as well.
$\eta=\frac{1}{2}(\nu+\lambda)$
in Assumption (A.2), so that (2.1) would become and the continuity condition would be satisfied as well. \begin{align*}Q(D|x,a)=\int_D q(x,a,y)\frac{d\lambda}{d\eta}(y)\,\eta(dy)\end{align*}
\begin{align*}Q(D|x,a)=\int_D q(x,a,y)\frac{d\lambda}{d\eta}(y)\,\eta(dy)\end{align*}
-
(d) The fact that
 $\textbf{X}$
is a Borel space will be used to ensure that the
$\textbf{X}$
is a Borel space will be used to ensure that the
 $ws^\infty$
-topology on the set of strategic measures (details will be given below) coincides with the weak topology—see [Reference Balder3, Reference Nowak23]—and that the set of strategic probability measures is compact with this topology. Otherwise, no topological properties of
$ws^\infty$
-topology on the set of strategic measures (details will be given below) coincides with the weak topology—see [Reference Balder3, Reference Nowak23]—and that the set of strategic probability measures is compact with this topology. Otherwise, no topological properties of
 $\textbf{X}$
will be used.
$\textbf{X}$
will be used.
Control policies. The space of admissible histories up to time n for the controlled process is denoted by
![]() $\textbf{H}_{n}$
for
$\textbf{H}_{n}$
for
![]() $n\in\mathbb{N}$
. It is defined recursively by
$n\in\mathbb{N}$
. It is defined recursively by
![]() $\textbf{H}_0=\textbf{X}$
and
$\textbf{H}_0=\textbf{X}$
and
![]() $\textbf{H}_n=\textbf{K}\times\textbf{H}_{n-1}$
for any
$\textbf{H}_n=\textbf{K}\times\textbf{H}_{n-1}$
for any
![]() $n\ge1$
, and it is endowed with the corresponding product
$n\ge1$
, and it is endowed with the corresponding product
![]() $\sigma$
-algebra. A control policy
$\sigma$
-algebra. A control policy
![]() $\pi$
is a sequence
$\pi$
is a sequence
![]() $\{\pi_n\}_{n\ge0}$
of stochastic kernels on
$\{\pi_n\}_{n\ge0}$
of stochastic kernels on
![]() $\textbf{A}$
given
$\textbf{A}$
given
![]() $\textbf{H}_n$
, denoted by
$\textbf{H}_n$
, denoted by
![]() $\pi_n(da|h_n)$
, such that for each
$\pi_n(da|h_n)$
, such that for each
![]() $n\ge0$
and
$n\ge0$
and
![]() $h_n=(x_0,a_0,\ldots,x_n)\in\textbf{H}_n$
we have
$h_n=(x_0,a_0,\ldots,x_n)\in\textbf{H}_n$
we have
![]() $\pi_n(\textbf{A}(x_n)|h_n)=1$
. The set of all policies is denoted by
$\pi_n(\textbf{A}(x_n)|h_n)=1$
. The set of all policies is denoted by
![]() $\boldsymbol{\Pi}$
.
$\boldsymbol{\Pi}$
.
Dynamics of the control model. The canonical sample space of all possible state and actions is
![]() $\boldsymbol{\Omega}=(\textbf{X}\times\textbf{A})^\infty$
, and it is endowed with the product
$\boldsymbol{\Omega}=(\textbf{X}\times\textbf{A})^\infty$
, and it is endowed with the product
![]() $\sigma$
-algebra
$\sigma$
-algebra
![]() $\boldsymbol{\mathcal{F}}$
. Thus, a generic element
$\boldsymbol{\mathcal{F}}$
. Thus, a generic element
![]() $\omega\in\boldsymbol{\Omega}$
consists of a sequence of the form
$\omega\in\boldsymbol{\Omega}$
consists of a sequence of the form
![]() $(x_0,a_0,x_1,a_1,\ldots)$
, where
$(x_0,a_0,x_1,a_1,\ldots)$
, where
![]() $x_{n}\in \textbf{X}$
and
$x_{n}\in \textbf{X}$
and
![]() $a_{n}\in\textbf{A}$
for any
$a_{n}\in\textbf{A}$
for any
![]() $n\in\mathbb{N}$
. For
$n\in\mathbb{N}$
. For
![]() $n\in\mathbb{N}$
, the projection functions
$n\in\mathbb{N}$
, the projection functions
![]() $X_{n}$
and
$X_{n}$
and
![]() $A_{n}$
from
$A_{n}$
from
![]() $\boldsymbol{\Omega}$
to
$\boldsymbol{\Omega}$
to
![]() $\textbf{X}$
and
$\textbf{X}$
and
![]() $\textbf{A}$
respectively are defined by
$\textbf{A}$
respectively are defined by
![]() $X_{n}(\omega)= x_{n}$
and
$X_{n}(\omega)= x_{n}$
and
![]() $A_{n}(\omega)= a_{n}$
for
$A_{n}(\omega)= a_{n}$
for
![]() $\omega=(x_0,a_0,\ldots,x_n,a_n,\ldots)$
, and they are called the state and control variables at time n. The history process up to time n is denoted by
$\omega=(x_0,a_0,\ldots,x_n,a_n,\ldots)$
, and they are called the state and control variables at time n. The history process up to time n is denoted by
![]() $H_n=(X_0,A_0,\ldots,X_n)$
.
$H_n=(X_0,A_0,\ldots,X_n)$
.
For any policy
![]() $\pi\in\boldsymbol{\Pi}$
, there exists a unique probability measure
$\pi\in\boldsymbol{\Pi}$
, there exists a unique probability measure
![]() $\mathbb{P}^{\pi}_{\nu}$
on
$\mathbb{P}^{\pi}_{\nu}$
on
![]() $(\boldsymbol{\Omega},\boldsymbol{\mathcal{F}})$
supported on
$(\boldsymbol{\Omega},\boldsymbol{\mathcal{F}})$
supported on
![]() $\textbf{K}^\infty$
(that is,
$\textbf{K}^\infty$
(that is,
![]() $\mathbb{P}^{\pi}_{\nu}( \textbf{K}^\infty)=1)$
which satisfies the following conditions:
$\mathbb{P}^{\pi}_{\nu}( \textbf{K}^\infty)=1)$
which satisfies the following conditions:
-
(i) We have
 $\mathbb{P}^{\pi}_{\nu} \{X_0\in D\}=\nu(D)$
for any
$\mathbb{P}^{\pi}_{\nu} \{X_0\in D\}=\nu(D)$
for any
 $D\in \boldsymbol{\mathfrak{B}}(\textbf{X})$
.
$D\in \boldsymbol{\mathfrak{B}}(\textbf{X})$
. -
(ii) For any
 $n\ge0$
and
$n\ge0$
and
 $C\in\boldsymbol{\mathfrak{B}}(\textbf{A})$
we have
$C\in\boldsymbol{\mathfrak{B}}(\textbf{A})$
we have
 $\mathbb{P}^{\pi}_{\nu}\{ A_n\in C | H_n\} = \pi_n(C|H_n)$
.
$\mathbb{P}^{\pi}_{\nu}\{ A_n\in C | H_n\} = \pi_n(C|H_n)$
. -
(iii) For any
 $n\ge0$
and
$n\ge0$
and
 $D\in\boldsymbol{\mathfrak{B}}(\textbf{X})$
we have
$D\in\boldsymbol{\mathfrak{B}}(\textbf{X})$
we have
 $\mathbb{P}^{\pi}_{\nu}\{ X_{n+1}\in D| H_n,A_n\}=Q(D | X_n,A_n)$
.
$\mathbb{P}^{\pi}_{\nu}\{ X_{n+1}\in D| H_n,A_n\}=Q(D | X_n,A_n)$
.
The probability measure
![]() $\mathbb{P}^{\pi}_{\nu}$
is usually referred to as a strategic probability measure. The corresponding expectation operator is
$\mathbb{P}^{\pi}_{\nu}$
is usually referred to as a strategic probability measure. The corresponding expectation operator is
![]() $\mathbb{E}^{\pi}_{\nu}$
. The set of all strategic probability measures
$\mathbb{E}^{\pi}_{\nu}$
. The set of all strategic probability measures
![]() $\{\mathbb{P}^{\pi}_{\nu}\}_{\pi\in\boldsymbol{\Pi}}$
is denoted by
$\{\mathbb{P}^{\pi}_{\nu}\}_{\pi\in\boldsymbol{\Pi}}$
is denoted by
![]() $\boldsymbol{\mathcal{S}}_{\nu}\subseteq\boldsymbol{\mathcal{P}}(\boldsymbol{\Omega})$
.
$\boldsymbol{\mathcal{S}}_{\nu}\subseteq\boldsymbol{\mathcal{P}}(\boldsymbol{\Omega})$
.
We will also denote by
![]() $\mathbb{P}^\pi_{\nu,n}$
the distribution of the random variable
$\mathbb{P}^\pi_{\nu,n}$
the distribution of the random variable
![]() $H_n$
; more formally, for any
$H_n$
; more formally, for any
![]() $n\ge0$
we define
$n\ge0$
we define
![]() $\mathbb{P}^\pi_{\nu,n}$
as the pushforward probability measure on
$\mathbb{P}^\pi_{\nu,n}$
as the pushforward probability measure on
![]() $(\textbf{X}\times\textbf{A})^n\times\textbf{X}$
given by
$(\textbf{X}\times\textbf{A})^n\times\textbf{X}$
given by
![]() $\mathbb{P}^\pi_{\nu}\circ H_n^{-1}$
. Consequently, we have
$\mathbb{P}^\pi_{\nu}\circ H_n^{-1}$
. Consequently, we have
![]() $\mathbb{P}^\pi_{\nu,n}(\textbf{H}_n)=1$
; note also that
$\mathbb{P}^\pi_{\nu,n}(\textbf{H}_n)=1$
; note also that
![]() $\mathbb{P}^\pi_{\nu,0}=\nu$
.
$\mathbb{P}^\pi_{\nu,0}=\nu$
.
Optimality criterion. The performance criterion that we want to maximize is the probability of visiting the set G infinitely often. Let us denote by
![]() $N_{G}\,:\,\boldsymbol{\Omega}\rightarrow\mathbb{N}\cup\{\infty\}$
the integer-valued process that counts the total number of visits of the state process to the set G; that is,
$N_{G}\,:\,\boldsymbol{\Omega}\rightarrow\mathbb{N}\cup\{\infty\}$
the integer-valued process that counts the total number of visits of the state process to the set G; that is,
For notational convenience, if
![]() $I\subseteq\mathbb{N}$
is a set of decision epochs, we let
$I\subseteq\mathbb{N}$
is a set of decision epochs, we let
![]() $N_G(I)=\sum_{n\in I} \textbf{I}_{G}(X_n)$
, which stands for the number of visits to G at times in I.
$N_G(I)=\sum_{n\in I} \textbf{I}_{G}(X_n)$
, which stands for the number of visits to G at times in I.
For the initial distribution
![]() $\nu$
, the value function of the control model
$\nu$
, the value function of the control model
![]() $\mathcal{M}$
is given by
$\mathcal{M}$
is given by
A policy attaining the above supremum is said to be optimal. In the sequel, the model
![]() $\mathcal{M}$
introduced in this section will be referred to as the primary or original control problem.
$\mathcal{M}$
introduced in this section will be referred to as the primary or original control problem.
Stationary Markov policies. Let
![]() $\boldsymbol{\Pi}_{s}$
be the set of stochastic kernels
$\boldsymbol{\Pi}_{s}$
be the set of stochastic kernels
![]() $\pi$
on
$\pi$
on
![]() $\textbf{A}$
given
$\textbf{A}$
given
![]() $\textbf{X}$
such that
$\textbf{X}$
such that
![]() $\pi(\textbf{A}(x)|x)=1$
for each
$\pi(\textbf{A}(x)|x)=1$
for each
![]() $x\in\textbf{X}$
. We have that
$x\in\textbf{X}$
. We have that
![]() $\boldsymbol{\Pi}_{s}$
is nonempty as a consequence of our hypotheses. Indeed, from the Kuratowski–Ryll-Nardzewski selection theorem [Reference Aliprantis and Border1, Theorem 18.13] we derive the existence of a measurable selector for the correspondence
$\boldsymbol{\Pi}_{s}$
is nonempty as a consequence of our hypotheses. Indeed, from the Kuratowski–Ryll-Nardzewski selection theorem [Reference Aliprantis and Border1, Theorem 18.13] we derive the existence of a measurable selector for the correspondence
![]() $x\mapsto\textbf{A}(x)$
; that is, there exists a measurable
$x\mapsto\textbf{A}(x)$
; that is, there exists a measurable
![]() $f\,:\,\textbf{X}\rightarrow\textbf{A}$
such that
$f\,:\,\textbf{X}\rightarrow\textbf{A}$
such that
![]() $f(x)\in\textbf{A}(x)$
for every
$f(x)\in\textbf{A}(x)$
for every
![]() $x\in\textbf{X}$
. Then we have that
$x\in\textbf{X}$
. Then we have that
![]() $\pi(da|x)=\delta_{f(x)}(da)$
indeed belongs to
$\pi(da|x)=\delta_{f(x)}(da)$
indeed belongs to
![]() $\boldsymbol{\Pi}_{s}$
.
$\boldsymbol{\Pi}_{s}$
.
We say that
![]() $\{\pi_n\}_{n\in\mathbb{N}}\in\boldsymbol{\Pi}$
is a stationary Markov policy if there is some
$\{\pi_n\}_{n\in\mathbb{N}}\in\boldsymbol{\Pi}$
is a stationary Markov policy if there is some
![]() $\pi\in\boldsymbol{\Pi}_{s}$
such that
$\pi\in\boldsymbol{\Pi}_{s}$
such that
Without risk of confusion, we will identify the set of all stationary Markov policies with
![]() $\boldsymbol{\Pi}_{s}$
itself. The set of all strategic probability measures for the stationary Markov policies
$\boldsymbol{\Pi}_{s}$
itself. The set of all strategic probability measures for the stationary Markov policies
![]() $\{\mathbb{P}^{\pi}_{\nu}\}_{\pi\in\boldsymbol{\Pi}_s}$
is denoted by
$\{\mathbb{P}^{\pi}_{\nu}\}_{\pi\in\boldsymbol{\Pi}_s}$
is denoted by
![]() $\boldsymbol{\mathcal{S}}^s_{\nu}$
.
$\boldsymbol{\mathcal{S}}^s_{\nu}$
.
Lemma 2.1. If
![]() $\pi,\pi'\in\boldsymbol{\Pi}_s$
coincide
$\pi,\pi'\in\boldsymbol{\Pi}_s$
coincide
![]() $\lambda$
-almost everywhere (that is,
$\lambda$
-almost everywhere (that is,
![]() $\pi(da|x)=\pi'(da|x)$
for all x in a set of
$\pi(da|x)=\pi'(da|x)$
for all x in a set of
![]() $\lambda$
-probability one), then
$\lambda$
-probability one), then
![]() $\mathbb{P}^{\pi}_{\nu}=\mathbb{P}^{\pi'}_{\nu}$
.
$\mathbb{P}^{\pi}_{\nu}=\mathbb{P}^{\pi'}_{\nu}$
.
Proof. Suppose that
![]() $Y\in\boldsymbol{\mathfrak{B}}(\textbf{X})$
with
$Y\in\boldsymbol{\mathfrak{B}}(\textbf{X})$
with
![]() $\lambda(Y)=1$
is such that
$\lambda(Y)=1$
is such that
![]() $\pi(da|x)=\pi'(da|x)$
for every
$\pi(da|x)=\pi'(da|x)$
for every
![]() $x\in Y$
. We will prove by induction on
$x\in Y$
. We will prove by induction on
![]() $n\ge0$
that
$n\ge0$
that
![]() $(X_0,A_0,\ldots,X_n,A_n)$
has the same distribution under
$(X_0,A_0,\ldots,X_n,A_n)$
has the same distribution under
![]() $\mathbb{P}^{\pi}_{\nu}$
and under
$\mathbb{P}^{\pi}_{\nu}$
and under
![]() $\mathbb{P}^{\pi'}_{\nu}$
. Letting
$\mathbb{P}^{\pi'}_{\nu}$
. Letting
![]() $n=0$
, and given
$n=0$
, and given
![]() $D\in\boldsymbol{\mathfrak{B}}(\textbf{X})$
and
$D\in\boldsymbol{\mathfrak{B}}(\textbf{X})$
and
![]() $C\in\boldsymbol{\mathfrak{B}}(\textbf{A})$
, we have
$C\in\boldsymbol{\mathfrak{B}}(\textbf{A})$
, we have
 \begin{eqnarray*}\mathbb{P}^\pi_{\nu}\{X_0\in D,A_0\in C\} &=& \, \int_D \pi(C|x)\frac{d\nu}{d\lambda}(x)\, \lambda(dx)\ =\ \int_{D\cap Y} \pi(C|x)\frac{d\nu}{d\lambda}(x)\, \lambda(dx) \\&=& \, \int_{D} \pi'(C|x)\frac{d\nu}{d\lambda}(x)\, \lambda(dx) \ =\ \mathbb{P}^{\pi'}_{\nu}\{X_0\in D,A_0\in C\}.\end{eqnarray*}
\begin{eqnarray*}\mathbb{P}^\pi_{\nu}\{X_0\in D,A_0\in C\} &=& \, \int_D \pi(C|x)\frac{d\nu}{d\lambda}(x)\, \lambda(dx)\ =\ \int_{D\cap Y} \pi(C|x)\frac{d\nu}{d\lambda}(x)\, \lambda(dx) \\&=& \, \int_{D} \pi'(C|x)\frac{d\nu}{d\lambda}(x)\, \lambda(dx) \ =\ \mathbb{P}^{\pi'}_{\nu}\{X_0\in D,A_0\in C\}.\end{eqnarray*}
Assuming the result is true for
![]() $n\ge0$
, and again letting
$n\ge0$
, and again letting
![]() $D\in\boldsymbol{\mathfrak{B}}(\textbf{X})$
and
$D\in\boldsymbol{\mathfrak{B}}(\textbf{X})$
and
![]() $C\in\boldsymbol{\mathfrak{B}}(\textbf{A})$
, we have
$C\in\boldsymbol{\mathfrak{B}}(\textbf{A})$
, we have
which, by the same argument, is equal to
![]() $\mathbb{P}^{\pi'}_{\nu}\{ X_{n+1}\in D, A_{n+1}\in C\mid X_n=x,A_n=a\}$
. The conditional distributions and the distribution of
$\mathbb{P}^{\pi'}_{\nu}\{ X_{n+1}\in D, A_{n+1}\in C\mid X_n=x,A_n=a\}$
. The conditional distributions and the distribution of
![]() $(X_n,A_n)$
being the same under
$(X_n,A_n)$
being the same under
![]() $\pi$
and
$\pi$
and
![]() $\pi'$
, we conclude the result.
$\pi'$
, we conclude the result.
Remark 2.2. It turns out that two stationary Markov policies under the conditions of Lemma 2.1, i.e., which coincide
![]() $\lambda$
-almost surely, are indistinguishable, since they yield the same strategic probability measure; in addition, they have the same performance (recall (2.2)), since the criterion to be maximized depends on the strategic probability measures.
$\lambda$
-almost surely, are indistinguishable, since they yield the same strategic probability measure; in addition, they have the same performance (recall (2.2)), since the criterion to be maximized depends on the strategic probability measures.
Young measures. Let
![]() $\boldsymbol{\mathcal{R}}\supseteq\boldsymbol{\Pi}_s$
be the set of stochastic kernels
$\boldsymbol{\mathcal{R}}\supseteq\boldsymbol{\Pi}_s$
be the set of stochastic kernels
![]() $\gamma$
on
$\gamma$
on
![]() $\textbf{A}$
given
$\textbf{A}$
given
![]() $\textbf{X}$
such that
$\textbf{X}$
such that
![]() $\gamma(\textbf{A}(x)|x)=1$
for
$\gamma(\textbf{A}(x)|x)=1$
for
![]() $\lambda$
-almost every
$\lambda$
-almost every
![]() $x\in\textbf{X}$
. On
$x\in\textbf{X}$
. On
![]() $\boldsymbol{\mathcal{R}}$
we consider the equivalence relation
$\boldsymbol{\mathcal{R}}$
we consider the equivalence relation
![]() $\approx$
defined as
$\approx$
defined as
![]() $\gamma\approx\gamma'$
when
$\gamma\approx\gamma'$
when
![]() $\gamma(\cdot|x)=\gamma'(\cdot|x)$
for
$\gamma(\cdot|x)=\gamma'(\cdot|x)$
for
![]() $\lambda$
-almost all
$\lambda$
-almost all
![]() $x\in\textbf{X}$
. The corresponding quotient space
$x\in\textbf{X}$
. The corresponding quotient space
![]() $\boldsymbol{\mathcal{R}}\,/\approx$
, denoted by
$\boldsymbol{\mathcal{R}}\,/\approx$
, denoted by
![]() $\boldsymbol{\mathcal{Y}}$
, is the so-called set of Young measures. As a consequence of Lemma 2.1 and Remark 2.2, there is no loss of generality in identifying the set of stationary Markov policies
$\boldsymbol{\mathcal{Y}}$
, is the so-called set of Young measures. As a consequence of Lemma 2.1 and Remark 2.2, there is no loss of generality in identifying the set of stationary Markov policies
![]() $\boldsymbol{\Pi}_s$
with
$\boldsymbol{\Pi}_s$
with
![]() $\boldsymbol{\mathcal{Y}}$
, since all the elements in the same
$\boldsymbol{\mathcal{Y}}$
, since all the elements in the same
![]() $\approx$
-equivalence class have the same strategic probability measure. Thus we will indiscriminately use the symbols
$\approx$
-equivalence class have the same strategic probability measure. Thus we will indiscriminately use the symbols
![]() $\boldsymbol{\Pi}_s$
and
$\boldsymbol{\Pi}_s$
and
![]() $\boldsymbol{\mathcal{Y}}$
to refer to both the stationary Markov policies and the set of Young measures. Hence, we will write
$\boldsymbol{\mathcal{Y}}$
to refer to both the stationary Markov policies and the set of Young measures. Hence, we will write
The set of Young measures
![]() $\boldsymbol{\mathcal{Y}}$
will be equipped with the narrow (stable) topology. This is the coarsest topology which makes the following mappings continuous:
$\boldsymbol{\mathcal{Y}}$
will be equipped with the narrow (stable) topology. This is the coarsest topology which makes the following mappings continuous:
for any
![]() $f\in {\textit{Car}}(\textbf{X}\times\textbf{A})$
such that for some
$f\in {\textit{Car}}(\textbf{X}\times\textbf{A})$
such that for some
![]() $\Phi$
in
$\Phi$
in
![]() $L^1(\textbf{X},\boldsymbol{\mathfrak{B}}(\textbf{X}),\lambda)$
we have
$L^1(\textbf{X},\boldsymbol{\mathfrak{B}}(\textbf{X}),\lambda)$
we have
![]() $|f(x,a)| \leq \Phi(x)$
for every
$|f(x,a)| \leq \Phi(x)$
for every
![]() $(x,a)\in\textbf{X}\times\textbf{A}$
; see [Reference Balder2, Theorem 2.2]. By [Reference Balder4, Lemma 1], the set
$(x,a)\in\textbf{X}\times\textbf{A}$
; see [Reference Balder2, Theorem 2.2]. By [Reference Balder4, Lemma 1], the set
![]() $\boldsymbol{\mathcal{Y}}$
endowed with the narrow topology becomes a compact metric space. We state this result in the next lemma.
$\boldsymbol{\mathcal{Y}}$
endowed with the narrow topology becomes a compact metric space. We state this result in the next lemma.
Lemma 2.2. Under Assumption A, the sets
![]() $\boldsymbol{\mathcal{Y}}$
of Young measures and
$\boldsymbol{\mathcal{Y}}$
of Young measures and
![]() $\boldsymbol{\Pi}_s$
of stationary Markov policies are compact metric spaces when endowed with the narrow topology.
$\boldsymbol{\Pi}_s$
of stationary Markov policies are compact metric spaces when endowed with the narrow topology.
The
![]() $ws^\infty$
-topology. Finally, we introduce the so-called
$ws^\infty$
-topology. Finally, we introduce the so-called
![]() $ws^\infty$
-topology on
$ws^\infty$
-topology on
![]() $\boldsymbol{\mathcal{S}}_{\nu}$
. Let
$\boldsymbol{\mathcal{S}}_{\nu}$
. Let
where the arguments of
![]() $g\in\boldsymbol{\mathcal{U}}_n$
will be sorted as
$g\in\boldsymbol{\mathcal{U}}_n$
will be sorted as
![]() $(x_0,a_0,\ldots,x_{n-1},a_{n-1},x_{n})$
. The
$(x_0,a_0,\ldots,x_{n-1},a_{n-1},x_{n})$
. The
![]() $ws^\infty$
-topology on the set
$ws^\infty$
-topology on the set
![]() $\boldsymbol{\mathcal{S}}_{\nu}$
—see [Reference Schäl28]—is the smallest topology that makes the mappings
$\boldsymbol{\mathcal{S}}_{\nu}$
—see [Reference Schäl28]—is the smallest topology that makes the mappings
continuous for any
![]() $n\ge 0$
and
$n\ge 0$
and
![]() $g\in\boldsymbol{\mathcal{U}}_{n}$
. Therefore, a sequence
$g\in\boldsymbol{\mathcal{U}}_{n}$
. Therefore, a sequence
![]() $\{\mathbb{P}_k\}_{k\in\mathbb{N}}\subseteq\boldsymbol{\mathcal{S}}_{\nu}$
converges to
$\{\mathbb{P}_k\}_{k\in\mathbb{N}}\subseteq\boldsymbol{\mathcal{S}}_{\nu}$
converges to
![]() $\mathbb{P}\in\boldsymbol{\mathcal{S}}_{\nu}$
for the
$\mathbb{P}\in\boldsymbol{\mathcal{S}}_{\nu}$
for the
![]() $ws^\infty$
-topology, denoted by
$ws^\infty$
-topology, denoted by
![]() $\mathbb{P}_k\Rightarrow \mathbb{P}$
, if and only if
$\mathbb{P}_k\Rightarrow \mathbb{P}$
, if and only if
for any
![]() $n\in\mathbb{N}$
and
$n\in\mathbb{N}$
and
![]() $g\in\boldsymbol{\mathcal{U}}_{n}$
.
$g\in\boldsymbol{\mathcal{U}}_{n}$
.
The proof of Lemmas 2.3 and Theorem 2.1 below are fairly involved; they are presented in Appendix A. Note that Lemma 2.3 simply states that the mapping that associates to a Young measure its corresponding strategic probability measure is continuous.
Lemma 2.3. Suppose that Assumption A holds. If
![]() $\{\pi_k\}_{k\in\mathbb{N}}$
and
$\{\pi_k\}_{k\in\mathbb{N}}$
and
![]() $\pi$
in
$\pi$
in
![]() $\boldsymbol{\mathcal{Y}}$
are such that
$\boldsymbol{\mathcal{Y}}$
are such that
![]() $\pi_k\rightarrow\pi$
, then
$\pi_k\rightarrow\pi$
, then
![]() $\mathbb{P}^{\pi_k}_{\nu}\Rightarrow\mathbb{P}^\pi_{\nu}$
.
$\mathbb{P}^{\pi_k}_{\nu}\Rightarrow\mathbb{P}^\pi_{\nu}$
.
Theorem 2.1. Under Assumption A, the sets
![]() $\boldsymbol{\mathcal{S}}_{\nu}$
and
$\boldsymbol{\mathcal{S}}_{\nu}$
and
![]() $\boldsymbol{\mathcal{S}}^s_{\nu}$
are compact metric spaces when endowed with the
$\boldsymbol{\mathcal{S}}^s_{\nu}$
are compact metric spaces when endowed with the
![]() $ws^\infty$
-topology.
$ws^\infty$
-topology.
It is worth mentioning that compactness of
![]() $\boldsymbol{\mathcal{S}}_{\nu}$
is a known result (see [Reference Balder3] or [Reference Schäl28]), whereas the new result that we establish here is compactness of
$\boldsymbol{\mathcal{S}}_{\nu}$
is a known result (see [Reference Balder3] or [Reference Schäl28]), whereas the new result that we establish here is compactness of
![]() $\boldsymbol{\mathcal{S}}^s_{\nu}$
.
$\boldsymbol{\mathcal{S}}^s_{\nu}$
.
3. The control model
 $\mathcal{M}_{\beta}$
$\mathcal{M}_{\beta}$
By its definition, the performance criterion introduced above is of asymptotic type, and it cannot be written in an additive form. Therefore, it appears difficult to study this type of control problem directly by using the traditional techniques, such as the dynamic programming or linear programming approach. To address this difficulty, we introduced in [Reference Dufour and Prieto-Rumeau15], in the particular context of a countable state space, an auxiliary model
![]() $\mathcal{M}_{\beta}$
as a tool for analyzing the original control problem.
$\mathcal{M}_{\beta}$
as a tool for analyzing the original control problem.
Elements of the control model
![]() $\mathcal{M}_{\beta}$
. Given
$\mathcal{M}_{\beta}$
. Given
![]() $0<\beta<1$
, the auxiliary control model
$0<\beta<1$
, the auxiliary control model
![]() $\mathcal{M}_{\beta}$
, which is based on the primary control model
$\mathcal{M}_{\beta}$
, which is based on the primary control model
![]() $\mathcal{M}$
, is a ‘total-expected-reward’ MDP defined as follows:
$\mathcal{M}$
, is a ‘total-expected-reward’ MDP defined as follows:
-
The state and action spaces are augmented with isolated points,
so that \begin{align*}\hat{\textbf{X}}=\textbf{X}\cup\{\Delta\}\quad\hbox{and}\quad \hat{\textbf{A}}=\textbf{A}\cup\{a_{\Delta}\},\end{align*}
\begin{align*}\hat{\textbf{X}}=\textbf{X}\cup\{\Delta\}\quad\hbox{and}\quad \hat{\textbf{A}}=\textbf{A}\cup\{a_{\Delta}\},\end{align*}
 $\hat{\textbf{X}}$
and
$\hat{\textbf{X}}$
and
 $\hat{\textbf{A}}$
are again Borel spaces.
$\hat{\textbf{A}}$
are again Borel spaces.
-
The set of available actions when the state variable is
 $x\in\hat{\textbf{X}}$
is the set
$x\in\hat{\textbf{X}}$
is the set
 $\hat{\textbf{A}}(x)\subseteq\hat{\textbf{A}}$
, where Let
$\hat{\textbf{A}}(x)\subseteq\hat{\textbf{A}}$
, where Let \begin{align*}\hat{\textbf{A}}(x)=\textbf{A}(x)\ \ \hbox{for $x\in\textbf{X}$}\quad\hbox{and}\quad\hat{\textbf{A}}(\Delta)=\{a_{\Delta}\}.\end{align*}
\begin{align*}\hat{\textbf{A}}(x)=\textbf{A}(x)\ \ \hbox{for $x\in\textbf{X}$}\quad\hbox{and}\quad\hat{\textbf{A}}(\Delta)=\{a_{\Delta}\}.\end{align*}
 $\hat{\textbf{K}}\subseteq\hat{\textbf{X}}\times\hat{\textbf{A}}$
be the set of feasible state–action pairs; hence
$\hat{\textbf{K}}\subseteq\hat{\textbf{X}}\times\hat{\textbf{A}}$
be the set of feasible state–action pairs; hence
 $\hat{\textbf{K}}=\textbf{K}\cup\{(\Delta,a_{\Delta})\}$
.
$\hat{\textbf{K}}=\textbf{K}\cup\{(\Delta,a_{\Delta})\}$
.
-
The dynamics of this model is governed by the stochastic kernel
 $Q_{\beta}$
defined by for any
$Q_{\beta}$
defined by for any \begin{align*}Q_{\beta}(\Gamma | x,a)=\ & \textbf{I}_{G}(x) \big[ \beta Q(\Gamma\cap\textbf{X} | x,a) + (1-\beta)\delta_{\Delta}(\Gamma) \big] \\ &+ \textbf{I}_{\textbf{X}-G}(x) Q(\Gamma\cap\textbf{X} | x,a) + \textbf{I}_{\{\Delta\}}(x) \delta_{\Delta}(\Gamma)\end{align*}
\begin{align*}Q_{\beta}(\Gamma | x,a)=\ & \textbf{I}_{G}(x) \big[ \beta Q(\Gamma\cap\textbf{X} | x,a) + (1-\beta)\delta_{\Delta}(\Gamma) \big] \\ &+ \textbf{I}_{\textbf{X}-G}(x) Q(\Gamma\cap\textbf{X} | x,a) + \textbf{I}_{\{\Delta\}}(x) \delta_{\Delta}(\Gamma)\end{align*}
 $\Gamma\in \boldsymbol{\mathfrak{B}}(\hat{\textbf{X}})$
and
$\Gamma\in \boldsymbol{\mathfrak{B}}(\hat{\textbf{X}})$
and
 $(x,a)\in\hat{\textbf{K}}$
.
$(x,a)\in\hat{\textbf{K}}$
.
The initial probability distribution is the same as for
 $\mathcal{M}$
, that is,
$\mathcal{M}$
, that is,
 $\nu\in\boldsymbol{\mathcal{P}}(\textbf{X})$
. With a slight abuse of notation, we will also denote by
$\nu\in\boldsymbol{\mathcal{P}}(\textbf{X})$
. With a slight abuse of notation, we will also denote by
 $\nu$
the measure
$\nu$
the measure
 $\nu(\cdot\cap\textbf{X})$
on
$\nu(\cdot\cap\textbf{X})$
on
 $\hat{\textbf{X}}$
.
$\hat{\textbf{X}}$
. -
The reward function is
 $\textbf{I}_{G}(x)$
for
$\textbf{I}_{G}(x)$
for
 $(x,a)\in\hat{\textbf{K}}$
, where
$(x,a)\in\hat{\textbf{K}}$
, where
 $G\subseteq\textbf{X}$
is the measurable set given in the definition of
$G\subseteq\textbf{X}$
is the measurable set given in the definition of
 $\mathcal{M}$
.
$\mathcal{M}$
.
Hence, the model
![]() $\mathcal{M}_{\beta}$
is indeed a standard total-expected-reward MDP parametrized by
$\mathcal{M}_{\beta}$
is indeed a standard total-expected-reward MDP parametrized by
![]() $0<\beta< 1$
. The transitions generated by
$0<\beta< 1$
. The transitions generated by
![]() $Q_{\beta}$
can be interpreted very simply as follows. If the state process is in
$Q_{\beta}$
can be interpreted very simply as follows. If the state process is in
![]() $\textbf{X}-G$
, then the transition is made according to Q, the stochastic kernel of the original model. If the state process is in G, then either the transition is made according to the original model
$\textbf{X}-G$
, then the transition is made according to Q, the stochastic kernel of the original model. If the state process is in G, then either the transition is made according to the original model
![]() $\mathcal{M}$
(with probability
$\mathcal{M}$
(with probability
![]() $\beta$
), or the state process moves to
$\beta$
), or the state process moves to
![]() $\Delta$
(with probability
$\Delta$
(with probability
![]() $1-\beta$
). Finally, it is easy to see that
$1-\beta$
). Finally, it is easy to see that
![]() $\Delta$
is an absorbing state under
$\Delta$
is an absorbing state under
![]() $a_{\Delta}$
, the unique action available at
$a_{\Delta}$
, the unique action available at
![]() $\Delta$
. However, it should be observed that
$\Delta$
. However, it should be observed that
![]() $\mathcal{M}_{\beta}$
is not necessarily an absorbing MDP in the terminology of [Reference Feinberg and Rothblum17, Section 2], because absorption in
$\mathcal{M}_{\beta}$
is not necessarily an absorbing MDP in the terminology of [Reference Feinberg and Rothblum17, Section 2], because absorption in
![]() $\Delta$
may not occur in a finite expected time.
$\Delta$
may not occur in a finite expected time.
The definition of
![]() $\mathcal{M}_{\beta}$
is somewhat inspired by the well-known equivalent formulation of a discounted MDP, with discount factor
$\mathcal{M}_{\beta}$
is somewhat inspired by the well-known equivalent formulation of a discounted MDP, with discount factor
![]() $\beta$
, as a total-reward MDP in which the transition probabilities are multiplied by the discount factor
$\beta$
, as a total-reward MDP in which the transition probabilities are multiplied by the discount factor
![]() $\beta$
, while
$\beta$
, while
![]() $1-\beta$
is the probability of killing the process at each transition; see, e.g., [Reference Feinberg and Rothblum17, p. 132]. In our case, however, the
$1-\beta$
is the probability of killing the process at each transition; see, e.g., [Reference Feinberg and Rothblum17, p. 132]. In our case, however, the
![]() $\beta$
factor is incorporated only when the process is in G.
$\beta$
factor is incorporated only when the process is in G.
Control policies. The construction and definition of the control policies for
![]() $\mathcal{M}_{\beta}$
is very similar to what was presented for the original model in Section 2. Therefore, we will just present the key elements and will skip some details. Letting
$\mathcal{M}_{\beta}$
is very similar to what was presented for the original model in Section 2. Therefore, we will just present the key elements and will skip some details. Letting
![]() $\hat{\textbf{H}}_0=\hat{\textbf{X}}$
, for
$\hat{\textbf{H}}_0=\hat{\textbf{X}}$
, for
![]() $n\ge1$
we have
$n\ge1$
we have
 \begin{align*}\hat{\textbf{H}}_n=\textbf{H}_n\cup\bigcup_{j=0}^n\big( \textbf{K}^{j}\times \{ (\Delta,a_{\Delta})\}^{n-j}\times\{\Delta\}\big),\end{align*}
\begin{align*}\hat{\textbf{H}}_n=\textbf{H}_n\cup\bigcup_{j=0}^n\big( \textbf{K}^{j}\times \{ (\Delta,a_{\Delta})\}^{n-j}\times\{\Delta\}\big),\end{align*}
which includes the histories of the original control model, plus those paths reaching
![]() $\Delta$
at time
$\Delta$
at time
![]() $0\le j\le n$
and remaining in
$0\le j\le n$
and remaining in
![]() $\Delta$
thereafter. The set of all admissible histories is given by
$\Delta$
thereafter. The set of all admissible histories is given by
The family of control policies for
![]() $\mathcal{M}_{\beta}$
is denoted by
$\mathcal{M}_{\beta}$
is denoted by
![]() $\hat{\boldsymbol{\Pi}}$
, and the family of stationary Markov policies is
$\hat{\boldsymbol{\Pi}}$
, and the family of stationary Markov policies is
![]() $\hat{\boldsymbol{\Pi}}_{s}$
. These are defined similarly to those of
$\hat{\boldsymbol{\Pi}}_{s}$
. These are defined similarly to those of
![]() $\mathcal{M}$
, where we replace
$\mathcal{M}$
, where we replace
![]() $\textbf{X}$
,
$\textbf{X}$
,
![]() $\textbf{A}$
, and
$\textbf{A}$
, and
![]() $\textbf{H}_{n}$
with
$\textbf{H}_{n}$
with
![]() $\hat{\textbf{X}}$
,
$\hat{\textbf{X}}$
,
![]() $\hat{\textbf{A}}$
, and
$\hat{\textbf{A}}$
, and
![]() $\hat{\textbf{H}}_{n}$
, respectively.
$\hat{\textbf{H}}_{n}$
, respectively.
Dynamics of the control model. Let
![]() $\hat{\boldsymbol{\Omega}}=(\hat{\textbf{X}}\times\hat{\textbf{A}})^\infty$
be the state–action canonical sample space endowed with its product
$\hat{\boldsymbol{\Omega}}=(\hat{\textbf{X}}\times\hat{\textbf{A}})^\infty$
be the state–action canonical sample space endowed with its product
![]() $\sigma$
-algebra
$\sigma$
-algebra
![]() $\hat{\boldsymbol{\mathcal{F}}}$
. The state, action, and history process projections are denoted by
$\hat{\boldsymbol{\mathcal{F}}}$
. The state, action, and history process projections are denoted by
![]() $\hat{X}_n$
,
$\hat{X}_n$
,
![]() $\hat{A}_n$
, and
$\hat{A}_n$
, and
![]() $\hat{H}_n$
, and they are defined as in Section 2. The counting processes associated to the visits of the state process to the set G are
$\hat{H}_n$
, and they are defined as in Section 2. The counting processes associated to the visits of the state process to the set G are
![]() $\hat{N}_G=\sum_{n=0}^\infty \textbf{I}_{G}(\hat{X}_n)$
and
$\hat{N}_G=\sum_{n=0}^\infty \textbf{I}_{G}(\hat{X}_n)$
and
![]() $\hat{N}_G(I)=\sum_{n\in I} \textbf{I}_{G}(\hat{X}_k)$
for
$\hat{N}_G(I)=\sum_{n\in I} \textbf{I}_{G}(\hat{X}_k)$
for
![]() $I\subseteq\mathbb{N}$
.
$I\subseteq\mathbb{N}$
.
Recall that we were considering a reference probability measure
![]() $\lambda\in\boldsymbol{\mathcal{P}}(\textbf{X})$
for the control model
$\lambda\in\boldsymbol{\mathcal{P}}(\textbf{X})$
for the control model
![]() $\mathcal{M}$
. For the auxiliary control model, we will use the reference probability measure
$\mathcal{M}$
. For the auxiliary control model, we will use the reference probability measure
![]() $\hat\lambda\in\boldsymbol{\mathcal{P}}(\hat{\textbf{X}})$
defined by
$\hat\lambda\in\boldsymbol{\mathcal{P}}(\hat{\textbf{X}})$
defined by
Given
![]() $\hat{\pi}\in\hat{\boldsymbol{\Pi}}$
and the initial distribution
$\hat{\pi}\in\hat{\boldsymbol{\Pi}}$
and the initial distribution
![]() $\nu$
, there exists a unique probability measure
$\nu$
, there exists a unique probability measure
![]() $\mathbb{P}^{\beta,\hat{\pi}}_{\nu}$
on
$\mathbb{P}^{\beta,\hat{\pi}}_{\nu}$
on
![]() $(\hat{\boldsymbol{\Omega}},\hat{\boldsymbol{\mathcal{F}}})$
supported on the set (3.1) of histories that models the dynamics of
$(\hat{\boldsymbol{\Omega}},\hat{\boldsymbol{\mathcal{F}}})$
supported on the set (3.1) of histories that models the dynamics of
![]() $\mathcal{M}_{\beta}$
. The corresponding expectation operator is denoted by
$\mathcal{M}_{\beta}$
. The corresponding expectation operator is denoted by
![]() $ \mathbb{E}^{\beta,\hat{\pi}}_{\nu}$
.
$ \mathbb{E}^{\beta,\hat{\pi}}_{\nu}$
.
Optimality criterion. For the model
![]() $\mathcal{M}_{\beta}$
, the objective is the maximization of the total-expected-reward criterion given by the expected number of visits to the set G: for any
$\mathcal{M}_{\beta}$
, the objective is the maximization of the total-expected-reward criterion given by the expected number of visits to the set G: for any
![]() $\hat{\pi}\in\hat{\boldsymbol{\Pi}}$
,
$\hat{\pi}\in\hat{\boldsymbol{\Pi}}$
,
and we let
be the value function. A policy
![]() $\pi^*\in\hat{\boldsymbol{\Pi}}$
satisfying
$\pi^*\in\hat{\boldsymbol{\Pi}}$
satisfying
![]() $\mathbb{E}^{\beta,\pi^{*}}_{\nu} [\hat{N}_G]=V^*_{\beta}(\nu)$
is said to be optimal.
$\mathbb{E}^{\beta,\pi^{*}}_{\nu} [\hat{N}_G]=V^*_{\beta}(\nu)$
is said to be optimal.
Remark 3.1. Given
![]() $\pi=\{\pi_n\}_{n\in\mathbb{N}}$
in
$\pi=\{\pi_n\}_{n\in\mathbb{N}}$
in
![]() $\boldsymbol{\Pi}$
, we can define
$\boldsymbol{\Pi}$
, we can define
![]() $\pi^{\Delta}=\{\pi^{\Delta}_n\}_{n\in\mathbb{N}}$
in
$\pi^{\Delta}=\{\pi^{\Delta}_n\}_{n\in\mathbb{N}}$
in
![]() $\hat{\boldsymbol{\Pi}}$
by setting
$\hat{\boldsymbol{\Pi}}$
by setting
![]() $\pi^{\Delta}_n(\cdot|h_n)=\pi_n(\cdot|h_n)$
whenever
$\pi^{\Delta}_n(\cdot|h_n)=\pi_n(\cdot|h_n)$
whenever
![]() $h_n\in\textbf{H}_n$
and
$h_n\in\textbf{H}_n$
and
![]() $\pi^{\Delta}_n(\cdot|h_n)=\delta_{a_{\Delta}}(\cdot)$
for
$\pi^{\Delta}_n(\cdot|h_n)=\delta_{a_{\Delta}}(\cdot)$
for
![]() $h_n=(x_0,a_0,\ldots,\Delta)\in\hat{\textbf{H}}_n-\textbf{H}_n$
. Conversely, given a control policy
$h_n=(x_0,a_0,\ldots,\Delta)\in\hat{\textbf{H}}_n-\textbf{H}_n$
. Conversely, given a control policy
![]() $\hat{\pi}=\{\hat{\pi}_n\}_{n\in\mathbb{N}}$
in
$\hat{\pi}=\{\hat{\pi}_n\}_{n\in\mathbb{N}}$
in
![]() $\hat{\boldsymbol{\Pi}}$
, we can restrict it to the sample paths in
$\hat{\boldsymbol{\Pi}}$
, we can restrict it to the sample paths in
![]() $\textbf{H}_n$
to define a control policy
$\textbf{H}_n$
to define a control policy
![]() $\hat{\pi}^{|\textbf{X}}=\{\hat{\pi}^{|\textbf{X}}_n\}_{n\in\mathbb{N}}$
in
$\hat{\pi}^{|\textbf{X}}=\{\hat{\pi}^{|\textbf{X}}_n\}_{n\in\mathbb{N}}$
in
![]() ${\boldsymbol{\Pi}}$
given by
${\boldsymbol{\Pi}}$
given by
![]() $\hat{\pi}^{|\textbf{X}}(\cdot|h_n)=\hat\pi_n(\cdot|h_n)$
when
$\hat{\pi}^{|\textbf{X}}(\cdot|h_n)=\hat\pi_n(\cdot|h_n)$
when
![]() $h_n\in\textbf{H}_n$
.
$h_n\in\textbf{H}_n$
.
Hence, there is a bijection between
![]() $\hat{\boldsymbol{\Pi}}$
and
$\hat{\boldsymbol{\Pi}}$
and
![]() $\boldsymbol{\Pi}$
. Note that this establishes a bijection between
$\boldsymbol{\Pi}$
. Note that this establishes a bijection between
![]() $\boldsymbol{\Pi}_s$
and
$\boldsymbol{\Pi}_s$
and
![]() $\hat{\boldsymbol{\Pi}}_{s}$
as well.
$\hat{\boldsymbol{\Pi}}_{s}$
as well.
For a complete overview of techniques for solving total-expected-reward MDPs, we refer to [Reference Hernández-Lerma and Lasserre19, Chapter 9]. In that reference, the value iteration algorithm, the policy iteration algorithm, and the linear programming approach are discussed. Other related results on value iteration are described in Theorems 3.5 and 3.7 in [Reference Dufour and Prieto-Rumeau15], and the linear programming (or convex analytic) approach is also studied in [Reference Dufour, Horiguchi and Piunovskiy13, Reference Dufour and Piunovskiy14].
The relation between
![]() $\mathcal{M}$
and
$\mathcal{M}$
and
![]() $\mathcal{M}_{\beta}$
. Next we state a result that allows us to establish a correspondence between the performance functions of the two models
$\mathcal{M}_{\beta}$
. Next we state a result that allows us to establish a correspondence between the performance functions of the two models
![]() $\mathcal{M}$
and
$\mathcal{M}$
and
![]() $\mathcal{M}_{\beta}$
. Roughly, this will imply that for any pair of control policies on correspondence (recall Remark 3.1), the performance criterion of the model
$\mathcal{M}_{\beta}$
. Roughly, this will imply that for any pair of control policies on correspondence (recall Remark 3.1), the performance criterion of the model
![]() $\mathcal{M}_{\beta}$
multiplied by
$\mathcal{M}_{\beta}$
multiplied by
![]() $1-\beta$
will converge, as the parameter
$1-\beta$
will converge, as the parameter
![]() $\beta$
tends towards 1, to the performance criterion of the original model
$\beta$
tends towards 1, to the performance criterion of the original model
![]() $\mathcal{M}$
. This very important fact establishes the link from
$\mathcal{M}$
. This very important fact establishes the link from
![]() $\mathcal{M}$
to a criterion of an additive nature, for which it will be possible to use standard methods of analysis. In our paper, we use the so-called direct approach, along the lines developed in [Reference Balder3, Reference Balder5, Reference Nowak23, Reference Schäl28, Reference Schäl29]; roughly speaking, this consists in finding a suitable topology on the set of strategic probability measures to ensure that it is compact and that the reward functional is semicontinuous.
$\mathcal{M}$
to a criterion of an additive nature, for which it will be possible to use standard methods of analysis. In our paper, we use the so-called direct approach, along the lines developed in [Reference Balder3, Reference Balder5, Reference Nowak23, Reference Schäl28, Reference Schäl29]; roughly speaking, this consists in finding a suitable topology on the set of strategic probability measures to ensure that it is compact and that the reward functional is semicontinuous.
The next result is proved in [Reference Dufour and Prieto-Rumeau15] in the context of a countable state space. It can easily be generalized to the framework of our paper, namely, a general state space of Borel type. In order to avoid unnecessary repetition we will omit the proof here; we refer the reader to Section 3 of [Reference Dufour and Prieto-Rumeau15]. In the sequel we make the convention that
![]() $\beta^\infty=0$
for
$\beta^\infty=0$
for
![]() $\beta\in(0, 1)$
.
$\beta\in(0, 1)$
.
Proposition 3.1. For every
![]() $0<\beta<1$
,
$0<\beta<1$
,
![]() $\pi\in\boldsymbol{\Pi}$
, and
$\pi\in\boldsymbol{\Pi}$
, and
![]() $n\in\mathbb{N}$
we have
$n\in\mathbb{N}$
we have
Remark 3.2.
-
(a) Since
 $\hat{\boldsymbol{\Pi}}=\big\{ \pi^{\Delta} \,:\, \pi\in\boldsymbol{\Pi}\big\}$
, for every
$\hat{\boldsymbol{\Pi}}=\big\{ \pi^{\Delta} \,:\, \pi\in\boldsymbol{\Pi}\big\}$
, for every
 $0<\beta<1$
,
$0<\beta<1$
,
 $\hat{\pi}\in\hat{\boldsymbol{\Pi}}$
, and
$\hat{\pi}\in\hat{\boldsymbol{\Pi}}$
, and
 $n\in\mathbb{N}$
we have and
$n\in\mathbb{N}$
we have and \begin{align*}\mathbb{E}^{\beta,\hat{\pi}}_{\nu} [\hat{N}_G([0,n])]=\frac{1}{1-\beta}\cdot \mathbb{E}^{\hat{\pi}^{|\textbf{X}}}_{\nu} [1-\beta^{N_G([0,n])}]\end{align*}
\begin{align*}\mathbb{E}^{\beta,\hat{\pi}}_{\nu} [\hat{N}_G([0,n])]=\frac{1}{1-\beta}\cdot \mathbb{E}^{\hat{\pi}^{|\textbf{X}}}_{\nu} [1-\beta^{N_G([0,n])}]\end{align*}
 \begin{align*}\mathbb{E}^{\beta,\hat{\pi}}_{\nu} [\hat{N}_G]=\frac{1}{1-\beta}\cdot \mathbb{E}^{\hat{\pi}^{|\textbf{X}}}_{\nu} [1-\beta^{N_G}].\end{align*}
\begin{align*}\mathbb{E}^{\beta,\hat{\pi}}_{\nu} [\hat{N}_G]=\frac{1}{1-\beta}\cdot \mathbb{E}^{\hat{\pi}^{|\textbf{X}}}_{\nu} [1-\beta^{N_G}].\end{align*}
-
(b) Since
 $1-\beta^{N_G}$
decreases to
$1-\beta^{N_G}$
decreases to
 $\textbf{I}_{\{N_{G}=\infty\}}$
as
$\textbf{I}_{\{N_{G}=\infty\}}$
as
 $\beta$
increases to 1, by dominated convergence we have for any
$\beta$
increases to 1, by dominated convergence we have for any
 $\pi\in\boldsymbol{\Pi}$
So the performance criterion of
$\pi\in\boldsymbol{\Pi}$
So the performance criterion of \begin{align*}\lim_{\beta\uparrow1} (1-\beta) \mathbb{E}^{\beta,\pi^{\Delta}}_{\nu} [\hat{N}_G]=\lim_{\beta\uparrow1} \mathbb{E}^{\pi}_{\nu}[1-\beta^{N_G}]=\mathbb{P}^{\pi}_{\nu}\{N_{G}=\infty\}.\end{align*}
\begin{align*}\lim_{\beta\uparrow1} (1-\beta) \mathbb{E}^{\beta,\pi^{\Delta}}_{\nu} [\hat{N}_G]=\lim_{\beta\uparrow1} \mathbb{E}^{\pi}_{\nu}[1-\beta^{N_G}]=\mathbb{P}^{\pi}_{\nu}\{N_{G}=\infty\}.\end{align*}
 $\mathcal{M}_{\beta}$
multiplied by
$\mathcal{M}_{\beta}$
multiplied by
 $1-\beta$
converges as
$1-\beta$
converges as
 $\beta\uparrow1$
to that of
$\beta\uparrow1$
to that of
 $\mathcal{M}$
for each single control policy.
$\mathcal{M}$
for each single control policy.
Assumptions on
![]() $\mathcal{M}_{\beta}$
. We define the time of entrance of the state process
$\mathcal{M}_{\beta}$
. We define the time of entrance of the state process
![]() $\{\hat{X}_n\}_{n\in\mathbb{N}}$
into a subset
$\{\hat{X}_n\}_{n\in\mathbb{N}}$
into a subset
![]() $\mathcal{C}\in\boldsymbol{\mathfrak{B}}(\hat{\textbf{X}})$
of the state space as the random variable
$\mathcal{C}\in\boldsymbol{\mathfrak{B}}(\hat{\textbf{X}})$
of the state space as the random variable
![]() $\tau_{\mathcal{C}}$
defined on
$\tau_{\mathcal{C}}$
defined on
![]() $\hat{\boldsymbol{\Omega}}$
by
$\hat{\boldsymbol{\Omega}}$
by
with the usual convention that the minimum over the empty set is
![]() $\infty$
.
$\infty$
.
For a stationary Markov policy
![]() $\pi\in\boldsymbol{\Pi}_s$
, we define the stochastic kernel
$\pi\in\boldsymbol{\Pi}_s$
, we define the stochastic kernel
![]() $Q_{\pi}$
on
$Q_{\pi}$
on
![]() $\textbf{X}$
given
$\textbf{X}$
given
![]() $\textbf{X}$
as
$\textbf{X}$
as
For
![]() $n\ge1$
, we denote by
$n\ge1$
, we denote by
![]() $Q^n_{\pi}$
the nth composition of
$Q^n_{\pi}$
the nth composition of
![]() $Q_{\pi}$
with itself, and we make the convention that
$Q_{\pi}$
with itself, and we make the convention that
![]() $Q^0_{\pi}(\cdot|x)=\delta_x(\cdot)$
. Similarly, for a stationary Markov policy
$Q^0_{\pi}(\cdot|x)=\delta_x(\cdot)$
. Similarly, for a stationary Markov policy
![]() $\hat{\pi}\in\hat{\boldsymbol{\Pi}}_s$
of the auxiliary control model, we define the stochastic kernel
$\hat{\pi}\in\hat{\boldsymbol{\Pi}}_s$
of the auxiliary control model, we define the stochastic kernel
![]() $Q_{\beta,\hat{\pi}}$
on
$Q_{\beta,\hat{\pi}}$
on
![]() $\hat{\textbf{X}}$
given
$\hat{\textbf{X}}$
given
![]() $\hat{\textbf{X}}$
and
$\hat{\textbf{X}}$
and
![]() $Q^n_{\beta,\hat{\pi}}$
for
$Q^n_{\beta,\hat{\pi}}$
for
![]() $n\ge0$
.
$n\ge0$
.
Assumption B. For each
![]() $0<\beta<1$
and
$0<\beta<1$
and
![]() $\hat{\pi}\in\hat{\boldsymbol{\Pi}}_{s}$
, there exists a measurable set
$\hat{\pi}\in\hat{\boldsymbol{\Pi}}_{s}$
, there exists a measurable set
![]() $\mathcal{C}^{\beta,\hat{\pi}}\subseteq \hat{\textbf{X}}$
satisfying
$\mathcal{C}^{\beta,\hat{\pi}}\subseteq \hat{\textbf{X}}$
satisfying
![]() $\hat{\lambda}(G\cap \mathcal{C}^{\beta,\hat{\pi}})=0$
and
$\hat{\lambda}(G\cap \mathcal{C}^{\beta,\hat{\pi}})=0$
and
![]() $Q_{\beta,\hat{\pi}}(\mathcal{C}^{\beta,\hat{\pi}} |x)=1$
for
$Q_{\beta,\hat{\pi}}(\mathcal{C}^{\beta,\hat{\pi}} |x)=1$
for
![]() $\hat{\lambda}$
-almost all
$\hat{\lambda}$
-almost all
![]() $x\in\mathcal{C}^{\beta,\hat{\pi}}$
. In addition, there exists a finite constant
$x\in\mathcal{C}^{\beta,\hat{\pi}}$
. In addition, there exists a finite constant
![]() $K_{\beta}$
such that for every
$K_{\beta}$
such that for every
![]() $\hat\pi\in\hat{\boldsymbol{\Pi}}_s$
,
$\hat\pi\in\hat{\boldsymbol{\Pi}}_s$
,
Observe that, under Assumption B, the control model
![]() $\mathcal{M}_{\beta}$
is not necessarily an absorbing MDP in the terminology of [Reference Feinberg and Rothblum17, Section 2], since the set
$\mathcal{M}_{\beta}$
is not necessarily an absorbing MDP in the terminology of [Reference Feinberg and Rothblum17, Section 2], since the set
![]() $\mathcal{C}^{\beta,\hat{\pi}}$
depends on the control policy. The stability Assumption B can be informally and very loosely explained as follows. Given any fixed
$\mathcal{C}^{\beta,\hat{\pi}}$
depends on the control policy. The stability Assumption B can be informally and very loosely explained as follows. Given any fixed
![]() $0<\beta<1$
, for each stationary Markov policy
$0<\beta<1$
, for each stationary Markov policy
![]() $\hat\pi\in\hat{\boldsymbol{\Pi}}_s$
there exists a set
$\hat\pi\in\hat{\boldsymbol{\Pi}}_s$
there exists a set
![]() $\mathcal{C}^{\beta,\hat{\pi}}$
which is closed (not in the topological sense, but in the terminology of Markov chains) and disjoint from G, and which is reached in a bounded expected time when starting from outside it (formally, all these statements hold almost surely with respect to the reference measure
$\mathcal{C}^{\beta,\hat{\pi}}$
which is closed (not in the topological sense, but in the terminology of Markov chains) and disjoint from G, and which is reached in a bounded expected time when starting from outside it (formally, all these statements hold almost surely with respect to the reference measure
![]() $\hat\lambda$
).
$\hat\lambda$
).
We now state some consequences of Assumption B.
Lemma 3.1. Let Assumption B be satisfied. Then for any
![]() $x\in\hat{\textbf{X}}$
,
$x\in\hat{\textbf{X}}$
,
![]() $\hat{\pi}\in\hat{\boldsymbol{\Pi}}_{s}$
, and
$\hat{\pi}\in\hat{\boldsymbol{\Pi}}_{s}$
, and
![]() $n\ge1$
we have
$n\ge1$
we have
![]() $Q^n_{\beta,\hat{\pi}}(\cdot|x)\ll \hat{\lambda}$
. In particular, the distribution of
$Q^n_{\beta,\hat{\pi}}(\cdot|x)\ll \hat{\lambda}$
. In particular, the distribution of
![]() $\hat{X}_{n}$
under
$\hat{X}_{n}$
under
![]() $\mathbb{P}^{\beta,\hat{\pi}}_{\nu}$
is absolutely continuous with respect to
$\mathbb{P}^{\beta,\hat{\pi}}_{\nu}$
is absolutely continuous with respect to
![]() $\hat{\lambda}$
for any
$\hat{\lambda}$
for any
![]() $n\in\mathbb{N}$
.
$n\in\mathbb{N}$
.
Proof. Indeed, if
![]() $\Gamma\in\boldsymbol{\mathfrak{B}}(\hat{\textbf{X}})$
is such that
$\Gamma\in\boldsymbol{\mathfrak{B}}(\hat{\textbf{X}})$
is such that
![]() $\hat\lambda(\Gamma)=0$
, then necessarily
$\hat\lambda(\Gamma)=0$
, then necessarily
![]() $\Gamma\subseteq\textbf{X}$
with
$\Gamma\subseteq\textbf{X}$
with
![]() $\lambda(\Gamma)=0$
. By definition of the stochastic kernel
$\lambda(\Gamma)=0$
. By definition of the stochastic kernel
![]() $Q_{\beta}$
, and recalling (2.1), it is then clear that
$Q_{\beta}$
, and recalling (2.1), it is then clear that
![]() $Q_{\beta,\hat\pi}(\Gamma|x)=0$
for every
$Q_{\beta,\hat\pi}(\Gamma|x)=0$
for every
![]() $x\in\hat{\textbf{X}}$
. Now, supposing again that
$x\in\hat{\textbf{X}}$
. Now, supposing again that
![]() $\Gamma\in\boldsymbol{\mathfrak{B}}(\hat{\textbf{X}})$
is such that
$\Gamma\in\boldsymbol{\mathfrak{B}}(\hat{\textbf{X}})$
is such that
![]() $\hat\lambda(\Gamma)=0$
, and letting
$\hat\lambda(\Gamma)=0$
, and letting
![]() $n\ge1$
and
$n\ge1$
and
![]() $x\in\textbf{X}$
, we have
$x\in\textbf{X}$
, we have
which indeed equals 0 because
![]() $Q_{\beta,\hat\pi}(\Gamma|y)=0$
.
$Q_{\beta,\hat\pi}(\Gamma|y)=0$
.
The second statement is a straightforward consequence of the above results except for the case
![]() $n=0$
. In that case, however, the distribution of
$n=0$
. In that case, however, the distribution of
![]() $\hat{X}_0$
is
$\hat{X}_0$
is
![]() $\nu\ll\lambda$
.
$\nu\ll\lambda$
.
The fact that
![]() $\mathcal{C}^{\beta,\hat\pi}$
is closed
$\mathcal{C}^{\beta,\hat\pi}$
is closed
![]() $\hat\lambda$
-almost surely under
$\hat\lambda$
-almost surely under
![]() $\hat\pi$
is extended to further transitions.
$\hat\pi$
is extended to further transitions.
Lemma 3.2. Suppose that Assumption B holds. Given arbitrary
![]() $\hat{\pi}\in\hat{\boldsymbol{\Pi}}_{s}$
and
$\hat{\pi}\in\hat{\boldsymbol{\Pi}}_{s}$
and
![]() $n\ge1$
, we have that
$n\ge1$
, we have that
![]() $Q^{n}_{\beta,\hat{\pi}}(\mathcal{C}^{\beta,\hat{\pi}}|x)=1$
for
$Q^{n}_{\beta,\hat{\pi}}(\mathcal{C}^{\beta,\hat{\pi}}|x)=1$
for
![]() $\hat{\lambda}$
-almost all
$\hat{\lambda}$
-almost all
![]() $x\in\mathcal{C}^{\beta,\hat{\pi}}$
.
$x\in\mathcal{C}^{\beta,\hat{\pi}}$
.
Proof. Let us prove the result by induction. By Assumption B, it holds for
![]() $n=1$
. Now assume that the claim holds for some
$n=1$
. Now assume that the claim holds for some
![]() $n\ge1$
. Let
$n\ge1$
. Let
![]() $C_n\subseteq \mathcal{C}^{\beta,\hat\pi}$
, with
$C_n\subseteq \mathcal{C}^{\beta,\hat\pi}$
, with
![]() $\hat\lambda(\mathcal{C}^{\beta,\hat\pi}-C_n)=0$
, be the set of
$\hat\lambda(\mathcal{C}^{\beta,\hat\pi}-C_n)=0$
, be the set of
![]() $x\in\hat{\textbf{X}}$
for which
$x\in\hat{\textbf{X}}$
for which
![]() $Q_{\beta,\hat\pi}(\mathcal{C}^{\beta,\hat\pi}|x)=1$
and
$Q_{\beta,\hat\pi}(\mathcal{C}^{\beta,\hat\pi}|x)=1$
and
![]() $Q^n_{\beta,\hat\pi}(\mathcal{C}^{\beta,\hat\pi}|x)=1$
. If
$Q^n_{\beta,\hat\pi}(\mathcal{C}^{\beta,\hat\pi}|x)=1$
. If
![]() $x\in C_n$
we have
$x\in C_n$
we have
Since
![]() $Q_{\beta,\hat\pi}(\cdot|x)\ll \hat\lambda$
(recall Lemma 3.1), it follows that
$Q_{\beta,\hat\pi}(\cdot|x)\ll \hat\lambda$
(recall Lemma 3.1), it follows that
giving the result.
We conclude this section by proposing a sufficient condition for Assumption B. It imposes a drift towards a closed set with
![]() $\hat\lambda$
-null intersection with G by using some standard Foster–Lyapunov criteria. Such conditions are well known in the field of Markov chains. They provide easily verifiable conditions for testing stability (existence of invariant measure, recurrence, ergodicity, etc.).
$\hat\lambda$
-null intersection with G by using some standard Foster–Lyapunov criteria. Such conditions are well known in the field of Markov chains. They provide easily verifiable conditions for testing stability (existence of invariant measure, recurrence, ergodicity, etc.).
Proposition 3.2. Suppose that for each
![]() $0<\beta<1$
and
$0<\beta<1$
and
![]() $\hat{\pi}\in\hat{\boldsymbol{\Pi}}_{s}$
there exist a constant
$\hat{\pi}\in\hat{\boldsymbol{\Pi}}_{s}$
there exist a constant
![]() $\gamma^{\beta,\hat{\pi}}\ge0$
and the following:
$\gamma^{\beta,\hat{\pi}}\ge0$
and the following:
-
a measurable function
 $W^{\beta,\hat{\pi}}\,:\, \hat{\textbf{X}} \rightarrow [0,+\infty]$
satisfying (3.3)and such that the set
$W^{\beta,\hat{\pi}}\,:\, \hat{\textbf{X}} \rightarrow [0,+\infty]$
satisfying (3.3)and such that the set \begin{eqnarray} Q_{\beta,\hat{\pi}} W^{\beta,\hat{\pi}}(x) \leq W^{\beta,\hat{\pi}}(x)+\gamma^{\beta,\hat{\pi}} \quad for\ \hat{\lambda}-almost\ all\ x\in\hat{\textbf{X}} \end{eqnarray}
\begin{eqnarray} Q_{\beta,\hat{\pi}} W^{\beta,\hat{\pi}}(x) \leq W^{\beta,\hat{\pi}}(x)+\gamma^{\beta,\hat{\pi}} \quad for\ \hat{\lambda}-almost\ all\ x\in\hat{\textbf{X}} \end{eqnarray}
 $\mathcal{C}^{\beta,\hat{\pi}}$
defined as
$\mathcal{C}^{\beta,\hat{\pi}}$
defined as
 $\mathcal{C}^{\beta,\hat{\pi}}=\{x\in\hat{\textbf{X}}\,:\, W^{\beta,\hat{\pi}}(x) <+\infty\}$
satisfies
$\mathcal{C}^{\beta,\hat{\pi}}=\{x\in\hat{\textbf{X}}\,:\, W^{\beta,\hat{\pi}}(x) <+\infty\}$
satisfies
 $\hat{\lambda}(\mathcal{C}^{\beta,\hat{\pi}})>0$
and
$\hat{\lambda}(\mathcal{C}^{\beta,\hat{\pi}})>0$
and
 $\hat{\lambda}(G\cap \mathcal{C}^{\beta,\hat{\pi}})=0$
;
$\hat{\lambda}(G\cap \mathcal{C}^{\beta,\hat{\pi}})=0$
;
-
a measurable function
 $V^{\beta,\hat{\pi}}\,:\, \hat{\textbf{X}} \rightarrow [0,+\infty]$
and a constant
$V^{\beta,\hat{\pi}}\,:\, \hat{\textbf{X}} \rightarrow [0,+\infty]$
and a constant
 $K_{\beta}<+\infty$
satisfying (3.4)and
$K_{\beta}<+\infty$
satisfying (3.4)and \begin{eqnarray}V^{\beta,\hat{\pi}}(x) \leq K_{\beta}\quad for\ \hat{\lambda}-almost\ all\ x\in\hat{\textbf{X}}-\mathcal{C}^{\beta,\hat{\pi}} \end{eqnarray}
(3.5)
\begin{eqnarray}V^{\beta,\hat{\pi}}(x) \leq K_{\beta}\quad for\ \hat{\lambda}-almost\ all\ x\in\hat{\textbf{X}}-\mathcal{C}^{\beta,\hat{\pi}} \end{eqnarray}
(3.5) \begin{eqnarray}Q_{\beta,\hat{\pi}} V^{\beta,\hat{\pi}}(x) \leq V^{\beta,\hat{\pi}}(x)-1+ \gamma^{\beta,\hat{\pi}} \textbf{I}_{\mathcal{C}^{\beta,\hat{\pi}}}(x) \quad for\ \hat{\lambda}-almost\ all\ x\in\hat{\textbf{X}}.\end{eqnarray}
\begin{eqnarray}Q_{\beta,\hat{\pi}} V^{\beta,\hat{\pi}}(x) \leq V^{\beta,\hat{\pi}}(x)-1+ \gamma^{\beta,\hat{\pi}} \textbf{I}_{\mathcal{C}^{\beta,\hat{\pi}}}(x) \quad for\ \hat{\lambda}-almost\ all\ x\in\hat{\textbf{X}}.\end{eqnarray}
Under these conditions, Assumption B is satisfied.
Proof. Let
![]() $0<\beta<1$
and
$0<\beta<1$
and
![]() $\hat{\pi}\in\hat{\boldsymbol{\Pi}}_{s}$
. The inequality (3.3) implies that
$\hat{\pi}\in\hat{\boldsymbol{\Pi}}_{s}$
. The inequality (3.3) implies that
But since
![]() $W^{\beta,\hat\pi}(y)$
is infinite when
$W^{\beta,\hat\pi}(y)$
is infinite when
![]() $y\notin\mathcal{C}^{\beta,\hat\pi}$
and
$y\notin\mathcal{C}^{\beta,\hat\pi}$
and
![]() $W^{\beta,\hat\pi}(x)$
is finite on
$W^{\beta,\hat\pi}(x)$
is finite on
![]() $\mathcal{C}^{\beta,\hat\pi}$
, this implies that
$\mathcal{C}^{\beta,\hat\pi}$
, this implies that
![]() $Q_{\beta,\hat{\pi}}(\hat{\textbf{X}}-\mathcal{C}^{\beta,\hat{\pi}}|x)=0$
and so
$Q_{\beta,\hat{\pi}}(\hat{\textbf{X}}-\mathcal{C}^{\beta,\hat{\pi}}|x)=0$
and so
![]() $Q_{\beta,\hat{\pi}}(\mathcal{C}^{\beta,\hat{\pi}}|x)=1$
for
$Q_{\beta,\hat{\pi}}(\mathcal{C}^{\beta,\hat{\pi}}|x)=1$
for
![]() $\hat{\lambda}$
-almost all
$\hat{\lambda}$
-almost all
![]() $x\in\mathcal{C}^{\beta,\hat{\pi}}$
. This establishes the first part of Assumption B. Now, following the proof of Lemma 11.3.6 in [Reference Meyn and Tweedie22] and combining (2.1) and (3.5), we get
$x\in\mathcal{C}^{\beta,\hat{\pi}}$
. This establishes the first part of Assumption B. Now, following the proof of Lemma 11.3.6 in [Reference Meyn and Tweedie22] and combining (2.1) and (3.5), we get
![]() $\mathbb{E}^{\beta,\hat{\pi}}_{x}[\tau_{\mathcal{C}^{\beta,\hat{\pi}}}] \leq V^{\beta,\hat{\pi}}(x) $
for
$\mathbb{E}^{\beta,\hat{\pi}}_{x}[\tau_{\mathcal{C}^{\beta,\hat{\pi}}}] \leq V^{\beta,\hat{\pi}}(x) $
for
![]() $\hat{\lambda}$
-almost all
$\hat{\lambda}$
-almost all
![]() $x\in\hat{\textbf{X}}-\mathcal{C}^{\beta,\hat{\pi}}$
. The stated result follows from (3.4).
$x\in\hat{\textbf{X}}-\mathcal{C}^{\beta,\hat{\pi}}$
. The stated result follows from (3.4).
We note that the sufficient conditions given in Proposition 3.2 above are, in general, more easily verifiable than Assumption B. Indeed, Proposition 3.2 involves just the one-step transitions of the system (see (3.3) and (3.5)). On the other hand, checking Assumption B directly requires one to compute the expected hitting time of the set
![]() $\mathcal{C}^{\beta,\hat\pi}$
, which in principle requires knowledge of the distribution of the Markov chain over the whole time horizon, and then check that these expected hitting times are bounded uniformly in the initial state of the system.
$\mathcal{C}^{\beta,\hat\pi}$
, which in principle requires knowledge of the distribution of the Markov chain over the whole time horizon, and then check that these expected hitting times are bounded uniformly in the initial state of the system.
It is worth mentioning that the condition (3.3) yields, loosely, the partition between recurrent and transient states of the Markov chain, while (3.5) is closely related to the computation of the expected absorption time by the set of recurrent states of the Markov chain.
Next, in Example 3.1, we illustrate the verification of the conditions in Proposition 3.2; see also Example 4.1 below.
Example 3.1. (Taken from [Reference Dufour and Prieto-Rumeau15, Example 4.6].) Consider the state space
![]() $\textbf{X}=\{0,1,2\}$
with no actions at states 0 and 2, and
$\textbf{X}=\{0,1,2\}$
with no actions at states 0 and 2, and
![]() $\textbf{A}(1)=\{a_1,a_2\}$
. The transition probabilities from state 0 are
$\textbf{A}(1)=\{a_1,a_2\}$
. The transition probabilities from state 0 are
![]() $q(0,0)=q(0,2)=1/2$
, and from state 2 they are
$q(0,0)=q(0,2)=1/2$
, and from state 2 they are
![]() $q(2,2)=1$
(we do not make any action explicit in this notation, since there are no actions at 0 and 2). The transitions from state 1 are
$q(2,2)=1$
(we do not make any action explicit in this notation, since there are no actions at 0 and 2). The transitions from state 1 are
![]() $q(1,a_1,0)=2/3$
and
$q(1,a_1,0)=2/3$
and
![]() $q(1,a_1,1)=1/3$
under
$q(1,a_1,1)=1/3$
under
![]() $a_1$
, and
$a_1$
, and
![]() $q(1,a_2,0)=q(1,a_2,1)=$
$q(1,a_2,0)=q(1,a_2,1)=$
![]() $q(1,a_2,2)=1/3$
under
$q(1,a_2,2)=1/3$
under
![]() $a_2$
. We let
$a_2$
. We let
![]() $G=\{0\}$
. We can identify
$G=\{0\}$
. We can identify
![]() $\hat{\boldsymbol{\Pi}}_s$
with the interval [0, 1], where
$\hat{\boldsymbol{\Pi}}_s$
with the interval [0, 1], where
![]() $a\in[0, 1]$
is the probability of selecting
$a\in[0, 1]$
is the probability of selecting
![]() $a_1$
and
$a_1$
and
![]() $1-a$
is the probability of choosing action
$1-a$
is the probability of choosing action
![]() $a_2$
. Let 1 be the initial state of the system.
$a_2$
. Let 1 be the initial state of the system.
In order to verify Assumption B, we will use the sufficient conditions in Proposition 3.2. After adding the cemetery state
![]() $\Delta$
, the transition matrix for the stationary policy
$\Delta$
, the transition matrix for the stationary policy
![]() $a\in[0, 1]$
in the model
$a\in[0, 1]$
in the model
![]() $\mathcal{M}_{\beta}$
is
$\mathcal{M}_{\beta}$
is
 \begin{align*}\begin{pmatrix} \beta/2 & \quad 0 & \quad \beta/2 & \quad 1-\beta \\(1+a)/3 & \quad 1/3 & \quad (1-a)/3 & \quad 0 \\0 & \quad 0 & \quad 1 & \quad 0 \\0 & \quad 0 & \quad 0 & \quad 1\end{pmatrix},\end{align*}
\begin{align*}\begin{pmatrix} \beta/2 & \quad 0 & \quad \beta/2 & \quad 1-\beta \\(1+a)/3 & \quad 1/3 & \quad (1-a)/3 & \quad 0 \\0 & \quad 0 & \quad 1 & \quad 0 \\0 & \quad 0 & \quad 0 & \quad 1\end{pmatrix},\end{align*}
where the states are ordered
![]() $0,1,2,\Delta$
.
$0,1,2,\Delta$
.
Letting
![]() $W^{\beta,a}=(+\infty,+\infty,1,1)$
and
$W^{\beta,a}=(+\infty,+\infty,1,1)$
and
![]() $\gamma^{\beta,a}=1$
, we observe that (3.3) in Proposition 3.2 holds with, therefore,
$\gamma^{\beta,a}=1$
, we observe that (3.3) in Proposition 3.2 holds with, therefore,
![]() $\mathcal{C}^{\beta,a}=\{2,\Delta\}$
(roughly, W equals 1 on the recurrent states of the Markov chain, and it is infinite on the transient states). Regarding the inequalities (3.5), we obtain their minimal nonnegative solution, which is
$\mathcal{C}^{\beta,a}=\{2,\Delta\}$
(roughly, W equals 1 on the recurrent states of the Markov chain, and it is infinite on the transient states). Regarding the inequalities (3.5), we obtain their minimal nonnegative solution, which is
This minimal nonnegative solution is precisely the expected time the Markov chain spends in the transient states.
Solving the total-expected-reward MDP model
![]() $\mathcal{M}_{\beta}$
yields the optimal policy
$\mathcal{M}_{\beta}$
yields the optimal policy
![]() $\hat\pi^*_{\beta}=1$
with
$\hat\pi^*_{\beta}=1$
with
![]() $V^*_{\beta}(1)=\frac{2}{2-\beta}+\frac{3}{2}$
for every
$V^*_{\beta}(1)=\frac{2}{2-\beta}+\frac{3}{2}$
for every
![]() $0<\beta<1$
.
$0<\beta<1$
.
4. Main results
In this section we prove our results on the solution of the control model
![]() $\mathcal{M}$
.
$\mathcal{M}$
.
Proposition 4.1. Under Assumptions A and B, for each
![]() $0<\beta<1$
the mapping
$0<\beta<1$
the mapping
is lower semicontinuous on
![]() $\boldsymbol{\mathcal{S}}_{\nu}$
and continuous on
$\boldsymbol{\mathcal{S}}_{\nu}$
and continuous on
![]() $\boldsymbol{\mathcal{S}}_{\nu}^{s}$
.
$\boldsymbol{\mathcal{S}}_{\nu}^{s}$
.
Proof. First we prove the following preliminary fact:
for any
![]() $0<\beta<1$
. Observe that for arbitrary
$0<\beta<1$
. Observe that for arbitrary
![]() $\hat{\pi}\in\hat{\boldsymbol{\Pi}}_{s}$
and
$\hat{\pi}\in\hat{\boldsymbol{\Pi}}_{s}$
and
![]() $m\geq n\ge0$
,
$m\geq n\ge0$
,
 \begin{eqnarray*}\mathbb{P}^{\beta,\hat{\pi}}_{\nu}\{\tau_{\mathcal{C}^{\beta,\hat{\pi}}}=n,\hat{X}_{m}\in G\}&\,\leq\,&\mathbb{P}^{\beta,\hat\pi}_{\nu}\{\hat{X}_{n}\in\mathcal{C}^{\beta,\hat{\pi}},\hat{X}_{m}\in G \}\\&=& \,\mathbb{E}^{\beta,\hat\pi}_{\nu}[ Q^{m-n}_{\beta,\hat{\pi}}(G|\hat{X}_{n}) \textbf{I}_{\mathcal{C}^{\beta,\hat{\pi}}}(\hat{X}_{n})].\end{eqnarray*}
\begin{eqnarray*}\mathbb{P}^{\beta,\hat{\pi}}_{\nu}\{\tau_{\mathcal{C}^{\beta,\hat{\pi}}}=n,\hat{X}_{m}\in G\}&\,\leq\,&\mathbb{P}^{\beta,\hat\pi}_{\nu}\{\hat{X}_{n}\in\mathcal{C}^{\beta,\hat{\pi}},\hat{X}_{m}\in G \}\\&=& \,\mathbb{E}^{\beta,\hat\pi}_{\nu}[ Q^{m-n}_{\beta,\hat{\pi}}(G|\hat{X}_{n}) \textbf{I}_{\mathcal{C}^{\beta,\hat{\pi}}}(\hat{X}_{n})].\end{eqnarray*}
Recalling that
![]() $\hat{\lambda}(G\cap\mathcal{C}^{\beta,\hat{\pi}})=0$
, Lemmas 3.1 and 3.2 imply that the above expectation vanishes, and so
$\hat{\lambda}(G\cap\mathcal{C}^{\beta,\hat{\pi}})=0$
, Lemmas 3.1 and 3.2 imply that the above expectation vanishes, and so
![]() $\mathbb{P}^{\beta,\hat{\pi}}_{\nu}\{\tau_{\mathcal{C}^{\beta,\hat{\pi}}}=n,\hat{X}_{m}\in G\}=0$
. Therefore, we have
$\mathbb{P}^{\beta,\hat{\pi}}_{\nu}\{\tau_{\mathcal{C}^{\beta,\hat{\pi}}}=n,\hat{X}_{m}\in G\}=0$
. Therefore, we have
 \begin{align*}\hat{N}_G([n,\infty))= \textbf{I}_{\{\tau_{\mathcal{C}^{\beta,\hat{\pi}}}>n\}} \sum_{m=n}^{\tau_{\mathcal{C}^{\beta,\hat{\pi}}}-1}\textbf{I}_{G}(\hat{X}_{m}) \le (\tau_{\mathcal{C}^{\beta,\hat{\pi}}}-n)^+ \quad \mathbb{P}^{\beta,\hat{\pi}}_{\nu}\text{-almost surely,}\end{align*}
\begin{align*}\hat{N}_G([n,\infty))= \textbf{I}_{\{\tau_{\mathcal{C}^{\beta,\hat{\pi}}}>n\}} \sum_{m=n}^{\tau_{\mathcal{C}^{\beta,\hat{\pi}}}-1}\textbf{I}_{G}(\hat{X}_{m}) \le (\tau_{\mathcal{C}^{\beta,\hat{\pi}}}-n)^+ \quad \mathbb{P}^{\beta,\hat{\pi}}_{\nu}\text{-almost surely,}\end{align*}
and so
 \begin{eqnarray*} \mathbb{E}^{\beta,\hat{\pi}}_{\nu}[\hat{N}_G([n,\infty))] &\,\le\, & \sum_{m>n}^\infty(m-n) \mathbb{P}^{\beta,\hat{\pi}}_{\nu} \{\tau_{\mathcal{C}^{\beta,\hat{\pi}}}=m\} \\&=& \, \sum_{m>n}^\infty(m-n) \mathbb{E}^{\beta,\hat{\pi}}_{\nu} \big[ \textbf{I}_{\hat{\textbf{X}}-\mathcal{C}^{\beta,\hat{\pi}}}(\hat{X}_{n}) \;\mathbb{P}^{\beta,\hat{\pi}}_{\hat{X}_{n}} \{\tau_{\mathcal{C}^{\beta,\hat{\pi}}}=m-n\} \big]\end{eqnarray*}
\begin{eqnarray*} \mathbb{E}^{\beta,\hat{\pi}}_{\nu}[\hat{N}_G([n,\infty))] &\,\le\, & \sum_{m>n}^\infty(m-n) \mathbb{P}^{\beta,\hat{\pi}}_{\nu} \{\tau_{\mathcal{C}^{\beta,\hat{\pi}}}=m\} \\&=& \, \sum_{m>n}^\infty(m-n) \mathbb{E}^{\beta,\hat{\pi}}_{\nu} \big[ \textbf{I}_{\hat{\textbf{X}}-\mathcal{C}^{\beta,\hat{\pi}}}(\hat{X}_{n}) \;\mathbb{P}^{\beta,\hat{\pi}}_{\hat{X}_{n}} \{\tau_{\mathcal{C}^{\beta,\hat{\pi}}}=m-n\} \big]\end{eqnarray*}
by the Markov property. Then it follows that
 \begin{eqnarray*} \mathbb{E}^{\beta,\hat{\pi}}_{\nu}[\hat{N}_G([n,\infty))] &\,\le\, & \mathbb{E}^{\beta,\hat{\pi}}_{\nu} \big[ \textbf{I}_{\hat{\textbf{X}}-\mathcal{C}^{\beta,\hat{\pi}}}(\hat{X}_{n}) \cdot \sum_{m>n}^\infty(m-n) \mathbb{P}^{\beta,\hat{\pi}}_{\hat{X}_{n}} \{\tau_{\mathcal{C}^{\beta,\hat{\pi}}}=m-n\} \big] \\ &=& \, \mathbb{E}^{\beta,\hat{\pi}}_{\nu} \big[ \textbf{I}_{\hat{\textbf{X}}-\mathcal{C}^{\beta,\hat{\pi}}}(\hat{X}_{n}) \cdot\mathbb{E}^{\beta,\hat{\pi}}_{\hat{X}_{n}} [\tau_{\mathcal{C}^{\beta,\hat{\pi}}} ] \big] \\ &\le&\, \mathbb{E}^{\beta,\hat{\pi}}_{\nu} \big[ \textbf{I}_{\hat{\textbf{X}}-\mathcal{C}^{\beta,\hat{\pi}}}(\hat{X}_{n}) \cdot K_{\beta}\big],\end{eqnarray*}
\begin{eqnarray*} \mathbb{E}^{\beta,\hat{\pi}}_{\nu}[\hat{N}_G([n,\infty))] &\,\le\, & \mathbb{E}^{\beta,\hat{\pi}}_{\nu} \big[ \textbf{I}_{\hat{\textbf{X}}-\mathcal{C}^{\beta,\hat{\pi}}}(\hat{X}_{n}) \cdot \sum_{m>n}^\infty(m-n) \mathbb{P}^{\beta,\hat{\pi}}_{\hat{X}_{n}} \{\tau_{\mathcal{C}^{\beta,\hat{\pi}}}=m-n\} \big] \\ &=& \, \mathbb{E}^{\beta,\hat{\pi}}_{\nu} \big[ \textbf{I}_{\hat{\textbf{X}}-\mathcal{C}^{\beta,\hat{\pi}}}(\hat{X}_{n}) \cdot\mathbb{E}^{\beta,\hat{\pi}}_{\hat{X}_{n}} [\tau_{\mathcal{C}^{\beta,\hat{\pi}}} ] \big] \\ &\le&\, \mathbb{E}^{\beta,\hat{\pi}}_{\nu} \big[ \textbf{I}_{\hat{\textbf{X}}-\mathcal{C}^{\beta,\hat{\pi}}}(\hat{X}_{n}) \cdot K_{\beta}\big],\end{eqnarray*}
where the last inequality is obtained because
![]() $\mathbb{E}^{\beta,\hat{\pi}}_{x} [\tau_{\mathcal{C}^{\beta,\hat{\pi}}} ]\le K_{\beta}$
for
$\mathbb{E}^{\beta,\hat{\pi}}_{x} [\tau_{\mathcal{C}^{\beta,\hat{\pi}}} ]\le K_{\beta}$
for
![]() $\hat\lambda$
-almost every
$\hat\lambda$
-almost every
![]() $x\in\hat{\textbf{X}}-\mathcal{C}^{\beta,\hat\pi}$
—recall (3.2)—and because the distribution of
$x\in\hat{\textbf{X}}-\mathcal{C}^{\beta,\hat\pi}$
—recall (3.2)—and because the distribution of
![]() $\hat X_n$
is absolutely continuous with respect to
$\hat X_n$
is absolutely continuous with respect to
![]() $\hat\lambda$
—see Lemma 3.1. From the Markov inequality we derive that
$\hat\lambda$
—see Lemma 3.1. From the Markov inequality we derive that
note that this bound does not depend on
![]() $\hat\pi\in\hat{\boldsymbol{\Pi}}_s$
. This shows (4.1).
$\hat\pi\in\hat{\boldsymbol{\Pi}}_s$
. This shows (4.1).
We now proceed with the proof. For each fixed
![]() $n\ge0$
, the mapping on
$n\ge0$
, the mapping on
![]() $(\textbf{X}\times\textbf{A})^{n-1}\times\textbf{X}$
given by
$(\textbf{X}\times\textbf{A})^{n-1}\times\textbf{X}$
given by
is in
![]() $\boldsymbol{\mathcal{U}}_n$
. Therefore, by the definition of the
$\boldsymbol{\mathcal{U}}_n$
. Therefore, by the definition of the
![]() $ws^\infty$
-topology, the function
$ws^\infty$
-topology, the function
is continuous on
![]() $\boldsymbol{\mathcal{S}}_{\nu}$
, and so the function
$\boldsymbol{\mathcal{S}}_{\nu}$
, and so the function
![]() $P\mapsto\int_{\boldsymbol{\Omega}}(1-\beta^{N_G})\textrm{d} P$
is lower semicontinuous on
$P\mapsto\int_{\boldsymbol{\Omega}}(1-\beta^{N_G})\textrm{d} P$
is lower semicontinuous on
![]() $\boldsymbol{\mathcal{S}}_{\nu}$
, since it is the increasing limit as
$\boldsymbol{\mathcal{S}}_{\nu}$
, since it is the increasing limit as
![]() $n\rightarrow\infty$
of continuous functions.
$n\rightarrow\infty$
of continuous functions.
Now we prove upper semicontinuity on
![]() $\boldsymbol{\mathcal{S}}_{\nu}^{s}$
. Fix arbitrary
$\boldsymbol{\mathcal{S}}_{\nu}^{s}$
. Fix arbitrary
![]() $0\le n\le m$
and
$0\le n\le m$
and
![]() $P\in \boldsymbol{\mathcal{S}}_{\nu}^{s}$
such that
$P\in \boldsymbol{\mathcal{S}}_{\nu}^{s}$
such that
![]() $P=\mathbb{P}^{\pi}_{\nu}$
for some
$P=\mathbb{P}^{\pi}_{\nu}$
for some
![]() $\pi\in\boldsymbol{\Pi}_{s}$
. Using Proposition 3.1,
$\pi\in\boldsymbol{\Pi}_{s}$
. Using Proposition 3.1,
 \begin{eqnarray*}\int_{\boldsymbol{\Omega}} (1-\beta^{N_G([0,m])}) \textrm{d}\mathbb{P}^{\pi}_{\nu}\, &=& \, (1-\beta)\mathbb{E}^{\beta,\pi^{\Delta}}_{\nu}[\hat{N}_G([0,m])] \\&\le&\, (1-\beta) \mathbb{E}^{\beta,\pi^{\Delta}}_{\nu}[\hat{N}_G([0,n])] \\&&+\, (1-\beta)\sup_{\hat{\pi}\in\hat{\boldsymbol{\Pi}}_{s}} \mathbb{E}^{\beta,\hat\pi}_{\nu}[\hat{N}_G([n+1,\infty))]\\&=& \, \int_{\boldsymbol{\Omega}} (1-\beta^{N_G([0,n])})\textrm{d} \mathbb{P}^{\pi}_{\nu}+\epsilon_n,\end{eqnarray*}
\begin{eqnarray*}\int_{\boldsymbol{\Omega}} (1-\beta^{N_G([0,m])}) \textrm{d}\mathbb{P}^{\pi}_{\nu}\, &=& \, (1-\beta)\mathbb{E}^{\beta,\pi^{\Delta}}_{\nu}[\hat{N}_G([0,m])] \\&\le&\, (1-\beta) \mathbb{E}^{\beta,\pi^{\Delta}}_{\nu}[\hat{N}_G([0,n])] \\&&+\, (1-\beta)\sup_{\hat{\pi}\in\hat{\boldsymbol{\Pi}}_{s}} \mathbb{E}^{\beta,\hat\pi}_{\nu}[\hat{N}_G([n+1,\infty))]\\&=& \, \int_{\boldsymbol{\Omega}} (1-\beta^{N_G([0,n])})\textrm{d} \mathbb{P}^{\pi}_{\nu}+\epsilon_n,\end{eqnarray*}
where we have defined
with
![]() $\epsilon_n\rightarrow0$
as a consequence of (4.1). By the result in [Reference Schäl27, Proposition 10.1], it follows that the limit as
$\epsilon_n\rightarrow0$
as a consequence of (4.1). By the result in [Reference Schäl27, Proposition 10.1], it follows that the limit as
![]() $n\rightarrow\infty$
of the function (4.2) is an upper semicontinous function on
$n\rightarrow\infty$
of the function (4.2) is an upper semicontinous function on
![]() $\boldsymbol{\mathcal{S}}_{\nu}^{s}$
. This completes the proof of the continuity statement on
$\boldsymbol{\mathcal{S}}_{\nu}^{s}$
. This completes the proof of the continuity statement on
![]() $\boldsymbol{\mathcal{S}}_{\nu}^{s}$
.
$\boldsymbol{\mathcal{S}}_{\nu}^{s}$
.
Proposition 4.2. Suppose that Assumptions A and B are satisfied and fix
![]() $0<\beta<1$
. There exists a stationary policy
$0<\beta<1$
. There exists a stationary policy
![]() $\hat{\pi}^*$
in
$\hat{\pi}^*$
in
![]() $\hat{\boldsymbol{\Pi}}_{s}$
that is optimal for the control model
$\hat{\boldsymbol{\Pi}}_{s}$
that is optimal for the control model
![]() $\mathcal{M}_{\beta}$
, i.e.,
$\mathcal{M}_{\beta}$
, i.e.,
Proof. Using the result in [Reference Schäl30, p. 368], we have
Consequently, from Proposition 3.1 we obtain
But the latter supremum is attained at some
![]() $P^*\in\boldsymbol{\mathcal{S}}^s_{\nu}$
, because it is the maximum of a continuous function (Proposition 4.1) on a compact set (Theorem 2.1). If
$P^*\in\boldsymbol{\mathcal{S}}^s_{\nu}$
, because it is the maximum of a continuous function (Proposition 4.1) on a compact set (Theorem 2.1). If
![]() $P^*=\mathbb{P}^{\pi_*}_{\nu}$
for some
$P^*=\mathbb{P}^{\pi_*}_{\nu}$
for some
![]() $\pi_*\in\boldsymbol{\Pi}_s$
, then we have that
$\pi_*\in\boldsymbol{\Pi}_s$
, then we have that
![]() $\pi_*^\Delta\in\hat{\boldsymbol{\Pi}}_s$
is an optimal stationary Markov policy for the control problem
$\pi_*^\Delta\in\hat{\boldsymbol{\Pi}}_s$
is an optimal stationary Markov policy for the control problem
![]() $\mathcal{M}_{\beta}$
.
$\mathcal{M}_{\beta}$
.
We are now in position to prove the main result of this paper, on maximizing the probability of visiting the set G infinitely often.
Theorem 4.1. Suppose that Assumptions A and B hold.
-
(i) There is some
 $\pi\in\boldsymbol{\Pi}_{s}$
that is optimal for the control model
$\pi\in\boldsymbol{\Pi}_{s}$
that is optimal for the control model
 $\mathcal{M}$
, that is,
$\mathcal{M}$
, that is,  \begin{align*}\mathbb{P}_{\nu}^{\pi}\{N_{G}=\infty\}=\sup_{\gamma\in\boldsymbol{\Pi}} \mathbb{P}_{\nu}^{\gamma}\{N_{G}=\infty\}=V^*(\nu).\end{align*}
\begin{align*}\mathbb{P}_{\nu}^{\pi}\{N_{G}=\infty\}=\sup_{\gamma\in\boldsymbol{\Pi}} \mathbb{P}_{\nu}^{\gamma}\{N_{G}=\infty\}=V^*(\nu).\end{align*}
-
(ii) Consider a sequence
 $\{\beta_k\}_{k\in\mathbb{N}}$
increasing to 1 and let
$\{\beta_k\}_{k\in\mathbb{N}}$
increasing to 1 and let
 $\hat{\pi}_{k}\in\hat{\boldsymbol{\Pi}}_{s}$
be an optimal policy for the model
$\hat{\pi}_{k}\in\hat{\boldsymbol{\Pi}}_{s}$
be an optimal policy for the model
 $\mathcal{M}_{\beta_k}$
. If
$\mathcal{M}_{\beta_k}$
. If
 $\hat{\pi}^{|\textbf{X}}_{k}\rightarrow{\pi}\in\boldsymbol{\Pi}_{s}$
in the narrow topology, then
$\hat{\pi}^{|\textbf{X}}_{k}\rightarrow{\pi}\in\boldsymbol{\Pi}_{s}$
in the narrow topology, then
 $\pi$
is optimal for
$\pi$
is optimal for
 $\mathcal{M}$
.
$\mathcal{M}$
. -
(iii) We have
 $\lim_{\beta\uparrow1} (1-\beta)V^*_{\beta}(\nu)=V^*(\nu)$
.
$\lim_{\beta\uparrow1} (1-\beta)V^*_{\beta}(\nu)=V^*(\nu)$
.
Proof. (i) Let
![]() $\{\beta_k\}_{k\in\mathbb{N}}$
be a sequence in (0, 1) with
$\{\beta_k\}_{k\in\mathbb{N}}$
be a sequence in (0, 1) with
![]() $\beta_k\uparrow1$
, and let the policy
$\beta_k\uparrow1$
, and let the policy
![]() $\hat{\pi}_{k}\in\hat{\boldsymbol{\Pi}}_{s}$
be optimal for
$\hat{\pi}_{k}\in\hat{\boldsymbol{\Pi}}_{s}$
be optimal for
![]() $\mathcal{M}_{\beta_k}$
. Such a policy exists by Proposition 4.2. Consider now the sequence
$\mathcal{M}_{\beta_k}$
. Such a policy exists by Proposition 4.2. Consider now the sequence
![]() $\{\pi_{k}\}_{k\in\mathbb{N}}$
in
$\{\pi_{k}\}_{k\in\mathbb{N}}$
in
![]() $\boldsymbol{\Pi}_{s}$
where
$\boldsymbol{\Pi}_{s}$
where
![]() $\pi_{k}=\hat{\pi}^{|\textbf{X}}_{k}$
for
$\pi_{k}=\hat{\pi}^{|\textbf{X}}_{k}$
for
![]() $k\in\mathbb{N}$
. The set
$k\in\mathbb{N}$
. The set
![]() $\boldsymbol{\Pi}_s$
being compact (Lemma 2.2), we have that
$\boldsymbol{\Pi}_s$
being compact (Lemma 2.2), we have that
![]() $\{\pi_{k}\}_{k\in\mathbb{N}}$
has a convergent subsequence, and we can assume without loss of generality that the whole sequence
$\{\pi_{k}\}_{k\in\mathbb{N}}$
has a convergent subsequence, and we can assume without loss of generality that the whole sequence
![]() $\{\pi_{k}\}_{k\in\mathbb{N}}$
converges to some
$\{\pi_{k}\}_{k\in\mathbb{N}}$
converges to some
![]() $\pi\in\boldsymbol{\Pi}_s$
. In particular, by Lemma 2.3, we also have
$\pi\in\boldsymbol{\Pi}_s$
. In particular, by Lemma 2.3, we also have
![]() $\mathbb{P}_{\nu}^{\pi_{k}}\Rightarrow \mathbb{P}_{\nu}^{\pi}$
.
$\mathbb{P}_{\nu}^{\pi_{k}}\Rightarrow \mathbb{P}_{\nu}^{\pi}$
.
By Proposition 3.1 it follows that for arbitrary
![]() $\gamma\in\boldsymbol{\Pi}$
,
$\gamma\in\boldsymbol{\Pi}$
,
 \begin{eqnarray*}\mathbb{E}_{\nu}^{\pi_k}[1-\beta_k^{N_G}] &=& \, (1-\beta_k) \mathbb{E}^{\beta_k,\hat{\pi}_{k}}_{\nu} [\hat{N}_G]\ =\ (1-\beta_k)V^*_{\beta_k}(\nu) \\ &\geq& (1-\beta_k) \mathbb{E}^{\beta_k,\gamma^{\Delta}}_{\nu} [\hat{N}_G]\ =\ \mathbb{E}_{\nu}^{\gamma}[1-\beta_k^{N_G}].\end{eqnarray*}
\begin{eqnarray*}\mathbb{E}_{\nu}^{\pi_k}[1-\beta_k^{N_G}] &=& \, (1-\beta_k) \mathbb{E}^{\beta_k,\hat{\pi}_{k}}_{\nu} [\hat{N}_G]\ =\ (1-\beta_k)V^*_{\beta_k}(\nu) \\ &\geq& (1-\beta_k) \mathbb{E}^{\beta_k,\gamma^{\Delta}}_{\nu} [\hat{N}_G]\ =\ \mathbb{E}_{\nu}^{\gamma}[1-\beta_k^{N_G}].\end{eqnarray*}
Now, by the first statement in Remark 3.2(b), observe that
and so for any
![]() $j\leq k$
in
$j\leq k$
in
![]() $\mathbb{N}$
we obtain the inequalities
$\mathbb{N}$
we obtain the inequalities
Taking the limit as
![]() $k\rightarrow\infty$
with j fixed in the previous inequalities, we get from Proposition 4.1 that
$k\rightarrow\infty$
with j fixed in the previous inequalities, we get from Proposition 4.1 that
In these inequalities, we take the limit as
![]() $j\rightarrow\infty$
and the supremum in
$j\rightarrow\infty$
and the supremum in
![]() $\gamma\in\boldsymbol{\Pi}$
to obtain
$\gamma\in\boldsymbol{\Pi}$
to obtain
Consequently, the above inequalities are all, in fact, equalities:
This establishes that the stationary Markov policy
![]() $\pi\in\boldsymbol{\Pi}_s$
is optimal for the control model
$\pi\in\boldsymbol{\Pi}_s$
is optimal for the control model
![]() $\mathcal{M}$
and that
$\mathcal{M}$
and that
![]() $(1-\beta_k)V^*_{\beta_k}(\nu)\rightarrow V^*(\nu)$
.
$(1-\beta_k)V^*_{\beta_k}(\nu)\rightarrow V^*(\nu)$
.
(ii) We can obtain the proof of this statement from the proof of (i), just by assuming that the whole sequence
![]() $\{\pi_k\}$
converges (and not invoking a convergent subsequence).
$\{\pi_k\}$
converges (and not invoking a convergent subsequence).
(iii) Using Proposition 3.1 we obtain that
This implies that
![]() $(1-\beta)V^*_{\beta}(\nu)$
decreases as
$(1-\beta)V^*_{\beta}(\nu)$
decreases as
![]() $\beta\uparrow1$
, and so
$\beta\uparrow1$
, and so
![]() $\lim_{\beta\uparrow1} (1-\beta)V^*_{\beta}(\nu)$
exists. Since we have convergence through some sequence of
$\lim_{\beta\uparrow1} (1-\beta)V^*_{\beta}(\nu)$
exists. Since we have convergence through some sequence of
![]() $\beta_k\uparrow1$
(recall (4.3)), the stated result follows.
$\beta_k\uparrow1$
(recall (4.3)), the stated result follows.
Summarizing, there indeed exists a stationary Markov policy in
![]() $\boldsymbol{\Pi}_{s}$
that maximizes the probability of visiting the set G infinitely often. This policy is obtained as an accumulation/limit point as
$\boldsymbol{\Pi}_{s}$
that maximizes the probability of visiting the set G infinitely often. This policy is obtained as an accumulation/limit point as
![]() $\beta\uparrow1$
in the sense of convergence of Young measures of optimal stationary Markov policies for the total-expected-reward problem
$\beta\uparrow1$
in the sense of convergence of Young measures of optimal stationary Markov policies for the total-expected-reward problem
![]() $\sup_{\hat{\pi}\in\hat{\boldsymbol{\Pi}}} \mathbb{E}_{\nu}^{\beta,\hat{\pi}}[\hat{N}_G]$
of the control model
$\sup_{\hat{\pi}\in\hat{\boldsymbol{\Pi}}} \mathbb{E}_{\nu}^{\beta,\hat{\pi}}[\hat{N}_G]$
of the control model
![]() $\mathcal{M}_{\beta}$
.
$\mathcal{M}_{\beta}$
.
Example 4.1. Consider a control model with state space
![]() $\textbf{X}=\{0,c,g,g_0,g_1,g_2,\ldots\}$
. There are two actions available at state 0, i.e.
$\textbf{X}=\{0,c,g,g_0,g_1,g_2,\ldots\}$
. There are two actions available at state 0, i.e.
![]() $\textbf{A}(0)=\{a_1,a_2\}$
, and there are no actions at the other states. The transition probabilities are
$\textbf{A}(0)=\{a_1,a_2\}$
, and there are no actions at the other states. The transition probabilities are
![]() $q(0,a_1,g_0)=1$
,
$q(0,a_1,g_0)=1$
,
![]() $q(0,a_2,c)=q(0,a_2,g)=1/2$
. From state
$q(0,a_2,c)=q(0,a_2,g)=1/2$
. From state
![]() $g_i$
, the transition probabilities are
$g_i$
, the transition probabilities are
while c and g are absorbing. Let
![]() $G=\{g,g_0,g_1,\ldots\}$
and let 0 be the initial state of the system. It should be clear that Assumption A holds.
$G=\{g,g_0,g_1,\ldots\}$
and let 0 be the initial state of the system. It should be clear that Assumption A holds.
Consider now the control model
![]() $\mathcal{M}_{\beta}$
. We identify
$\mathcal{M}_{\beta}$
. We identify
![]() $\hat{\boldsymbol{\Pi}}_s$
with the interval [0, 1], where
$\hat{\boldsymbol{\Pi}}_s$
with the interval [0, 1], where
![]() $0\le a\le 1$
stands for the probability of choosing action
$0\le a\le 1$
stands for the probability of choosing action
![]() $a_1$
at state 0. Let us verify the conditions in Proposition 3.2. Concerning (3.3), we put
$a_1$
at state 0. Let us verify the conditions in Proposition 3.2. Concerning (3.3), we put
![]() $W^{\beta,a}(c)=W^{\beta,a}(\Delta)=1$
and we let
$W^{\beta,a}(c)=W^{\beta,a}(\Delta)=1$
and we let
![]() $W^{\beta,a}$
be
$W^{\beta,a}$
be
![]() $+\infty$
in the remaining states, thus obtaining
$+\infty$
in the remaining states, thus obtaining
![]() $\mathcal{C}^{\beta,a}=\{c,\Delta\}$
, with
$\mathcal{C}^{\beta,a}=\{c,\Delta\}$
, with
![]() $\gamma^{\beta,a}=1$
. This identifies the transient and recurrent states of the Markov chain. For (3.5), we let
$\gamma^{\beta,a}=1$
. This identifies the transient and recurrent states of the Markov chain. For (3.5), we let
![]() $V^{\beta,a}(c)=V^{\beta,a}(\Delta)=0$
, and we try to find the minimal solution of (3.5). These inequalities become
$V^{\beta,a}(c)=V^{\beta,a}(\Delta)=0$
, and we try to find the minimal solution of (3.5). These inequalities become
and
By iteration of the latter inequalities we obtain
 \begin{align*}\frac{\beta^{i+1}}{(i+1)!}V^{\beta,a}(g_{i+1})\le V^{\beta,a}(g_0)-\sum_{j=0}^i \frac{\beta^j}{j!}.\end{align*}
\begin{align*}\frac{\beta^{i+1}}{(i+1)!}V^{\beta,a}(g_{i+1})\le V^{\beta,a}(g_0)-\sum_{j=0}^i \frac{\beta^j}{j!}.\end{align*}
The minimal solution is attained when
![]() $V^{\beta,a}(0)=e^\beta$
, and thus for any
$V^{\beta,a}(0)=e^\beta$
, and thus for any
![]() $i\ge0$
$i\ge0$
![]() $V^{\beta,a}(g)=\frac{1}{1-\beta}$
, and
$V^{\beta,a}(g)=\frac{1}{1-\beta}$
, and
We note that this minimal solution
![]() $V^{\beta,a}(x)$
is precisely the expected time the process spends in the transient states of the chain when starting from
$V^{\beta,a}(x)$
is precisely the expected time the process spends in the transient states of the chain when starting from
![]() $x\in\textbf{X}$
. We also note that
$x\in\textbf{X}$
. We also note that
![]() $V^{\beta,a}(x)$
is bounded in x (recall (3.4)): to see this, observe that
$V^{\beta,a}(x)$
is bounded in x (recall (3.4)): to see this, observe that
![]() $V^{\beta,a}(g_i)\le e^\beta$
for every
$V^{\beta,a}(g_i)\le e^\beta$
for every
![]() $i\ge0$
. It should be clear that the optimal value function of the control model
$i\ge0$
. It should be clear that the optimal value function of the control model
![]() $\mathcal{M}_{\beta}$
for the initial state 0 is
$\mathcal{M}_{\beta}$
for the initial state 0 is
and that the optimal policy is
![]() $\hat\pi^*_{\beta}=1$
for
$\hat\pi^*_{\beta}=1$
for
![]() $0<\beta\le \hat\beta$
and
$0<\beta\le \hat\beta$
and
![]() $\hat\pi^*_{\beta}=0$
for
$\hat\pi^*_{\beta}=0$
for
![]() $\hat\beta\le \beta<1$
, where
$\hat\beta\le \beta<1$
, where
![]() $\hat\beta\simeq 0.76804$
is the unique solution in (0, 1) of
$\hat\beta\simeq 0.76804$
is the unique solution in (0, 1) of
![]() $\frac{1}{2(1-z)}=e^{z}$
. The interesting feature of this example is that the optimal policy
$\frac{1}{2(1-z)}=e^{z}$
. The interesting feature of this example is that the optimal policy
![]() $\pi^*_{\beta}$
of
$\pi^*_{\beta}$
of
![]() $\mathcal{M}_{\beta}$
varies with
$\mathcal{M}_{\beta}$
varies with
![]() $\beta$
(cf. Example 3.1).
$\beta$
(cf. Example 3.1).
From Theorem 4.1(ii)–(iii) we obtain that
is an optimal policy for
![]() $\mathcal{M}$
and that
$\mathcal{M}$
and that
![]() $V^*(1)=\lim_{\beta\uparrow1} (1-\beta)V^*_{\beta}(1)=1/2$
.
$V^*(1)=\lim_{\beta\uparrow1} (1-\beta)V^*_{\beta}(1)=1/2$
.
Appendix A. Proof of Theorem 2.1
This section is mainly devoted to proving the compactness of
![]() $\boldsymbol{\mathcal{S}}_{\nu}^s$
, the compactness of
$\boldsymbol{\mathcal{S}}_{\nu}^s$
, the compactness of
![]() $\boldsymbol{\mathcal{S}}_{\nu}$
being a known result (see the proof of Theorem 2.1 below). In what follows, we suppose that Assumption A holds.
$\boldsymbol{\mathcal{S}}_{\nu}$
being a known result (see the proof of Theorem 2.1 below). In what follows, we suppose that Assumption A holds.
Lemma A.1. Suppose that
![]() $\textbf{Z}$
is a Borel space, and let
$\textbf{Z}$
is a Borel space, and let
![]() $f\,:\,\textbf{Z}\times\textbf{X}\times\textbf{A}\times\textbf{X}\rightarrow\mathbb{R}$
be bounded, measurable, and continuous on
$f\,:\,\textbf{Z}\times\textbf{X}\times\textbf{A}\times\textbf{X}\rightarrow\mathbb{R}$
be bounded, measurable, and continuous on
![]() $\textbf{A}$
when the remaining variables
$\textbf{A}$
when the remaining variables
![]() $z\in\textbf{Z}$
and
$z\in\textbf{Z}$
and
![]() $x,y\in\textbf{X}$
are fixed. Define the real-valued functions g and h on
$x,y\in\textbf{X}$
are fixed. Define the real-valued functions g and h on
![]() $\textbf{X}\times\textbf{K}$
and
$\textbf{X}\times\textbf{K}$
and
![]() $\textbf{Z}\times\textbf{X}$
respectively by
$\textbf{Z}\times\textbf{X}$
respectively by
Under these conditions, the following hold:
-
(i) The function g is bounded and measurable on
 $\textbf{Z}\times\textbf{K}$
, and
$\textbf{Z}\times\textbf{K}$
, and
 $g(z,x,\cdot)$
is continuous on
$g(z,x,\cdot)$
is continuous on
 $\textbf{A}(x)$
for fixed
$\textbf{A}(x)$
for fixed
 $(z,x)\in\textbf{Z}\times\textbf{X}$
.
$(z,x)\in\textbf{Z}\times\textbf{X}$
. -
(ii) The function h is bounded and measurable on
 $\textbf{Z}\times\textbf{X}$
.
$\textbf{Z}\times\textbf{X}$
.
Proof. (i) It is clear that g is bounded and measurable. To establish the continuity property, we fix
![]() $(z,x)\in\textbf{Z}\times\textbf{X}$
and consider a converging sequence
$(z,x)\in\textbf{Z}\times\textbf{X}$
and consider a converging sequence
![]() $a_n\rightarrow a$
in
$a_n\rightarrow a$
in
![]() $\textbf{A}$
. By the dominated convergence theorem, we have
$\textbf{A}$
. By the dominated convergence theorem, we have
![]() $f(z,x,a_n,\cdot) \ {\stackrel{*}{\rightharpoonup}\ } f(z,x,a,\cdot)$
in the weak
$f(z,x,a_n,\cdot) \ {\stackrel{*}{\rightharpoonup}\ } f(z,x,a,\cdot)$
in the weak
![]() $^{*}$
topology
$^{*}$
topology
![]() $\sigma(L^{\infty}(\textbf{X},\boldsymbol{\mathfrak{B}}(\textbf{X}),\lambda),L^{1}(\textbf{X},\boldsymbol{\mathfrak{B}}(\textbf{X}),\lambda))$
. We also have (recall Remark 2.1(b)) the convergence
$\sigma(L^{\infty}(\textbf{X},\boldsymbol{\mathfrak{B}}(\textbf{X}),\lambda),L^{1}(\textbf{X},\boldsymbol{\mathfrak{B}}(\textbf{X}),\lambda))$
. We also have (recall Remark 2.1(b)) the convergence
![]() $q(x,a_{n},\cdot)\stackrel{L^{1}}{\longrightarrow}q(x,a,\cdot)$
in norm in
$q(x,a_{n},\cdot)\stackrel{L^{1}}{\longrightarrow}q(x,a,\cdot)$
in norm in
![]() $L^{1}(\textbf{X},\boldsymbol{\mathfrak{B}}(\textbf{X}),\lambda)$
. Using the result in, e.g., [Reference Brezis11, Proposition 3.13.iv], we conclude that
$L^{1}(\textbf{X},\boldsymbol{\mathfrak{B}}(\textbf{X}),\lambda)$
. Using the result in, e.g., [Reference Brezis11, Proposition 3.13.iv], we conclude that
This completes the proof of the statement (i).
-
(iii) By Assumption (A.1) and the maximum measurable theorem [Reference Aliprantis and Border1, Theorem 18.19], we conclude that h is measurable.
Given
![]() $k\ge1$
, we say a function
$k\ge1$
, we say a function
![]() $f\,:\,(\textbf{X}\times\textbf{A})^{k}\times\textbf{X}\rightarrow\mathbb{R}$
is in
$f\,:\,(\textbf{X}\times\textbf{A})^{k}\times\textbf{X}\rightarrow\mathbb{R}$
is in
![]() $\boldsymbol{\mathcal{R}}_k$
if it is of the form
$\boldsymbol{\mathcal{R}}_k$
if it is of the form
where
![]() $\bar{f}\in\boldsymbol{\mathcal{B}}(\textbf{X}^{k+1})$
and
$\bar{f}\in\boldsymbol{\mathcal{B}}(\textbf{X}^{k+1})$
and
![]() $\bar{f}^{(i)}\in\boldsymbol{\mathcal{C}}(\textbf{A})$
for
$\bar{f}^{(i)}\in\boldsymbol{\mathcal{C}}(\textbf{A})$
for
![]() $0\le i<k$
. For
$0\le i<k$
. For
![]() $k=0$
we simply let
$k=0$
we simply let
![]() $\boldsymbol{\mathcal{R}}_0=\boldsymbol{\mathcal{B}}(\textbf{X})$
. Clearly,
$\boldsymbol{\mathcal{R}}_0=\boldsymbol{\mathcal{B}}(\textbf{X})$
. Clearly,
![]() $\boldsymbol{\mathcal{R}}_k\subseteq\boldsymbol{\mathcal{U}}_k$
. For any integer
$\boldsymbol{\mathcal{R}}_k\subseteq\boldsymbol{\mathcal{U}}_k$
. For any integer
![]() $k\ge1$
, define the operator
$k\ge1$
, define the operator
![]() $\mathfrak{A}_{k}\,:\, \boldsymbol{\mathcal{R}}_{k}\rightarrow \boldsymbol{\mathcal{R}}_{k-1}$
as follows. If
$\mathfrak{A}_{k}\,:\, \boldsymbol{\mathcal{R}}_{k}\rightarrow \boldsymbol{\mathcal{R}}_{k-1}$
as follows. If
![]() $f\in\boldsymbol{\mathcal{R}}_k$
then
$f\in\boldsymbol{\mathcal{R}}_k$
then
![]() $\mathfrak{A}_{k}f$
is given by
$\mathfrak{A}_{k}f$
is given by
 \begin{align}&(\mathfrak{A}_{k}f)(x_{0},a_{0},\ldots,x_{k-1}) =\max_{a\in\textbf{A}(x_{k-1})} \int_{\textbf{X}} f(x_{0},a_{0},\ldots,x_{k-1},a,y) q(x_{k-1},a,y)\lambda(dy)\nonumber \\&= \prod_{j=0}^{k-2} \bar{f}^{(j)}(a_j)\max_{a\in\textbf{A}(x_{k-1})} \int_{\textbf{X}} \bar{f}(x_{0},\ldots,x_{k-1},y) \bar{f}^{(k-1)}(a)q(x_{k-1},a,y)\lambda(dy)\end{align}
\begin{align}&(\mathfrak{A}_{k}f)(x_{0},a_{0},\ldots,x_{k-1}) =\max_{a\in\textbf{A}(x_{k-1})} \int_{\textbf{X}} f(x_{0},a_{0},\ldots,x_{k-1},a,y) q(x_{k-1},a,y)\lambda(dy)\nonumber \\&= \prod_{j=0}^{k-2} \bar{f}^{(j)}(a_j)\max_{a\in\textbf{A}(x_{k-1})} \int_{\textbf{X}} \bar{f}(x_{0},\ldots,x_{k-1},y) \bar{f}^{(k-1)}(a)q(x_{k-1},a,y)\lambda(dy)\end{align}
for
![]() $(x_0,a_0,\ldots,x_{k-1})\in(\textbf{X}\times\textbf{A})^{k-1}\times\textbf{X}$
, where by convention
$(x_0,a_0,\ldots,x_{k-1})\in(\textbf{X}\times\textbf{A})^{k-1}\times\textbf{X}$
, where by convention
![]() $\prod_{j=0}^{-1} \bar{f}^{(j)}(a_j)=1$
. Note that Lemma A.1(ii) ensures that
$\prod_{j=0}^{-1} \bar{f}^{(j)}(a_j)=1$
. Note that Lemma A.1(ii) ensures that
![]() $\mathfrak{A}_{k}$
indeed maps
$\mathfrak{A}_{k}$
indeed maps
![]() $\boldsymbol{\mathcal{R}}_{k}$
into
$\boldsymbol{\mathcal{R}}_{k}$
into
![]() $\boldsymbol{\mathcal{R}}_{k-1}$
because the
$\boldsymbol{\mathcal{R}}_{k-1}$
because the
![]() $\max$
in the right-hand-side of (A.1) is a measurable function of the variables
$\max$
in the right-hand-side of (A.1) is a measurable function of the variables
![]() $(x_0,\ldots,x_{k-1})\in\textbf{X}^k$
. In addition, we have that
$(x_0,\ldots,x_{k-1})\in\textbf{X}^k$
. In addition, we have that
![]() $\| \mathfrak{A}_kf\|\le \|f\|$
in their respective norms in
$\| \mathfrak{A}_kf\|\le \|f\|$
in their respective norms in
![]() $L^\infty$
. The successive composition of these operators is defined as
$L^\infty$
. The successive composition of these operators is defined as
so that
![]() $\mathfrak{T}_k\,:\,\boldsymbol{\mathcal{R}}_k\rightarrow\boldsymbol{\mathcal{R}}_0$
. By convention,
$\mathfrak{T}_k\,:\,\boldsymbol{\mathcal{R}}_k\rightarrow\boldsymbol{\mathcal{R}}_0$
. By convention,
![]() $\mathfrak{T}_0$
will be the identity operator on
$\mathfrak{T}_0$
will be the identity operator on
![]() $\boldsymbol{\mathcal{R}}_0$
.
$\boldsymbol{\mathcal{R}}_0$
.
Lemma A.2. Given any
![]() $k\ge0$
, and arbitrary
$k\ge0$
, and arbitrary
![]() $f\in\boldsymbol{\mathcal{R}}_k$
and
$f\in\boldsymbol{\mathcal{R}}_k$
and
![]() $\pi\in\boldsymbol{\Pi}$
, we have
$\pi\in\boldsymbol{\Pi}$
, we have
Proof. The stated result is trivial for
![]() $k=0$
. If
$k=0$
. If
![]() $k\ge1$
, observe that we can write
$k\ge1$
, observe that we can write
 \begin{align*}&\int_{(\textbf{X}\times\textbf{A})^{k}\times\textbf{X}} f(h_{k}) \mathbb{P}_{\nu,k}^{\pi}(h_{k}) = \int_{\textbf{H}_{k}} f(h_{k}) \mathbb{P}_{\nu,k}^{\pi}(h_{k}) \nonumber \\& = \int_{\textbf{H}_{k-1}} \int_{\textbf{A}(x_{k-1})}\int_{\textbf{X}} f(h_{k-1},a,y) q(x_{k-1},a,y) \lambda(dy) \pi_{k-1}(da|h_{k-1})\mathbb{P}_{\nu,k-1}^{\pi}(dh_{k-1}) \nonumber \\&\leq \int_{\textbf{H}_{k-1}} \mathfrak{A}_{k}f(h_{k-1}) \mathbb{P}_{\nu,k-1}^{\pi}(d h_{k-1}).\end{align*}
\begin{align*}&\int_{(\textbf{X}\times\textbf{A})^{k}\times\textbf{X}} f(h_{k}) \mathbb{P}_{\nu,k}^{\pi}(h_{k}) = \int_{\textbf{H}_{k}} f(h_{k}) \mathbb{P}_{\nu,k}^{\pi}(h_{k}) \nonumber \\& = \int_{\textbf{H}_{k-1}} \int_{\textbf{A}(x_{k-1})}\int_{\textbf{X}} f(h_{k-1},a,y) q(x_{k-1},a,y) \lambda(dy) \pi_{k-1}(da|h_{k-1})\mathbb{P}_{\nu,k-1}^{\pi}(dh_{k-1}) \nonumber \\&\leq \int_{\textbf{H}_{k-1}} \mathfrak{A}_{k}f(h_{k-1}) \mathbb{P}_{\nu,k-1}^{\pi}(d h_{k-1}).\end{align*}
By iterating this inequality and noting that
![]() $\mathbb{P}_{\nu,0}^\pi=\nu$
, we obtain the desired result.
$\mathbb{P}_{\nu,0}^\pi=\nu$
, we obtain the desired result.
Lemma A.3. For
![]() $k\ge1$
, suppose that we are given a sequence
$k\ge1$
, suppose that we are given a sequence
![]() $\{v_n\}_{n\in\mathbb{N}}$
in
$\{v_n\}_{n\in\mathbb{N}}$
in
![]() $\boldsymbol{\mathcal{R}}_k$
which is of the form
$\boldsymbol{\mathcal{R}}_k$
which is of the form
where
![]() $\bar{v}_n\in\boldsymbol{\mathcal{B}}(\textbf{X}^{k+1})$
satisfies
$\bar{v}_n\in\boldsymbol{\mathcal{B}}(\textbf{X}^{k+1})$
satisfies
![]() $\sup_n\|\bar{v}_n\|<\infty$
in
$\sup_n\|\bar{v}_n\|<\infty$
in
![]() $L^\infty$
and
$L^\infty$
and
and the functions
![]() $\bar{v}^{(i)}\in\boldsymbol{\mathcal{C}}(\textbf{A})$
for
$\bar{v}^{(i)}\in\boldsymbol{\mathcal{C}}(\textbf{A})$
for
![]() $0\le i<k$
do not depend on n. Under these conditions,
$0\le i<k$
do not depend on n. Under these conditions,
![]() $g_n=\mathfrak{A}_kv_n\in\boldsymbol{\mathcal{R}}_{k-1}$
can be written as
$g_n=\mathfrak{A}_kv_n\in\boldsymbol{\mathcal{R}}_{k-1}$
can be written as
where
![]() $\{\bar{g}_n\}_{n\in\mathbb{N}}$
is a sequence of functions in
$\{\bar{g}_n\}_{n\in\mathbb{N}}$
is a sequence of functions in
![]() $\boldsymbol{\mathcal{B}}(\textbf{X}^k)$
with
$\boldsymbol{\mathcal{B}}(\textbf{X}^k)$
with
![]() $\sup_n\|\bar{g}_n\|<\infty$
which satisfy that
$\sup_n\|\bar{g}_n\|<\infty$
which satisfy that
![]() $\bar{g}_n(x_0,\ldots,x_{k-1})\rightarrow0$
for any
$\bar{g}_n(x_0,\ldots,x_{k-1})\rightarrow0$
for any
![]() $(x_0,\ldots,x_{k-1})\in\textbf{X}^{k}$
as
$(x_0,\ldots,x_{k-1})\in\textbf{X}^{k}$
as
![]() $n\rightarrow\infty$
and, in particular,
$n\rightarrow\infty$
and, in particular,
Proof. The expression given for
![]() $g_n$
is easily deduced from (A.1). Moreover, the fact that
$g_n$
is easily deduced from (A.1). Moreover, the fact that
![]() $\{\bar{g}_n\}$
is bounded in the
$\{\bar{g}_n\}$
is bounded in the
![]() $L^\infty$
norm is also straightforward. To prove the limit property, we proceed by contradiction: we suppose that for some
$L^\infty$
norm is also straightforward. To prove the limit property, we proceed by contradiction: we suppose that for some
![]() $(x_0,\ldots,x_{k-1})$
and some subsequence
$(x_0,\ldots,x_{k-1})$
and some subsequence
![]() $\{n'\}$
there exists
$\{n'\}$
there exists
![]() $\epsilon>0$
with
$\epsilon>0$
with
Assuming that the above maximum is attained (recall Lemma A.1(ii)) at some
![]() $a^*_{n'}\in\textbf{A}(x_{k-1})$
, we may also suppose that
$a^*_{n'}\in\textbf{A}(x_{k-1})$
, we may also suppose that
![]() $a^*_{n'}\rightarrow a^*$
for some
$a^*_{n'}\rightarrow a^*$
for some
![]() $a^*\in\textbf{A}(x_{k-1})$
. Then we have the following convergences:
$a^*\in\textbf{A}(x_{k-1})$
. Then we have the following convergences:
To check the latter convergence, just note that
 \begin{align*}&\int_{\textbf{X}} \big|\bar{v}^{(k-1)}(a^*_{n'})q(x_{k-1},a^*_{n'},y)- \bar{v}^{(k-1)}(a^*)q(x_{k-1},a^*,y)\big|\lambda(dy)\\&\le \big|\bar{v}^{(k-1)}(a^*_{n'})-\bar{v}^{(k-1)}(a^*)\big|\int_{\textbf{X}} q(x_{k-1},a^*_{n'},y)\lambda(dy)\\&+\big|\bar{v}^{(k-1)}(a^*)\big| \int_{\textbf{X}}| q(x_{k-1},a^*_{n'},y)-q(x_{k-1},a^*,y)|\lambda(dy),\end{align*}
\begin{align*}&\int_{\textbf{X}} \big|\bar{v}^{(k-1)}(a^*_{n'})q(x_{k-1},a^*_{n'},y)- \bar{v}^{(k-1)}(a^*)q(x_{k-1},a^*,y)\big|\lambda(dy)\\&\le \big|\bar{v}^{(k-1)}(a^*_{n'})-\bar{v}^{(k-1)}(a^*)\big|\int_{\textbf{X}} q(x_{k-1},a^*_{n'},y)\lambda(dy)\\&+\big|\bar{v}^{(k-1)}(a^*)\big| \int_{\textbf{X}}| q(x_{k-1},a^*_{n'},y)-q(x_{k-1},a^*,y)|\lambda(dy),\end{align*}
which indeed converges to 0 as
![]() $n'\rightarrow\infty$
. Applying [Reference Brezis11, Proposition 3.13.iv], we obtain
$n'\rightarrow\infty$
. Applying [Reference Brezis11, Proposition 3.13.iv], we obtain
which is a contradiction. The last statement concerning the weak
![]() $^*$
convergence follows easily from dominated convergence, since
$^*$
convergence follows easily from dominated convergence, since
![]() $\{\bar{v}_n\}$
is uniformly bounded in the
$\{\bar{v}_n\}$
is uniformly bounded in the
![]() $L^\infty$
norm. This completes the proof.
$L^\infty$
norm. This completes the proof.
To summarize this lemma informally, note that if we have a sequence of the form
with
![]() $\{\bar{v}_n\}$
bounded and
$\{\bar{v}_n\}$
bounded and
![]() $v_n(x_0,\ldots,x_{k-1},\cdot)\ {\stackrel{*}{\rightharpoonup}\ }0$
, then
$v_n(x_0,\ldots,x_{k-1},\cdot)\ {\stackrel{*}{\rightharpoonup}\ }0$
, then
![]() $g_n=\mathfrak{A}_kv_n$
again satisfies the same properties, since
$g_n=\mathfrak{A}_kv_n$
again satisfies the same properties, since
with
![]() $\{\bar{g}_n\}$
bounded and
$\{\bar{g}_n\}$
bounded and
![]() $g_n(x_0,\ldots,x_{k-2},\cdot)\ {\stackrel{*}{\rightharpoonup}\ }0$
.
$g_n(x_0,\ldots,x_{k-2},\cdot)\ {\stackrel{*}{\rightharpoonup}\ }0$
.
Proof of Lemma 2.3. Suppose that we have a sequence
![]() $\{\gamma_{n}\}_{n\in\mathbb{N}}$
in
$\{\gamma_{n}\}_{n\in\mathbb{N}}$
in
![]() $\boldsymbol{\mathcal{Y}}$
converging to some
$\boldsymbol{\mathcal{Y}}$
converging to some
![]() $\gamma\in\boldsymbol{\mathcal{Y}}$
. We will show that
$\gamma\in\boldsymbol{\mathcal{Y}}$
. We will show that
![]() $\mathbb{P}^{\gamma_n}_{\nu}\Rightarrow\mathbb{P}^\gamma_{\nu}$
. To prove this result, it suffices to show that for any
$\mathbb{P}^{\gamma_n}_{\nu}\Rightarrow\mathbb{P}^\gamma_{\nu}$
. To prove this result, it suffices to show that for any
![]() $k\ge0$
and
$k\ge0$
and
![]() $f\in\boldsymbol{\mathcal{U}}_k$
, we have (recall (2.3))
$f\in\boldsymbol{\mathcal{U}}_k$
, we have (recall (2.3))
Also, by [Reference Schäl28, Theorem 3.7(ii)], it suffices to show (A.2) for functions f which are of the form
for
![]() $\bar{f}\in\boldsymbol{\mathcal{B}}(\textbf{X}^{k+1})$
and
$\bar{f}\in\boldsymbol{\mathcal{B}}(\textbf{X}^{k+1})$
and
![]() $\hat{f}\in\boldsymbol{\mathcal{C}}(\textbf{A}^{k})$
. As a preliminary step, we will establish the limit (A.2) for functions in
$\hat{f}\in\boldsymbol{\mathcal{C}}(\textbf{A}^{k})$
. As a preliminary step, we will establish the limit (A.2) for functions in
![]() $\boldsymbol{\mathcal{R}}_k$
, that is, those for which, in addition, the function
$\boldsymbol{\mathcal{R}}_k$
, that is, those for which, in addition, the function
![]() $\hat{f}$
in (A.3) is the product of k functions in
$\hat{f}$
in (A.3) is the product of k functions in
![]() $\boldsymbol{\mathcal{C}}(\textbf{A})$
, denoted by
$\boldsymbol{\mathcal{C}}(\textbf{A})$
, denoted by
![]() $\bar{f}^{(i)}$
for
$\bar{f}^{(i)}$
for
![]() $0\le i\le k-1$
.
$0\le i\le k-1$
.
We will prove the statement by induction. The limit in (A.2) trivially holds for
![]() $k=0$
because
$k=0$
because
![]() $\mathbb{P}^{\pi}_{\nu,0}=\nu$
for any
$\mathbb{P}^{\pi}_{\nu,0}=\nu$
for any
![]() $\pi\in\boldsymbol{\Pi}$
. Suppose that (A.2) is satisfied for some
$\pi\in\boldsymbol{\Pi}$
. Suppose that (A.2) is satisfied for some
![]() $k\ge0$
and every function in
$k\ge0$
and every function in
![]() $\boldsymbol{\mathcal{R}}_k$
, and let us prove it for
$\boldsymbol{\mathcal{R}}_k$
, and let us prove it for
![]() $k+1$
and any
$k+1$
and any
![]() $f\in\boldsymbol{\mathcal{R}}_{k+1}$
. We have
$f\in\boldsymbol{\mathcal{R}}_{k+1}$
. We have
 \begin{align} & \int_{\textbf{H}_{k+1}} f(h_{k+1}) \mathbb{P}_{\nu,k+1}^{\gamma_{n}}(dh_{k+1}) \nonumber \\& = \int_{\textbf{H}_{k}} \Big[ \int_{\textbf{A}}\int_{\textbf{X}} f(h_{k},a,y) q(x_{k},a,y) \lambda(dy) \gamma(da|x_{k}) \Big]\mathbb{P}_{\nu,k}^{\gamma_{n}}(dh_{k})\nonumber \\& \phantom{=} + \int_{\textbf{H}_{k}}\int_{\textbf{A}}\int_{\textbf{X}} f(h_{k},a,y) q(x_{k},a,y) \lambda(dy) \big[ \gamma_{n}(da|x_{k})-\gamma(da|x_{k}) \big]\mathbb{P}_{\nu,k}^{\gamma_{n}}(d h_{k}).\end{align}
\begin{align} & \int_{\textbf{H}_{k+1}} f(h_{k+1}) \mathbb{P}_{\nu,k+1}^{\gamma_{n}}(dh_{k+1}) \nonumber \\& = \int_{\textbf{H}_{k}} \Big[ \int_{\textbf{A}}\int_{\textbf{X}} f(h_{k},a,y) q(x_{k},a,y) \lambda(dy) \gamma(da|x_{k}) \Big]\mathbb{P}_{\nu,k}^{\gamma_{n}}(dh_{k})\nonumber \\& \phantom{=} + \int_{\textbf{H}_{k}}\int_{\textbf{A}}\int_{\textbf{X}} f(h_{k},a,y) q(x_{k},a,y) \lambda(dy) \big[ \gamma_{n}(da|x_{k})-\gamma(da|x_{k}) \big]\mathbb{P}_{\nu,k}^{\gamma_{n}}(d h_{k}).\end{align}
We study the limit of the first term in the right-hand-side of (A.4) as
![]() $n\rightarrow\infty$
. Since
$n\rightarrow\infty$
. Since
![]() $f\in\boldsymbol{\mathcal{R}}_{k+1}$
, we deduce from Lemma A.1(i) that the mapping defined on
$f\in\boldsymbol{\mathcal{R}}_{k+1}$
, we deduce from Lemma A.1(i) that the mapping defined on
![]() $(\textbf{X}\times\textbf{A})^{k}\times\textbf{X}$
by
$(\textbf{X}\times\textbf{A})^{k}\times\textbf{X}$
by
is in
![]() $\boldsymbol{\mathcal{R}}_{k}$
. By the induction hypothesis, we can take the limit as
$\boldsymbol{\mathcal{R}}_{k}$
. By the induction hypothesis, we can take the limit as
![]() $n\rightarrow\infty$
and so obtain
$n\rightarrow\infty$
and so obtain
 \begin{align*}\lim_{n\rightarrow\infty}&\int_{\textbf{H}_{k}} \Big[\int_{\textbf{A}} \int_{\textbf{X}} f(h_{k},a,y) q(x_{k},a,y) \lambda(dy) \gamma(da|x_{k}) \Big]\mathbb{P}_{\nu,k}^{\gamma_{n}}(dh_{k}) \\& = \int_{\textbf{H}_{k}} \Big[\int_{\textbf{A}} \int_{\textbf{X}} f(h_{k},a,y) q(x_{k},a,y) \lambda(dy) \gamma(da|x_{k}) \Big]\mathbb{P}_{\nu,k}^{\gamma}(dh_{k})\\&= \int_{\textbf{H}_{k+1}} f(h_{k+1})\mathbb{P}_{\nu,k+1}^{\gamma}(dh_{k+1}).\end{align*}
\begin{align*}\lim_{n\rightarrow\infty}&\int_{\textbf{H}_{k}} \Big[\int_{\textbf{A}} \int_{\textbf{X}} f(h_{k},a,y) q(x_{k},a,y) \lambda(dy) \gamma(da|x_{k}) \Big]\mathbb{P}_{\nu,k}^{\gamma_{n}}(dh_{k}) \\& = \int_{\textbf{H}_{k}} \Big[\int_{\textbf{A}} \int_{\textbf{X}} f(h_{k},a,y) q(x_{k},a,y) \lambda(dy) \gamma(da|x_{k}) \Big]\mathbb{P}_{\nu,k}^{\gamma}(dh_{k})\\&= \int_{\textbf{H}_{k+1}} f(h_{k+1})\mathbb{P}_{\nu,k+1}^{\gamma}(dh_{k+1}).\end{align*}
Our goal now is to show that the second term in the right-hand-side of (A.4) converges to zero as
![]() $n\rightarrow\infty$
. Observe that the function
$n\rightarrow\infty$
. Observe that the function
![]() $v_n$
on
$v_n$
on
![]() $(\textbf{X}\times\textbf{A})^{k}\times\textbf{X}$
defined as
$(\textbf{X}\times\textbf{A})^{k}\times\textbf{X}$
defined as
takes the particular form
(here, recall that
![]() $f=\bar{f}\cdot\bar{f}^{(0)}\cdots\bar{f}^{(k)}\in\boldsymbol{\mathcal{R}}_{k+1}$
), with
$f=\bar{f}\cdot\bar{f}^{(0)}\cdots\bar{f}^{(k)}\in\boldsymbol{\mathcal{R}}_{k+1}$
), with
Then
![]() $\{\bar{v}_n\}_{n\in\mathbb{N}}$
is a bounded sequence in
$\{\bar{v}_n\}_{n\in\mathbb{N}}$
is a bounded sequence in
![]() $\boldsymbol{\mathcal{B}}(\textbf{X}^{k+1})$
, and also
$\boldsymbol{\mathcal{B}}(\textbf{X}^{k+1})$
, and also
![]() $\bar{v}_n(x_0,\ldots,x_{k-1},\cdot)\ {\stackrel{*}{\rightharpoonup}\ }0$
for any
$\bar{v}_n(x_0,\ldots,x_{k-1},\cdot)\ {\stackrel{*}{\rightharpoonup}\ }0$
for any
![]() $(x_0,\ldots,x_{k-1})\in\textbf{X}^k$
. Indeed, given arbitrary
$(x_0,\ldots,x_{k-1})\in\textbf{X}^k$
. Indeed, given arbitrary
![]() $\Phi\in L^1(\textbf{X},\boldsymbol{\mathfrak{B}}(\textbf{X}),\lambda)$
we have
$\Phi\in L^1(\textbf{X},\boldsymbol{\mathfrak{B}}(\textbf{X}),\lambda)$
we have
 \begin{align*}&\int_{\textbf{X}} \bar{v}_n(x_0,\ldots,x_{k-1},z)\Phi(z)\lambda(dz)\\&=\int_{\textbf{X}}\int_{\textbf{A}} \Phi(z)\Big[\int_{\textbf{X}} \bar{f}(x_0,\ldots,z,y) \bar{f}^{(k)}(a) q(z,a,y) \lambda(dy) \Big]\big[ \gamma_{n}(da|z)-\gamma(da|z) \big]\lambda(dz).\end{align*}
\begin{align*}&\int_{\textbf{X}} \bar{v}_n(x_0,\ldots,x_{k-1},z)\Phi(z)\lambda(dz)\\&=\int_{\textbf{X}}\int_{\textbf{A}} \Phi(z)\Big[\int_{\textbf{X}} \bar{f}(x_0,\ldots,z,y) \bar{f}^{(k)}(a) q(z,a,y) \lambda(dy) \Big]\big[ \gamma_{n}(da|z)-\gamma(da|z) \big]\lambda(dz).\end{align*}
Noting that the integral within brackets is a bounded Carathéodory function in
![]() $z\in\textbf{X}$
and
$z\in\textbf{X}$
and
![]() $a\in\textbf{A}$
(recall Lemma A.1(i)), convergence to zero of the above integral follows from the definition of
$a\in\textbf{A}$
(recall Lemma A.1(i)), convergence to zero of the above integral follows from the definition of
![]() $\gamma_n\rightarrow\gamma$
in
$\gamma_n\rightarrow\gamma$
in
![]() $\boldsymbol{\mathcal{Y}}$
.
$\boldsymbol{\mathcal{Y}}$
.
We can therefore apply Lemma A.3 repeatedly to obtain that
![]() $\{\mathfrak{T}_k v_n\}_{n\in\mathbb{N}}$
is a bounded sequence in
$\{\mathfrak{T}_k v_n\}_{n\in\mathbb{N}}$
is a bounded sequence in
![]() $\boldsymbol{\mathcal{B}}(\textbf{X})$
such that
$\boldsymbol{\mathcal{B}}(\textbf{X})$
such that
![]() $\mathfrak{T}_kv_n(x_0) \rightarrow0$
for every
$\mathfrak{T}_kv_n(x_0) \rightarrow0$
for every
![]() $x_0\in\textbf{X}$
. By Lemma A.2 we obtain that the expression (A.4) satisfies the inequality
$x_0\in\textbf{X}$
. By Lemma A.2 we obtain that the expression (A.4) satisfies the inequality
 \begin{align*}&\int_{\textbf{H}_{k}}\int_{\textbf{A}}\int_{\textbf{X}} f(h_{k},a,y) q(x_{k},a,y) \lambda(dy) \big[ \gamma_{n}(da|x_{k})-\gamma(da|x_{k}) \big]\mathbb{P}_{\nu,k}^{\gamma_{n}}(d h_{k}) \\&=\int_{\textbf{H}_k} v_n(h_k)\mathbb{P}^{\gamma_n}_{\nu,k}(dh_k)\le \int_{\textbf{X}} \mathfrak{T}_k v_n d\nu,\end{align*}
\begin{align*}&\int_{\textbf{H}_{k}}\int_{\textbf{A}}\int_{\textbf{X}} f(h_{k},a,y) q(x_{k},a,y) \lambda(dy) \big[ \gamma_{n}(da|x_{k})-\gamma(da|x_{k}) \big]\mathbb{P}_{\nu,k}^{\gamma_{n}}(d h_{k}) \\&=\int_{\textbf{H}_k} v_n(h_k)\mathbb{P}^{\gamma_n}_{\nu,k}(dh_k)\le \int_{\textbf{X}} \mathfrak{T}_k v_n d\nu,\end{align*}
where the right-hand term converges to 0 as
![]() $n\rightarrow\infty$
. Using a symmetric argument for the function
$n\rightarrow\infty$
. Using a symmetric argument for the function
![]() $-f$
, we obtain that the above left-hand term converges to zero, and so (A.4) indeed tends to zero.
$-f$
, we obtain that the above left-hand term converges to zero, and so (A.4) indeed tends to zero.
So far, we have established the limit (A.2) for functions in
![]() $\boldsymbol{\mathcal{R}}_k$
. Note, however, that we can apply the Stone–Weierstrass theorem to the vector space spanned by the functions of the form
$\boldsymbol{\mathcal{R}}_k$
. Note, however, that we can apply the Stone–Weierstrass theorem to the vector space spanned by the functions of the form
![]() $\hat{f}(a_0,\ldots,a_{k-1})=\bar{f}^{(0)}(a_0)\cdots\bar{f}^{(k-1)}(a_{k-1})$
, which indeed separates points in
$\hat{f}(a_0,\ldots,a_{k-1})=\bar{f}^{(0)}(a_0)\cdots\bar{f}^{(k-1)}(a_{k-1})$
, which indeed separates points in
![]() $\textbf{A}^k$
, to obtain that the functions in
$\textbf{A}^k$
, to obtain that the functions in
![]() $\boldsymbol{\mathcal{C}}(\textbf{A}^k)$
can be uniformly approximated by functions in the above-mentioned vector space. Hence it is easy to establish that the limit in (A.2) holds for any function of the form (A.3). This completes the proof of Lemma 2.3.
$\boldsymbol{\mathcal{C}}(\textbf{A}^k)$
can be uniformly approximated by functions in the above-mentioned vector space. Hence it is easy to establish that the limit in (A.2) holds for any function of the form (A.3). This completes the proof of Lemma 2.3.
Proof of Theorem 2.1. By virtue of Assumption A, the control model
![]() $\mathcal{M}$
satisfies the conditions (S1) and (S2) in [Reference Balder3]. Therefore, combining Theorem 2.2, Lemma 2.4, and the proof of Proposition 3.2 in [Reference Balder3], it can be shown that the w-topology and the
$\mathcal{M}$
satisfies the conditions (S1) and (S2) in [Reference Balder3]. Therefore, combining Theorem 2.2, Lemma 2.4, and the proof of Proposition 3.2 in [Reference Balder3], it can be shown that the w-topology and the
![]() $ws^\infty$
-topology are identical on
$ws^\infty$
-topology are identical on
![]() $\boldsymbol{\mathcal{S}}_{\nu}$
. Consequently, the set
$\boldsymbol{\mathcal{S}}_{\nu}$
. Consequently, the set
![]() $\boldsymbol{\mathcal{S}}_{\nu}$
is compact for the ws
$\boldsymbol{\mathcal{S}}_{\nu}$
is compact for the ws
![]() $^\infty$
-topology by Theorem 2.1 in [Reference Balder3], and it is metrizable in this topology.
$^\infty$
-topology by Theorem 2.1 in [Reference Balder3], and it is metrizable in this topology.
To prove compactness of
![]() $\boldsymbol{\mathcal{S}}^s_{\nu}\subseteq\boldsymbol{\mathcal{S}}_{\nu}$
, we show that it is a closed subset of
$\boldsymbol{\mathcal{S}}^s_{\nu}\subseteq\boldsymbol{\mathcal{S}}_{\nu}$
, we show that it is a closed subset of
![]() $\boldsymbol{\mathcal{S}}_{\nu}$
. Suppose that we have a sequence
$\boldsymbol{\mathcal{S}}_{\nu}$
. Suppose that we have a sequence
![]() $\{\mathbb{P}_{\nu}^{\gamma_{n}}\}_{n\in\mathbb{N}}\subseteq\boldsymbol{\mathcal{S}}^s_{\nu}$
, where
$\{\mathbb{P}_{\nu}^{\gamma_{n}}\}_{n\in\mathbb{N}}\subseteq\boldsymbol{\mathcal{S}}^s_{\nu}$
, where
![]() $\gamma_{n}\in\boldsymbol{\mathcal{Y}}$
for each
$\gamma_{n}\in\boldsymbol{\mathcal{Y}}$
for each
![]() $n\in\mathbb{N}$
, converging to some probability measure
$n\in\mathbb{N}$
, converging to some probability measure
![]() $\mathbb{P}^\pi_{\nu}\in\boldsymbol{\mathcal{S}}_{\nu}$
for some
$\mathbb{P}^\pi_{\nu}\in\boldsymbol{\mathcal{S}}_{\nu}$
for some
![]() $\pi\in\boldsymbol{\Pi}$
. But
$\pi\in\boldsymbol{\Pi}$
. But
![]() $\boldsymbol{\mathcal{Y}}$
being a compact metric space, there exists a subsequence
$\boldsymbol{\mathcal{Y}}$
being a compact metric space, there exists a subsequence
![]() $\{n'\}$
of
$\{n'\}$
of
![]() $\{\gamma_n\}$
converging to some
$\{\gamma_n\}$
converging to some
![]() $\gamma\in\boldsymbol{\mathcal{Y}}$
. Since
$\gamma\in\boldsymbol{\mathcal{Y}}$
. Since
![]() $\mathbb{P}^{\gamma_{n'}}_{\nu}\Rightarrow\mathbb{P}^\gamma_{\nu}$
(Lemma 2.3), it follows that the limiting strategic probability measure
$\mathbb{P}^{\gamma_{n'}}_{\nu}\Rightarrow\mathbb{P}^\gamma_{\nu}$
(Lemma 2.3), it follows that the limiting strategic probability measure
![]() $\mathbb{P}^\gamma_{\nu}=\mathbb{P}^\pi_{\nu}$
is in
$\mathbb{P}^\gamma_{\nu}=\mathbb{P}^\pi_{\nu}$
is in
![]() $\boldsymbol{\mathcal{S}}^s_{\nu}$
. This completes the proof of Theorem 2.1.
$\boldsymbol{\mathcal{S}}^s_{\nu}$
. This completes the proof of Theorem 2.1.
Funding information
This work was supported by grant PID2021-122442NB-I00 from the Spanish Ministerio de Ciencia e Innovación.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article