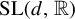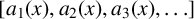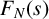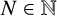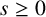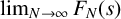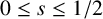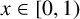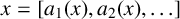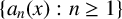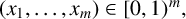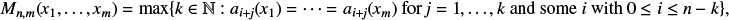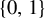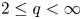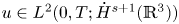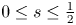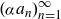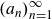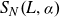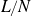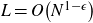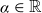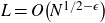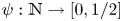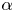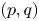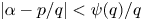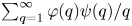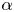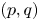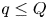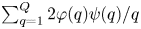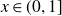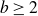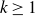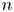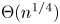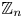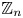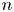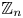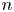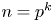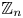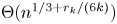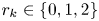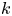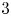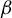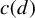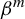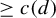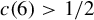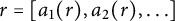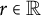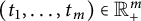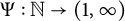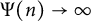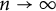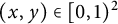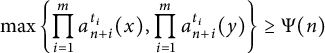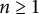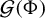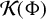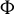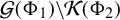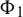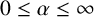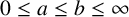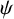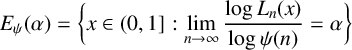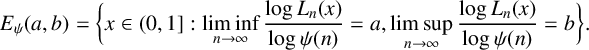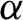162 results in 11Kxx
Poissonian pair correlation for directions in multi-dimensional affine lattices and escape of mass estimates for embedded horospheres
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 26 April 2024, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ASYMPTOTIC BEHAVIOUR FOR PRODUCTS OF CONSECUTIVE PARTIAL QUOTIENTS IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1-12
-
- Article
- Export citation
APPROXIMATION OF IRRATIONAL NUMBERS BY PAIRS OF INTEGERS FROM A LARGE SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 April 2024, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DIOPHANTINE TRANSFERENCE PRINCIPLE OVER FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 28 February 2024, pp. 1-18
-
- Article
- Export citation
ON THE N-POINT CORRELATION OF VAN DER CORPUT SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 15 September 2023, pp. 471-475
- Print publication:
- June 2024
-
- Article
- Export citation
ON THE SHORTEST DISTANCE FUNCTION IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 186-195
- Print publication:
- April 2024
-
- Article
- Export citation
Distribution and moments of the error term in the lattice point counting problem for three-dimensional Cygan–Korányi balls
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 19 May 2023, pp. 830-861
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polynomial mean complexity and logarithmic Sarnak conjecture
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 27 April 2023, pp. 769-798
- Print publication:
- March 2024
-
- Article
- Export citation
Fractal dimension of potential singular points set in the Navier–Stokes equations under supercritical regularity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 18 April 2023, pp. 727-745
- Print publication:
- June 2024
-
- Article
- Export citation
Intermediate-scale statistics for real-valued lacunary sequences
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 303-318
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hausdorff dimension of sets defined by almost convergent binary expansion sequences
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 13 March 2023, pp. 450-456
- Print publication:
- May 2023
-
- Article
- Export citation
Gaps between prime divisors and analogues in Diophantine geometry
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 27 February 2023, pp. S129-S147
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the metric theory of approximations by reduced fractions: a quantitative Koukoulopoulos–Maynard theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 03 February 2023, pp. 207-231
- Print publication:
- February 2023
-
- Article
- Export citation
Most numbers are not normal
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 1 / July 2023
- Published online by Cambridge University Press:
- 28 November 2022, pp. 1-11
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrepancy in modular arithmetic progressions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 01 December 2022, pp. 2082-2108
- Print publication:
- November 2022
-
- Article
- Export citation
Periodic expansion of one by Salem numbers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 14 October 2022, pp. 2841-2862
- Print publication:
- September 2023
-
- Article
- Export citation
A note on the relative growth of products of multiple partial quotients in the plane
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 19 August 2022, pp. 544-552
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hausdorff dimension of Dirichlet non-improvable set versus well-approximable set
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 04 August 2022, pp. 2707-2731
- Print publication:
- August 2023
-
- Article
- Export citation
ON LÜROTH EXPANSIONS IN WHICH THE LARGEST DIGIT GROWS WITH SLOWLY INCREASING SPEED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 23 June 2022, pp. 204-214
- Print publication:
- April 2023
-
- Article
- Export citation
Ergodicity of Iwasawa continued fractions via markable hyperbolic geodesics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 28 March 2022, pp. 1666-1711
- Print publication:
- May 2023
-
- Article
- Export citation