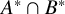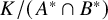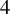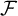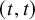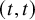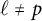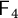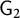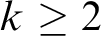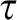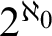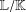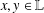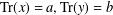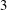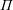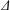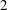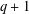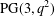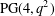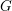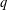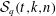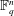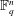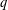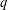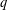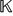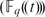41 results in 51Exx
A question of Frohardt on
 $2$-groups, skew translation quadrangles of even order and cyclic STGQs
$2$-groups, skew translation quadrangles of even order and cyclic STGQs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 06 December 2023, e109
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isogeny graphs on superspecial abelian varieties: eigenvalues and connection to Bruhat–Tits buildings
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 20 October 2023, pp. 1-26
-
- Article
- Export citation
Erdős–Ko–Rado theorem in Peisert-type graphs
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 04 August 2023, pp. 176-187
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Automorphisms and opposition in spherical buildings of exceptional type, I
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 05 July 2021, pp. 1517-1578
- Print publication:
- December 2022
-
- Article
- Export citation
On exceptional Lie geometries
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 11 January 2021, e2
-
- Article
-
- You have access
- Open access
- Export citation
STRONGLY MINIMAL STEINER SYSTEMS I: EXISTENCE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 October 2020, pp. 1486-1507
- Print publication:
- December 2021
-
- Article
- Export citation
ON THE PRODUCT OF ELEMENTS WITH PRESCRIBED TRACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 14 May 2020, pp. 264-288
- Print publication:
- April 2022
-
- Article
- Export citation
On sets of points with few odd secants
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 10 October 2019, pp. 31-43
-
- Article
- Export citation
Tits Triangles
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 15 November 2018, pp. 583-601
- Print publication:
- September 2019
-
- Article
- Export citation
CHARACTERIZING HERMITIAN VARIETIES IN THREE- AND FOUR-DIMENSIONAL PROJECTIVE SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 29 October 2018, pp. 1-8
- Print publication:
- August 2019
-
- Article
- Export citation
COORDINATISING PLANES OF PRIME POWER ORDER USING FINITE FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 22 August 2018, pp. 184-199
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
On Zeros of a Polynomial in a Finite Grid
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 3 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 310-333
-
- Article
- Export citation
COVERS OF GENERALIZED QUADRANGLES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 25 January 2018, pp. 585-601
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
SIMPLE GROUPS, PRODUCT ACTIONS, AND GENERALIZED QUADRANGLES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 234 / June 2019
- Published online by Cambridge University Press:
- 14 September 2017, pp. 87-126
- Print publication:
- June 2019
-
- Article
-
- You have access
- HTML
- Export citation
BRUCK NETS AND PARTIAL SHERK PLANES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 19 June 2017, pp. 1-12
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
EXISTENCE OF
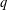 $q$-ANALOGS OF STEINER SYSTEMS
$q$-ANALOGS OF STEINER SYSTEMS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 4 / 2016
- Published online by Cambridge University Press:
- 30 August 2016, e7
-
- Article
-
- You have access
- Open access
- Export citation
A COMBINATORIAL CHARACTERIZATION OF THE LAGRANGIAN GRASSMANNIAN LG(3,6)(
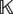 ${\mathbb{K}}$)
${\mathbb{K}}$)
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 293-311
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
Projective geometry in characteristic one and the epicyclic category
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 217 / March 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 95-132
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
COCOMPACT LATTICES ON Ãn BUILDINGS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 241-262
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
CONNECTEDNESS AND MINIMAL LENGTH ELEMENTS IN SPACES OF BOUNDED CURVATURE PATHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 05 June 2014, pp. 174-176
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation