Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-19T04:39:10.665Z Has data issue: false hasContentIssue false
  • English
  • Français

Automorphisms and opposition in spherical buildings of exceptional type, I

Part of: Structure and classification of infinite or finite groups Finite geometry and special incidence structures Nonlinear incidence geometry

Published online by Cambridge University Press:  05 July 2021

James Parkinson  and
Hendrik Van Maldeghem
James Parkinson*
Affiliation:
University of Sydney, Sydney, Australia
Hendrik Van Maldeghem
Affiliation:
Ghent University, Ghent, Belgium e-mail: Hendrik.VanMaldeghem@UGent.be
*
e-mail: jamesp@maths.usyd.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

To each automorphism of a spherical building, there is a naturally associated opposition diagram, which encodes the types of the simplices of the building that are mapped onto opposite simplices. If no chamber (that is, no maximal simplex) of the building is mapped onto an opposite chamber, then the automorphism is called domestic. 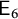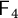In this paper, we give the complete classification of domestic automorphisms of split spherical buildings of types $\mathsf {E}_6$ , $\mathsf {F}_4$ , and 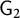$\mathsf {G}_2$ . Moreover, for all split spherical buildings of exceptional type, we classify (i) the domestic homologies, (ii) the opposition diagrams arising from elements of the standard unipotent subgroup of the Chevalley group, and (iii) the automorphisms with opposition diagrams with at most two distinguished orbits encircled. Our results provide unexpected characterizations of long root elations and products of perpendicular long root elations in long root geometries, and analogues of the density theorem for connected linear algebraic groups in the setting of Chevalley groups over arbitrary fields.

Keywords

Exceptional spherical buildingsopposition diagramdomestic automorphism

MSC classification

Primary: 20E42: Groups with a $BN$-pair; buildings
Secondary: 51E24: Buildings and the geometry of diagrams 51B25: Lie geometries 20E45: Conjugacy classes
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 6 , December 2022 , pp. 1517 - 1578
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramenko, P. and Brown, K., Buildings: theory and applications. Graduate Texts in Mathematics, 248, Springer, New York, 2008.CrossRefGoogle Scholar
Abramenko, P. and Brown, K., Automorphisms of non-spherical buildings have unbounded displacement. Innov. Incidence Geom. 10(2009), 1–13.Google Scholar
Bosma, W., Cannon, J., and Playoust, C., The Magma algebra system I: the user language. J. Symbolic Comput. 24(1997), 235–265.CrossRefGoogle Scholar
Bourbaki, N., Lie groups and Lie algebras, Chapters 4–6. Elements of Mathematics, Springer, New York, 2002.CrossRefGoogle Scholar
Carter, R., Simple groups of lie type. Wiley Classics Library, Wiley, New York, 1989.Google Scholar
Cohen, A. M., Murray, S. H., and Taylor, D. E., Computing in groups of Lie type. Math. Comp. 73(2004), no. 247, 1477–1498.CrossRefGoogle Scholar
De Schepper, A., Sastry, N. S. N., and Van Maldeghem, H., Split buildings of type F4 in buildings of type E6 . Abh. Math. Semin. Univ. Hambg. 88(2018), 97–160.Google Scholar
Humphreys, J. E., On the automorphisms of infinite Chevalley groups. Canad. J. Math. 21(1969), 908–911.CrossRefGoogle Scholar
Humphreys, J. E., Introduction to Lie algebras and representation theory. Graduate Texts in Mathematics, 9, Springer, New York, 1972.CrossRefGoogle Scholar
Humphreys, J. E., Linear algebraic groups. Graduate Texts in Mathematics, 21, Springer, New York, 1975.CrossRefGoogle Scholar
Ihringer, F., Sin, P., and Xiang, Q., New bounds for partial spreads of $\mathsf{H}\left(2d-1,{q}^2\right)$ and partial ovoids of the Ree–Tits octagon. J. Combin. Theory Ser. A 153(2018), 46–53.CrossRefGoogle Scholar
Liebeck, M. and Seitz, G., Unipotent and nilpotent classes in simple algebraic groups and Lie algebras. Mathematical Surveys and Monographs, 180, American Mathematical Society, Providence, RI, 2012.CrossRefGoogle Scholar
Parkinson, J., Ram, A., and Schwer, C., Combinatorics in affine flag varieties. J. Algebra 321(2009), 3469–3493.CrossRefGoogle Scholar
Parkinson, J., Temmermans, B., and Van Maldeghem, H., The combinatorics of automorphisms and opposition in generalised polygons. Ann. Comb. 19(2015), no. 3, 567–619.CrossRefGoogle Scholar
Parkinson, J. and Van Maldeghem, H., Opposition diagrams for automorphisms of large spherical buildings. J. Combin. Theory Ser. A 162(2019), 118–166.CrossRefGoogle Scholar
Parkinson, J. and Van Maldeghem, H., Opposition diagrams for automorphisms of small spherical buildings. Innov. Incidence Geom. 17(2019), 141–188.CrossRefGoogle Scholar
Parkinson, J. and Van Maldeghem, H., Automorphisms and opposition in spherical buildings of classical type. In preparation, 2020.Google Scholar
Parkinson, J., Van Maldeghem, H., and Victoor, M., Automorphisms and opposition in spherical buildings of exceptional type, II. In preparation, 2020.CrossRefGoogle Scholar
Petersson, H., Mühlherr, B., and Weiss, R., Descent in buildings. Annals of Mathematics Studies, 190, Princeton University Press, Princeton, NJ, 2015.Google Scholar
Scharlau, R., A structure theorem for weak buildings of spherical type. Geom. Dedicata 24(1987), 77–84.CrossRefGoogle Scholar
Shult, E., Points and lines: characterizing the classical geometries. Universitext, Springer, New York, 2010.Google Scholar
Steinberg, R., Automorphisms of finite linear groups. Canad. J. Math. 12(1960), 606–615.CrossRefGoogle Scholar
Steinberg, R., Lectures on Chevalley groups. University Lecture Series, 66, American Mathematical Society, Providence, RI, 2016.CrossRefGoogle Scholar
Temmermans, B., Thas, J. A., and Van Maldeghem, H., Domesticity in projective spaces. Innov. Incidence Geom. 12(2011), 141–149.Google Scholar
Temmermans, B., Thas, J. A., and Van Maldeghem, H., Collineations of polar spaces with restricted displacements. Des. Codes Cryptogr. 64(2012), 61–80.CrossRefGoogle Scholar
Temmermans, B., Thas, J. A., and Van Maldeghem, H., Domesticity in generalized quadrangles. Ann. Comb. 16(2012), 905–916.CrossRefGoogle Scholar
Timmesfeld, F. G., Structure and presentations of Lie-type groups. Proc. Lond. Math. Soc. 81(2000), 428–484.CrossRefGoogle Scholar
Tits, J., Buildings of spherical type and finite BN-pairs. Lecture Notes in Mathematics, 386, Springer, New York, 1974.Google Scholar
Tits, J., Moufang octagons and the Ree groups of type 2 F4 . Amer. J. Math. 105(1983), no. 2, 539–594.CrossRefGoogle Scholar
Van Maldeghem, H., Generalized polygons. Monographs in Mathematics, 93, Birkhäuser, Basel, Boston, and Berlin, 1998.Google Scholar
Van Maldeghem, H., Symplectic polarities of buildings of type E6 . Des. Codes Cryptogr. 65(2012), 115–125.CrossRefGoogle Scholar
Van Maldeghem, H., Characterizations of trialities of type Iid in buildings of type D4 . In: Sastry, N. S. N. (ed.), Groups of exceptional type, Coxeter groups, and related geometries, Springer Proceedings in Mathematics & Statistics, 82, Springer, New York, 2014, pp. 205–216.CrossRefGoogle Scholar