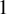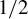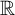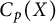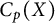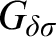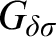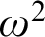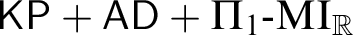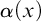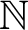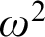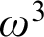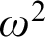85 results in 91Axx
Schmidt games and Cantor winning sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 19 April 2024, pp. 1-40
-
- Article
- Export citation
Game-theoretic policy computing and simulation for blockchained buffering system via diffusion approximation
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences , First View
- Published online by Cambridge University Press:
- 12 January 2024, pp. 1-36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear homeomorphisms of function spaces and the position of a space in its compactification
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1-22
-
- Article
- Export citation
Central limit theorem in complete feedback games
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 16 October 2023, pp. 654-666
- Print publication:
- June 2024
-
- Article
- Export citation
Tail variance allocation, Shapley value, and the majorization problem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 06 June 2023, pp. 153-171
- Print publication:
- March 2024
-
- Article
- Export citation
On asymptotic fairness in voting with greedy sampling
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 10 May 2023, pp. 999-1032
- Print publication:
- September 2023
-
- Article
- Export citation
THE MAGIC OF NASH SOCIAL WELFARE IN OPTIMIZATION: DO NOT SUM, JUST MULTIPLY!
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 07 July 2022, pp. 119-134
-
- Article
- Export citation
Semantics modulo satisfiability with applications: function representation, probabilities and game theory
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 28 June 2022, pp. 264-265
- Print publication:
- June 2022
-
- Article
-
- You have access
- Export citation
Nash equilibrium structure of Cox process Hotelling games
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 570-598
- Print publication:
- June 2022
-
- Article
- Export citation
Moment-constrained optimal dividends: precommitment and consistent planning
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 404-432
- Print publication:
- June 2022
-
- Article
- Export citation
ADVERSARIAL RISK ANALYSIS FOR FIRST-PRICE SEALED-BID AUCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 514-515
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
THE DISCONTINUITY PROBLEM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 03 January 2022, pp. 1191-1212
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
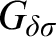 $G_{\delta \sigma }$
GAMES AND INDUCTION ON REALS
$G_{\delta \sigma }$
GAMES AND INDUCTION ON REALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 13 September 2021, pp. 1676-1690
- Print publication:
- December 2021
-
- Article
- Export citation
On the comparison of Shapley values for variance and standard deviation games
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 609-620
- Print publication:
- September 2021
-
- Article
- Export citation
GAMES AND CARDINALITIES IN INQUISITIVE FIRST-ORDER LOGIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 20 April 2021, pp. 241-267
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SHORTENING CLOPEN GAMES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1541-1554
- Print publication:
- December 2021
-
- Article
- Export citation
Comparing the best-reply strategy and mean-field games: The stationary case
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 20 November 2020, pp. 79-110
-
- Article
- Export citation
DOING WITHOUT ACTION TYPES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 21 October 2020, pp. 380-410
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maker–Breaker percolation games I: crossing grids
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 15 September 2020, pp. 200-227
-
- Article
-
- You have access
- Open access
- Export citation
Continuous-domain assignment flows
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 01 September 2020, pp. 570-597
-
- Article
- Export citation