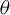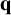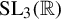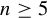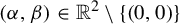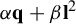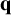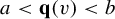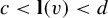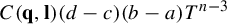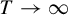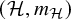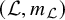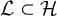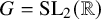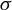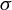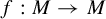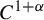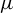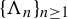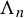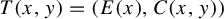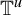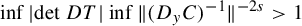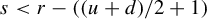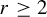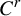208 results in 37Dxx
Distribution in homology classes and discrete fractal dimension
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Partially hyperbolic endomorphisms with expanding linear part
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
On invariant holonomies between centers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 08 May 2024, pp. 1-20
-
- Article
- Export citation
Non-invertible planar self-affine sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 08 May 2024, pp. 1-17
-
- Article
- Export citation
Weighted topological pressure revisited
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 08 May 2024, pp. 1-37
-
- Article
- Export citation
Asymptotic distribution for pairs of linear and quadratic forms at integral vectors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-29
-
- Article
- Export citation
On the ergodic theory of the real Rel foliation
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scale recurrence lemma and dimension formula for Cantor sets in the complex plane
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 25 March 2024, pp. 1-42
-
- Article
- Export citation
Rigidity of pressures of Hölder potentials and the fitting of analytic functions through them
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 18 March 2024, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THERMODYNAMIC FORMALISM FOR AMENABLE GROUPS AND COUNTABLE STATE SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 15 March 2024, pp. 1-65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Patterson–Sullivan theory for groups with a strongly contracting element
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 05 March 2024, pp. 1-56
-
- Article
- Export citation
DIOPHANTINE TRANSFERENCE PRINCIPLE OVER FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 28 February 2024, pp. 1-18
-
- Article
- Export citation
Upper, down, two-sided Lorenz attractor, collisions, merging, and switching
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 21 February 2024, pp. 1-45
-
- Article
- Export citation
Dimension estimates and approximation in non-uniformly hyperbolic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 12 February 2024, pp. 1-27
-
- Article
- Export citation
Regularity and linear response formula of the SRB measures for solenoidal attractors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 06 February 2024, pp. 1-50
-
- Article
- Export citation
Joint partial equidistribution of Farey rays in negatively curved manifolds and trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 08 January 2024, pp. 1-37
-
- Article
- Export citation
BRATTELI–VERSHIKISABILITY OF POLYGONAL BILLIARDS ON THE HYPERBOLIC PLANE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 15 December 2023, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting geodesics of given commutator length
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 15 December 2023, e114
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equilibrium states for non-uniformly expanding skew products
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 11 December 2023, pp. 1-22
-
- Article
- Export citation
Constructing Birkhoff sections for pseudo-Anosov flows with controlled complexity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 14 November 2023, pp. 1-53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation