Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-27T12:59:45.236Z Has data issue: false hasContentIssue false
  • English
  • Français

Dimension estimates and approximation in non-uniformly hyperbolic systems

Part of: Smooth dynamical systems: general theory Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  12 February 2024

JUAN WANG ,
YONGLUO CAO  and
YUN ZHAO
JUAN WANG
Affiliation:
School of Mathematics, Physics and Statistics, Shanghai University of Engineering Science, Shanghai 201620, P.R. China (e-mail: wangjuanmath@sues.edu.cn)
YONGLUO CAO
Affiliation:
Department of Mathematics, Soochow University, Suzhou 215006, Jiangsu, P.R. China Center for Dynamical Systems and Differential Equations, Soochow University, Suzhou 215006, Jiangsu, P.R. China (e-mail: ylcao@suda.edu.cn)
YUN ZHAO*
Affiliation:
Center for Dynamical Systems and Differential Equations, Soochow University, Suzhou 215006, Jiangsu, P.R. China (e-mail: ylcao@suda.edu.cn) School of Mathematical Sciences, Soochow University, Suzhou 215006, Jiangsu, P.R. China
*
e-mail: zhaoyun@suda.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 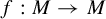$f: M\rightarrow M$ be a 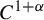$C^{1+\alpha }$ diffeomorphism on an 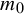$m_0$-dimensional compact smooth Riemannian manifold M and 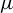$\mu $ a hyperbolic ergodic f-invariant probability measure. This paper obtains an upper bound for the stable (unstable) pointwise dimension of 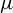$\mu $, which is given by the unique solution of an equation involving the sub-additive measure-theoretic pressure. If 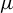$\mu $ is a Sinai–Ruelle–Bowen (SRB) measure, then the Kaplan–Yorke conjecture is true under some additional conditions and the Lyapunov dimension of 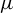$\mu $ can be approximated gradually by the Hausdorff dimension of a sequence of hyperbolic sets 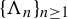$\{\Lambda _n\}_{n\geq 1}$. The limit behaviour of the Carathéodory singular dimension of 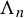$\Lambda _n$ on the unstable manifold with respect to the super-additive singular valued potential is also studied.

Keywords

dimensionhyperbolic measurehyperbolic set

MSC classification

Primary: 37C45: Dimension theory of dynamical systems 37D25: Nonuniformly hyperbolic systems (Lyapunov exponents, Pesin theory, etc.)
Secondary: 37D20: Uniformly hyperbolic systems (expanding, Anosov, Axiom A, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , First View , pp. 1 - 27
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdenur, F., Bonatti, C. and Crovisier, S.. Nonuniform hyperbolicity for ${C}^1$ -generic diffeomorphisms. Israel J. Math. 183 (2011), 1–60.CrossRefGoogle Scholar
Avila, A., Crovisier, S. and Wilkinson, A.. ${C}^1$ density of stable ergodicity. Adv. Math. 379 (2021), 107496.CrossRefGoogle Scholar
Ban, J., Cao, Y. and Hu, H.. The dimension of a non-conformal repeller and an average conformal repeller. Trans. Amer. Math. Soc. 362 (2010), 727–751.CrossRefGoogle Scholar
Barreira, L., Pesin, Y. and Schmeling, J.. Dimension and product structure of hyperbolic measures. Ann. of Math. (2) 149(3) (1999), 755–783.CrossRefGoogle Scholar
Barreira, L. and Wolf, C.. Pointwise dimension and ergodic decompositions. Ergod. Th. & Dynam. Sys. 26 (2006), 653–671.CrossRefGoogle Scholar
Cao, Y., Feng, D. and Huang, W.. The thermodynamic formalism for sub-additive potentials. Discrete Contin. Dyn. Syst. 20 (2008), 639–657.CrossRefGoogle Scholar
Cao, Y., Hu, H. and Zhao, Y.. Nonadditive measure-theoretic pressure and applications to dimensions of an ergodic measure. Ergod. Th. & Dynam. Sys. 33(3) (2013), 831–850.CrossRefGoogle Scholar
Cao, Y., Pesin, Y. and Zhao, Y.. Dimension estimates for non-conformal repellers and continuity of sub-additive topological pressure. Geom. Funct. Anal. 29 (2019), 1325–1368.CrossRefGoogle Scholar
Cao, Y., Wang, J. and Zhao, Y.. Dimension approximation in smooth dynamical systems. Ergod. Th. & Dynam. Sys. 44 (2024), 383–407.CrossRefGoogle Scholar
Chung, Y.. Shadowing properties of non-invertible maps with hyperbolic measures. Tokyo J. Math. 22 (1999), 145–166.CrossRefGoogle Scholar
Climenhaga, V., Pesin, Y. and Zelerowicz, A.. Equilibrium states in dynamical systems via geometric measure theory. Bull. Amer. Math. Soc. (N.S.) 56(4) (2019), 569–610.CrossRefGoogle Scholar
Fang, J., Cao, Y. and Zhao, Y.. Measure theoretic pressure and dimension formula for non-ergodic measures. Discrete Contin. Dyn. Syst. 40(5) (2020), 2767–2789.CrossRefGoogle Scholar
Frederickson, P., Kaplan, J., Yorke, E. and Yorke, J.. The Lyapunov dimension of strange attractors. J. Differential Equations 49(2) (1983), 185–207.CrossRefGoogle Scholar
Gelfert, K.. Repellers for non-uniformly expanding maps with singular or critical points. Bull. Braz. Math. Soc. (N.S.) 41 (2010), 237–257.CrossRefGoogle Scholar
Gelfert, K.. Horseshoes for diffeomorphisms preserving hyperbolic measures. Math. Z. 283 (2016), 685–701.CrossRefGoogle Scholar
He, L., Lv, J. and Zhou, L.. Definition of measure-theoretic pressure using spanning sets. Acta Math. Sin. (Engl. Ser.) 20(4) (2004), 709–718.CrossRefGoogle Scholar
Jordan, T. and Pollicott, M.. The Hausdorff dimension of measures for iterated function systems which contract on average. Discrete Contin. Dyn. Syst. 22 (2012), 235–246.Google Scholar
Katok, A.. Lyapunov exponents, entropy and periodic orbits for diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 51 (1980), 137–173.CrossRefGoogle Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and Its Applications, 54). Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Ledrappier, F.. Dimension of invariant measures. Proceedings of the Conference on Ergodic Theory and Related Topics, II (Georgenthal, 1986) (Mathematics in Stuttgart, 94). Eds. H. Michel, K. Häsler and V. Warstat. Teubner-Tecte, Leipzig, 1987, pp. 116–124.Google Scholar
Ledrappier, F. and Young, L. S.. The metric entropy of diffeomorphisms. I. Ann. of Math. (2) 122(3) (1985), 509–539.CrossRefGoogle Scholar
Ledrappier, F. and Young, L. S.. The metric entropy of diffeomorphisms. II. Relations between entropy, exponents and dimension. Ann. of Math. (2) 122(3) (1985), 540–574.CrossRefGoogle Scholar
Mañé, R.. A proof of Pesin’s formula. Ergod. Th. & Dynam. Sys. 1 (1981), 95–102.CrossRefGoogle Scholar
Mendoza, L.. Ergodic attractors for diffeomorphisms of surfaces. J. Lond. Math. Soc. (2) 37 (1988), 362–374.CrossRefGoogle Scholar
Misiurewicz, M. and Szlenk, W.. Entropy of piecewise monotone mappings. Studia Math. 67 (1980), 45–63.CrossRefGoogle Scholar
Oseledets, V.. A multiplicative ergodic theorem. Trans. Moscow Math. Soc. 19 (1968), 197–231.Google Scholar
Persson, T. and Schmeling, J.. Dyadic diophantine approximation and Katok’s horseshoe approximation. Acta Arith. 132 (2008), 205–230.CrossRefGoogle Scholar
Pesin, Y.. Characteristic Lyapunov exponents and smooth ergodic theory. Russian Math. Surveys 32 (1977), 55–114.CrossRefGoogle Scholar
Pesin, Y.. Dimension Theory in Dynamical Systems. Contemporary Views and Applications (Chicago Lectures in Mathematics). University of Chicago Press, Chicago, IL, 1997.CrossRefGoogle Scholar
Przytycki, F. and Urbański, M.. Conformal Fractals: Ergodic Theory Methods (London Mathematical Society Lecture Note Series, 371). Cambridge University Press, Cambridge, 2010.CrossRefGoogle Scholar
Sánchez-Salas, F. J.. Ergodic attractors as limits of hyperbolic horseshoes. Ergod. Th. & Dynam. Sys. 22(2) (2002), 571–589.CrossRefGoogle Scholar
Shu, L.. Dimension theory for invariant measures of endomorphisms. Comm. Math. Phys. 298 (2010), 65–99.CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory. Springer-Verlag, New York, 1982.CrossRefGoogle Scholar
Wang, J., Qu, C. and Cao, Y.. Dimension approximation for diffeomorphisms preserving hyperbolic SRB measures. J. Differential Equations 337 (2022), 294–322.CrossRefGoogle Scholar
Yang, Y.. Horseshoes for ${C}^{1+\alpha }$ mappings with hyperbolic measures. Discrete Contin. Dyn. Syst. 35 (2015), 5133–5152.CrossRefGoogle Scholar
Young, L. S.. Dimension, entropy and Lyapunov exponents. Ergod. Th. & Dynam. Sys. 2 (1982), 109–129.CrossRefGoogle Scholar