Hostname: page-component-76fb5796d-5g6vh Total loading time: 0 Render date: 2024-04-27T09:29:52.871Z Has data issue: false hasContentIssue false
  • English
  • Français

Regularity and linear response formula of the SRB measures for solenoidal attractors

Part of: Dynamical systems with hyperbolic behavior Smooth dynamical systems: general theory

Published online by Cambridge University Press:  06 February 2024

CARLOS BOCKER ,
RICARDO BORTOLOTTI Open the ORCID record for RICARDO BORTOLOTTI [Opens in a new window]  and
ARMANDO CASTRO Open the ORCID record for ARMANDO CASTRO [Opens in a new window]
CARLOS BOCKER
Affiliation:
Department of Mathematics, UFPB, João Pessoa, PB, Brazil (e-mail: cbocker@gmail.com)
RICARDO BORTOLOTTI*
Affiliation:
Department of Mathematics, UFPE, Recife, PE, Brazil
ARMANDO CASTRO
Affiliation:
Department of Mathematics, UFBA, Salvador, BA, Brazil (e-mail: armandomath@gmail.com)
*
e-mail: ricardo.bortolotti@ufpe.br
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that a class of higher-dimensional hyperbolic endomorphisms admit absolutely continuous invariant probabilities whose densities are regular and vary differentiably with respect to the dynamical system. The maps we consider are skew-products given by 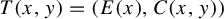$T(x,y) = (E (x), C(x,y))$, where E is an expanding map of 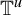$\mathbb {T}^u$ and C is a contracting map on each fiber. If 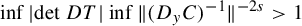$\inf |\!\det DT| \inf \| (D_yC)^{-1}\| ^{-2s}>1$ for some 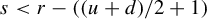${s<r-(({u+d})/{2}+1)}$, 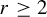$r \geq 2$, and T satisfies a transversality condition between overlaps of iterates of T (a condition which we prove to be 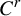$C^r$-generic under mild assumptions), then the SRB measure 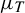$\mu _T$ of T is absolutely continuous and its density 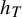$h_T$ belongs to the Sobolev space 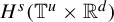$H^s({\mathbb {T}}^u\times {\mathbb {R}}^d)$. When 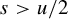$s> {u}/{2}$, it is also valid that the density 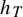$h_T$ is differentiable with respect to T. Similar results are proved for thermodynamical quantities for potentials close to the geometric potential.

Keywords

Solenoidal attractorstransversality conditionlinear response formulathermodynamical formalism

MSC classification

Primary: 37C40: Smooth ergodic theory, invariant measures 37C30: Zeta functions, (Ruelle-Frobenius) transfer operators, and other functional analytic techniques in dynamical systems 37D20: Uniformly hyperbolic systems (expanding, Anosov, Axiom A, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , First View , pp. 1 - 50
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, R.. Sobolev Spaces (Pure and Applied Mathematics, 65). Academic Press, New York, 1975.Google Scholar
Adler, R.. F-expansions revisited. Recent Advances in Topological Dynamics (Lecture Notes in Mathematics, 318). Ed. Beck, A.. Springer-Verlag, New York, 1975, pp. 1–5.Google Scholar
Alexander, J. and Yorke, J.. Fat Baker’s transformations. Ergod. Th. & Dynam. Sys. 4 (1984), 1–23.CrossRefGoogle Scholar
Alves, J.. SRB measures for non-hyperbolic systems with multidimensional expansion. Ann. Sci. Éc. Norm. Supér. (4) 33 (2000), 1–32.CrossRefGoogle Scholar
Alves, J. and Pinheiro, V.. Topological structure of (partially) hyperbolic sets with positive volume. Trans. Amer. Math. Soc. 360 (2008), 5551–5569.CrossRefGoogle Scholar
Andersson, M.. Robust ergodic properties in partially hyperbolic dynamics. Trans. Amer. Math. Soc. 362(4) (2010), 1831–1867.Google Scholar
Avila, A., Gouezel, S. and Tsujii, M.. Smoothness of solenoidal attractors. Discrete Contin. Dyn. Syst. 15 (2006), 21–35.Google Scholar
Baladi, V.. Linear response, or else. Proceedings of the International Congress of Mathematicians (Seoul 2014). Vol. III. Eds. S. Y. Jang, Y. R. Kim, D.-W. Lee and I. Yie. Kyung Moon Sa, Seoul, ICM, 2014, pp. 525–545.Google Scholar
Baladi, V. and Tsujii, M.. Anisotropic Holder and Sobolev spaces for hyperbolic diffeomorphisms. Ann. Inst. Fourier (Grenoble) 57(1) (2007), 127–154.Google Scholar
Barreira, L.. Ergodic Theory, Hyperbolic Dynamics and Dimension Theory (Universitext). Springer, Berlin, 2012.CrossRefGoogle Scholar
Blank, M., Keller, G. and Liverani, C.. Ruelle–Perron–Frobenius spectrum for Anosov maps. Nonlinearity 15(6) (2002), 1905–1973.Google Scholar
Bocker, C. and Bortolotti, R.. Higher-dimensional Attractors with absolutely continuous invariant probability. Nonlinearity 31 (2018), 2057–2082.Google Scholar
Bomfim, T. and Castro, A.. Linear response, and consequences for differentiability of statistical quantities and multifractal analysis. J. Stat. Phys. 174 (2019), 135–159.Google Scholar
Bomfim, T., Castro, A. and Varandas, P.. Differentiability of thermodynamical quantities in nonuniformly expanding dynamics. Adv. Math. 292 (2016), 478–528.CrossRefGoogle Scholar
Bortolotti, R. and Silva, E.. Hausdorff dimension of thin higher-dimensional solenoidal attractors. Nonlinearity 35 (2022), 3261–3282.Google Scholar
Bortolotti, R. and Silva, E.. Dimension of a class of intrinsically transversal solenoidal attractors in high dimensions. Qual. Theory Dyn. Syst. 21 (2022), 156.CrossRefGoogle Scholar
Bothe, H.. The Hausdorff dimension of certain solenoids. Ergod. Th. & Dynam. Sys. 15 (1995), 449–474.Google Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470). Springer-Verlag, Berlin, 1975.CrossRefGoogle Scholar
Bowen, R. and Ruelle, D.. The ergodic theory of Axiom A flows. Invent. Math. 29 (1975), 181–202.CrossRefGoogle Scholar
Chandler-Wilde, S. N., Hewett, D. P. and Moiola, A.. Interpolation of Hilbert and Sobolev spaces: quantitatives estimates and counterexamples. Mathematika 61 (2015), 414–443.Google Scholar
Cruz, A. and Varandas, P.. SRB measures for partially hyperbolic attractors of local diffeomorphisms. Ergod. Th. & Dynam. Sys. 40(6) (2020), 1545–1593.Google Scholar
Demers, M., Kiamari, N. and Liverani, C.. Transfer Operators in Hyperbolic Dynamics: An Introduction (33 Colóquio Brasileiro de Matemática). Rio de Janeiro, Brazil, Editora do IMPA, 2021.Google Scholar
Franks, J.. Manifolds of ${C}^r$ mappings and applications to differentiable dynamical systems. Studies in Analysis (Advances in Mathematics Supplementary Studies, 4). Academic Press, New York, 1979, pp. 271–290.Google Scholar
Gouezel, S. and Liverani, C.. Banach spaces adapted to Anosov systems. Ergod. Th. & Dynam. Sys. 26 (2006), 189–217.Google Scholar
Gouezel, S. and Liverani, C.. Compact locally maximal hyperbolic sets for smooth maps: fine statistical properties. J. Diff. Geom. 79 (2008), 433–477.Google Scholar
Hennion, H.. Sur un théorème spectral et son application aux noyaux lipschitiens. Proc. Amer. Math. Soc. 118 (1993), 627–634.Google Scholar
Hormander, L.. The Analysis of Linear Partial Differential Operators I, 2nd edn. Springer-Verlag, Berlin, 1990.Google Scholar
Ionescu-Tulcea, C. and Marinescu, G.. Théorie ergodique pour des classe d’opérarions non complètement continues. Ann. of Math. (2) 52 (1950), 140–147.Google Scholar
Jiang, M.. Differentiating potential functions of SRB measures on hyperbolic attractors. Ergod. Th. & Dynam. Sys. 32(4) (2012), 1350–1369.Google Scholar
Keller, G. and Liverani, C.. Stability of the spectrum for transfer operators. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 19 (1999), 141–152.Google Scholar
Krzyzewski, K.. Some results on expanding mappings. Asterisque 50 (1977), 205–218.Google Scholar
Liu, P., Qian, M. and Zhao, Y.. Large deviations in Axiom A endomorphisms. Proc. Roy. Soc. Edinburgh Sect. A 133A(6) (2003), 1379–1388.Google Scholar
Mañé, R. and Pugh, C.. Stability of endomorphisms. Dynamical Systems - Warwick 1974 (Lecture Notes in Mathematics, 468). Ed. Manning, A.. Springer, Berlin, 1975.Google Scholar
Mihailescu, E.. Unstable manifolds and Holder structures associated with noninvertible maps. Discrete Contin. Dyn. Syst. 14(3) (2006), 419–446.Google Scholar
Mihailescu, E.. Approximations of Gibbs states of arbitrary Holder potentials on hyperbolic folded sets. Discrete Contin. Dyn. Syst. 32(3) (2012), 961–975.Google Scholar
Mihailescu, E.. On some coding and mixing properties for a class of chaotic systems. Monatsh. Math. 167 (2012), 241–255.CrossRefGoogle Scholar
Mihailescu, E. and Urbański, M.. Entropy production for a class of inverse SRB measures. J. Stat. Phys. 150 (2013), 881–888.Google Scholar
Mihailescu, E. and Urbansky, M.. Inverse topological pressure with applications to holomorphic dynamics of several complex variables. Commun. Contemp. Math. 6(4) (2004), 653–679.Google Scholar
Mihailescu, E. and Urbansky, M.. Inverse pressure estimates and the independence of stable dimension for non-invertible maps. Canad. J. Math. 60 (2008), 658–684.Google Scholar
Pesin, Y.. Dimension Theory in Dynamical Systems (Contemporary Views and Applications). University of Chicago Press, Chicago, 1997.CrossRefGoogle Scholar
Pesin, Y. and Sinai, Y.. Gibbs measures for partially hyperbolic attractors. Ergod. Th. & Dynam. Sys. 2 (1982), 417–438.Google Scholar
Przytycki, F.. Anosov endomorphisms. Studia Math. 58(3) (1976), 249–285.Google Scholar
Przytycki, F.. On $\varOmega$ -stability and structural stability of endomorphisms satisfying Axiom A. Studia Math. 60 (1977), 61–77.CrossRefGoogle Scholar
Przytycki, F. and Urbanski, M.. Conformal Fractals: Ergodic Theory Methods. Cambridge University Press, Cambridge, 2010.CrossRefGoogle Scholar
Pugh, C. and Shub, M.. Ergodic attractors. Trans. Amer. Math. Soc. 312(1) (1989), 1–54.Google Scholar
Qian, M. and Xie, J.-S.. Smooth Ergodic Theory for Endomorphisms. Springer Verlag, Berlin, 2009.Google Scholar
Qian, M. and Zhang, Z.. Ergodic theory for Axiom A endomorphisms. Ergod. Th. & Dynam. Sys. 15 (1995), 161–174.CrossRefGoogle Scholar
Ruelle, D.. A measure associated with Axiom A attractors. Amer. J. Math. 98 (1976), 619–654.Google Scholar
Ruelle, D.. The thermodynamic formalism for expanding maps. Comm. Math. Phys. 125 (1989), 239–262.Google Scholar
Ruelle, D.. Differentiation of SRB states. Comm. Math. Phys. 187 (1997), 227–241.Google Scholar
Ruelle, D.. A review of linear response theory for general differentiable dynamical systems. Nonlinearity 22 (2009), 855–870.Google Scholar
Sacksteder, R.. The Measures Invariant Under an Expanding Map (Lecture Notes in Mathematics, 392). Springer, Berlin, 1974.Google Scholar
Sarig, O.. Introduction to the transfer operator method. Winter School on Dynamics. Hausdorff Research Institute for Mathematics, Bonn, 2020.Google Scholar
Shub, M.. Endomorphisms of compact differentiable manifolds. Amer. J. Math. 91(1) (1969), 175–199.Google Scholar
Simon, K.. The Hausdorff dimension of the Smale–Williams solenoid with different contraction coefficients. Proc. Amer. Math. Soc. 125(4) (1997), 1221–1228.CrossRefGoogle Scholar
Simon, K. and Solomyak, B.. Hausdorff dimension for horseshoes in R3 . Ergod. Th. & Dynam. Sys. 19(5) (1999), 1343–1363.CrossRefGoogle Scholar
Sinai, Y.. Gibbs measure in ergodic theory. Russian Math. Surveys 27 (1972), 21–69.Google Scholar
Tsujii, M.. Fat solenoidal attractors. Nonlinearity 14 (2001), 1011–1027.Google Scholar
Tsujii, M.. Physical measures for partially hyperbolic surface endomorphisms. Acta Math. 194 (2005), 37–132.Google Scholar
Urbansky, M. and Wolf, C.. SRB measures for Axiom A endomorphisms. Math. Res. Lett. 11(5–6) (2004), 785–797.Google Scholar
Zhang, Z.. On the smooth dependence of SRB measures for partially hyperbolic systems. Comm. Math. Phys. 358(1) (2018), 45–79.Google Scholar