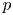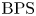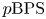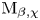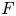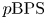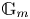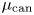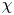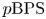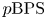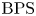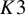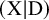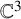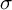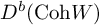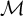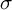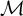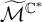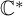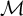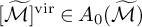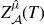115 results in 14Nxx
DT INVARIANTS FROM VERTEX ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 20 September 2024, pp. 1-49
-
- Article
-
- You have access
- HTML
- Export citation
Tropical curves in abelian surfaces I: enumeration of curves passing through points
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 19 September 2024, pp. 1-40
-
- Article
-
- You have access
- HTML
- Export citation
Flags of sheaves, quivers and symmetric polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 September 2024, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BPS invariants from p-adic integrals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1525-1550
- Print publication:
- July 2024
-
- Article
-
- You have access
- HTML
- Export citation
Quasimaps to moduli spaces of sheaves on a
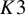 $K3$ surface
$K3$ surface
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 17 May 2024, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Logarithmic Donaldson–Thomas theory
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 April 2024, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on quantum K-theory of root constructions
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Virasoro Constraints for Toric Bundles
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 01 January 2024, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Categorical and K-theoretic Donaldson–Thomas theory of
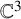 $\mathbb {C}^3$ (part II)
$\mathbb {C}^3$ (part II)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 December 2023, e108
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stellahedral geometry of matroids
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 09 October 2023, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Avoidance loci and tropicalizations of real bitangents to plane quartics
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 26 July 2023, pp. 1308-1312
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On weighted-blowup formulae of genus zero orbifold Gromov–Witten invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 19 July 2023, pp. 1833-1871
- Print publication:
- September 2023
-
- Article
-
- You have access
- HTML
- Export citation
Floor diagrams and enumerative invariants of line bundles over an elliptic curve
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 07 July 2023, pp. 1741-1790
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TANGENT-FILLING PLANE CURVES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 02 May 2023, pp. 301-315
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
INTRINSIC STABILIZER REDUCTION AND GENERALIZED DONALDSON–THOMAS INVARIANTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 02 May 2023, pp. 1987-2025
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equations of mirrors to log Calabi–Yau pairs via the heart of canonical wall structures
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 381-421
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Log Product Formula in Quantum K-theory
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 225-252
- Print publication:
- September 2023
-
- Article
-
- You have access
- HTML
- Export citation
Wonderful compactifications and rational curves with cyclic action
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 11 April 2023, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extremal Gromov-Witten invariants of the Hilbert scheme of
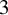 $3$
Points
$3$
Points
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 24 March 2023, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Motivic zeta functions of hyperplane arrangements
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 1 / July 2023
- Published online by Cambridge University Press:
- 07 March 2023, pp. 187-215
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation