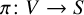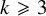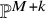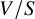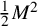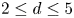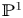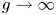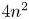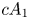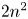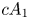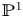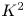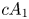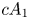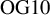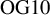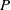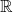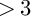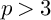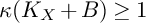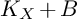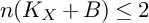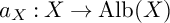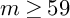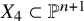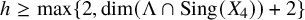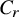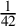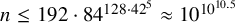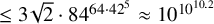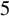185 results in 14Exx
Birationally rigid Fano-Mori fibre spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 21 October 2024, e84
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the embedded Nash problem
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 16 October 2024, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounding geometrically integral del Pezzo surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 14 October 2024, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIRATIONAL GEOMETRY OF SEXTIC DOUBLE SOLIDS WITH A COMPOUND
 $A_n$ SINGULARITY
$A_n$ SINGULARITY
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-52
-
- Article
-
- You have access
- HTML
- Export citation
Low-degree Hurwitz stacks in the Grothendieck ring
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1784-1849
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
2 n2-inequality for cA1 points and applications to birational rigidity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 29 May 2024, pp. 1551-1595
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONSTANCY OF THE HILBERT–SAMUEL FUNCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1-15
-
- Article
-
- You have access
- HTML
- Export citation
O’Grady tenfolds as moduli spaces of sheaves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 May 2024, e60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KOBAYASHI-OCHIAI’S FINITENESS THEOREM FOR ORBIFOLD PAIRS OF GENERAL TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Galois points and Cremona transformations
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A bound of the number of weighted blow-ups to compute the minimal log discrepancy for smooth 3-folds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 08 March 2024, pp. 495-515
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nef cones of fiber products and an application to the cone conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 05 March 2024, e28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NOTE ON THE THREE-DIMENSIONAL LOG CANONICAL ABUNDANCE IN CHARACTERISTIC
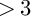 $>3$
$>3$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 28 February 2024, pp. 694-723
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Minimal log discrepancies of hypersurface mirrors
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 19 February 2024, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hensel minimality II: Mixed characteristic and a diophantine application
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 October 2023, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE ANTI-CANONICAL GEOMETRY OF WEAK
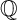 $\mathbb {Q}$-FANO THREEFOLDS, III
$\mathbb {Q}$-FANO THREEFOLDS, III
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 23-47
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
Nonsolidity of uniruled varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 15 August 2023, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quartic and Quintic Hypersurfaces with Dense Rational Points
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 June 2023, e55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Remark on complements on surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 26 May 2023, e42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Angehrn-Siu-Helmke’s method applied to abelian varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 11 May 2023, e38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation