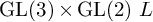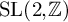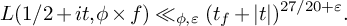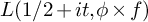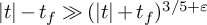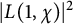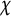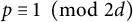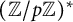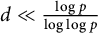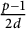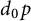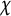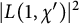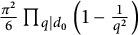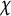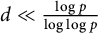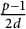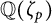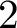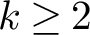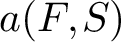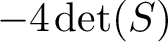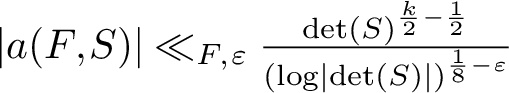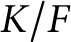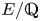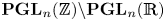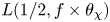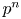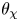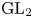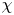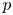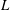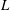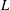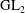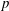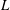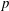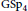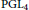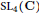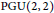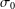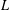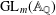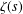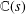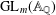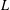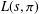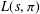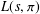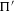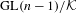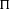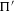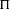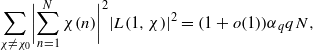25 results
UNIFORM BOUNDS FOR
 $\operatorname {GL}(3)\times \operatorname {GL}(2)$ L-FUNCTIONS
$\operatorname {GL}(3)\times \operatorname {GL}(2)$ L-FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 17 October 2023, pp. 1-44
-
- Article
- Export citation
SHORT CHARACTER SUMS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 11 July 2023, pp. 339-340
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
The error term in the truncated Perron formula for the logarithm of an L-function
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 09 March 2023, pp. 1122-1134
- Print publication:
- December 2023
-
- Article
- Export citation
Mean square values of L-functions over subgroups for nonprimitive characters, Dedekind sums and bounds on relative class numbers
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 30 January 2023, pp. 1711-1743
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON FUNDAMENTAL FOURIER COEFFICIENTS OF SIEGEL CUSP FORMS OF DEGREE 2
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 12 November 2021, pp. 1819-1869
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A proof of the linear Arithmetic Fundamental Lemma for
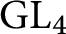 $ \operatorname {{\mathrm {GL}}}_4$
$ \operatorname {{\mathrm {GL}}}_4$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 23 November 2020, pp. 381-427
- Print publication:
- April 2022
-
- Article
- Export citation
Non-vanishing of class group L-functions for number fields with a small regulator
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 17 December 2020, pp. 2423-2436
- Print publication:
- November 2020
-
- Article
- Export citation
Sup-norms of eigenfunctions in the level aspect for compact arithmetic surfaces, II: newforms and subconvexity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 15 December 2020, pp. 2368-2398
- Print publication:
- November 2020
-
- Article
- Export citation
Weighted Distribution of Low-lying Zeros of GL(2)
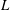 $L$-functions
$L$-functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 08 January 2019, pp. 153-182
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
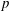 $p$-adic
$p$-adic 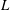 $L$-functions for
$L$-functions for 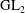 $\text{GL}_{2}$
$\text{GL}_{2}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1019-1059
- Print publication:
- October 2019
-
- Article
- Export citation
One Level Density for Cubic Galois Number Fields
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 149-167
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
Multivariate Rankin–Selberg Integrals on GL4 and GU(2, 2)
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 4 / 01 December 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 822-835
- Print publication:
- 01 December 2018
-
- Article
-
- You have access
- Export citation
ON ALGEBRAIC DIFFERENTIAL EQUATIONS FOR THE GAMMA FUNCTION AND
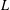 $L$-FUNCTIONS IN THE EXTENDED SELBERG CLASS
$L$-FUNCTIONS IN THE EXTENDED SELBERG CLASS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 36-43
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
A Simple Proof and Strengthening of a Uniqueness Theorem for L-functions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 1 / 01 March 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 119-122
- Print publication:
- 01 March 2016
-
- Article
-
- You have access
- Export citation
HYPERTRANSCENDENCE OF
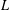 $L$-FUNCTIONS FOR
$L$-FUNCTIONS FOR 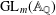 $\text{GL}_{m}(\mathbb{A}_{\mathbb{Q}})$
$\text{GL}_{m}(\mathbb{A}_{\mathbb{Q}})$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 388-399
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
WHITTAKER PERIODS, MOTIVIC PERIODS, AND SPECIAL VALUES OF TENSOR PRODUCT
 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 31 March 2015, pp. 711-769
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
UNIQUENESS THEOREMS FOR DIRICHLET SERIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 12 February 2015, pp. 389-399
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
On Complex Explicit Formulae Connected with the Möbius Function of an Elliptic Curve
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 2 / 14 June 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 381-389
- Print publication:
- 14 June 2014
-
- Article
-
- You have access
- Export citation
A Candidate for the Abelian Category of Mixed Elliptic Motives
-
- Journal:
- Journal of K-Theory / Volume 12 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 15 November 2013, pp. 569-600
- Print publication:
- December 2013
-
- Article
- Export citation
ON SOME WEIGHTED AVERAGE VALUES OF L-FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 26 February 2009, pp. 183-186
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation