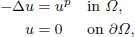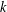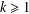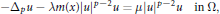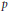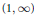19 results
Generalized second order vectorial ∞-eigenvalue problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 March 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On generalized eigenvalue problems of fractional (p, q)-Laplace operator with two parameters
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 January 2024, pp. 1-46
-
- Article
-
- You have access
- HTML
- Export citation
On the policy improvement algorithm for ergodic risk-sensitive control
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 02 September 2020, pp. 1305-1330
- Print publication:
- August 2021
-
- Article
- Export citation
The spectrum of the mean curvature operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 01 April 2020, pp. 451-463
- Print publication:
- April 2021
-
- Article
- Export citation
Generalized eigenvalues of the (P, 2)-Laplacian under a parametric boundary condition
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 December 2019, pp. 287-303
-
- Article
- Export citation
Bifurcation of nonlinear bound states in the periodic Gross-Pitaevskii equation with 𝒫𝒯-symmetry
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 24 January 2019, pp. 171-204
- Print publication:
- February 2020
-
- Article
- Export citation
Bifurcation and standing wave solutions for a quasilinear Schrödinger equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 939-968
- Print publication:
- August 2019
-
- Article
- Export citation
Normalized solutions for nonlinear Schrödinger systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 20 November 2017, pp. 225-242
- Print publication:
- April 2018
-
- Article
- Export citation
A short remark regarding Pohozaev-type results on general domains assuming finite Morse index
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 16 January 2017, pp. 293-297
- Print publication:
- April 2017
-
- Article
- Export citation
Pseudo-Arclength Continuation Algorithms for Binary Rydberg-Dressed Bose-Einstein Condensates
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 12 April 2016, pp. 1067-1093
- Print publication:
- April 2016
-
- Article
- Export citation
An Adaptive Finite Element Method with Hybrid Basis for Singularly Perturbed Nonlinear Eigenvalue Problems
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 01 February 2016, pp. 442-472
- Print publication:
- February 2016
-
- Article
- Export citation
EIGENVALUE HOMOGENISATION PROBLEM WITH INDEFINITE WEIGHTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 15 October 2015, pp. 113-127
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
Error Estimates of Some Numerical Atomic Orbitals in Molecular Simulations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 1 / July 2015
- Published online by Cambridge University Press:
- 03 July 2015, pp. 125-146
- Print publication:
- July 2015
-
- Article
- Export citation
THE DEPENDENCE OF THE FIRST EIGENVALUE OF THE INFINITY LAPLACIAN WITH RESPECT TO THE DOMAIN
-
- Journal:
- Glasgow Mathematical Journal / Volume 56 / Issue 2 / May 2014
- Published online by Cambridge University Press:
- 02 September 2013, pp. 241-249
- Print publication:
- May 2014
-
- Article
-
- You have access
- Export citation
A Two-Parameter Continuation Method for Rotating Two-Component Bose-Einstein Condensates in Optical Lattices
-
- Journal:
- Communications in Computational Physics / Volume 13 / Issue 2 / February 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 442-460
- Print publication:
- February 2013
-
- Article
- Export citation
A Novel Perturbative Iteration Algorithm for Effective and Efficient Solution of Frequency-Dependent Eigenvalue Problems
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 4 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 03 June 2015, pp. 325-339
- Print publication:
- June 2012
-
- Article
- Export citation
Multiple Solutions for a Class of Neumann Elliptic Problems on Compact Riemannian Manifolds with Boundary
-
- Journal:
- Canadian Mathematical Bulletin / Volume 53 / Issue 4 / 01 December 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 674-683
- Print publication:
- 01 December 2010
-
- Article
-
- You have access
- Export citation
On the Principal Eigencurve of the p-Laplacian: Stability Phenomena
-
- Journal:
- Canadian Mathematical Bulletin / Volume 49 / Issue 3 / 01 September 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 358-370
- Print publication:
- 01 September 2006
-
- Article
-
- You have access
- Export citation
Points of Spherical Maxima and Solvability of Semilinear Elliptic Equations
-
- Journal:
- Canadian Journal of Mathematics / Volume 43 / Issue 4 / 01 August 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 825-831
- Print publication:
- 01 August 1991
-
- Article
-
- You have access
- Export citation

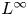
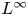
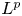
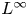
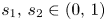
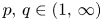
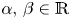
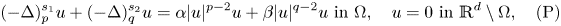
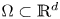
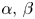
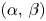
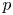
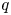
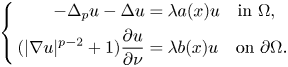
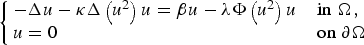
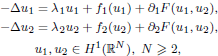
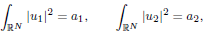
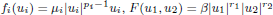 , with positive constants
, with positive constants 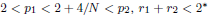 in dimensions 2 ≤
in dimensions 2 ≤