13 results
Central extensions and rational quadratic forms
-
- Journal:
- Nagoya Mathematical Journal / Volume 130 / June 1993
- Published online by Cambridge University Press:
- 22 January 2016, pp. 177-182
- Print publication:
- June 1993
-
- Article
-
- You have access
- Export citation
Gauss’s ternary form reduction and its application to a prime decomposition symbol
-
- Journal:
- Nagoya Mathematical Journal / Volume 98 / June 1985
- Published online by Cambridge University Press:
- 22 January 2016, pp. 77-86
- Print publication:
- June 1985
-
- Article
-
- You have access
- Export citation
A norm residue map for central extensions of an algebraic number field
-
- Journal:
- Nagoya Mathematical Journal / Volume 93 / March 1984
- Published online by Cambridge University Press:
- 22 January 2016, pp. 61-69
- Print publication:
- March 1984
-
- Article
-
- You have access
- Export citation
A prime decomposition symbol for a non-abelian central extension which is abelian over a bicyclic biquadratic field
-
- Journal:
- Nagoya Mathematical Journal / Volume 79 / October 1980
- Published online by Cambridge University Press:
- 22 January 2016, pp. 79-109
- Print publication:
- October 1980
-
- Article
-
- You have access
- Export citation
Note on class number factors and prime decompositions
-
- Journal:
- Nagoya Mathematical Journal / Volume 66 / May 1977
- Published online by Cambridge University Press:
- 22 January 2016, pp. 167-182
- Print publication:
- May 1977
-
- Article
-
- You have access
- Export citation
On nilpotent factors of congruent ideal class groups of Galois extensions
-
- Journal:
- Nagoya Mathematical Journal / Volume 62 / September 1976
- Published online by Cambridge University Press:
- 22 January 2016, pp. 13-28
- Print publication:
- September 1976
-
- Article
-
- You have access
- Export citation
On Class Field Towers and the Rank of Ideal Class Groups
-
- Journal:
- Nagoya Mathematical Journal / Volume 48 / December 1972
- Published online by Cambridge University Press:
- 22 January 2016, pp. 147-157
- Print publication:
- December 1972
-
- Article
-
- You have access
- Export citation
Über das Geschlecht und Die Klassenzahl Eines Relativ-Galoischen Zahlkörpers vom Primzahlpotenzgrade
-
- Journal:
- Nagoya Mathematical Journal / Volume 37 / March 1970
- Published online by Cambridge University Press:
- 22 January 2016, pp. 197-200
- Print publication:
- March 1970
-
- Article
-
- You have access
- Export citation
On the Galois Cohomology Group of the Ring of Integers in a Global Field and its Adele Ring
-
- Journal:
- Nagoya Mathematical Journal / Volume 32 / June 1968
- Published online by Cambridge University Press:
- 22 January 2016, pp. 247-252
- Print publication:
- June 1968
-
- Article
-
- You have access
- Export citation
The Genus Field and Genus Number in Algebraic Number Fields
-
- Journal:
- Nagoya Mathematical Journal / Volume 29 / March 1967
- Published online by Cambridge University Press:
- 22 January 2016, pp. 281-285
- Print publication:
- March 1967
-
- Article
-
- You have access
- Export citation
The Notion of Restricted Idèles with Application to Some Extension Fields
-
- Journal:
- Nagoya Mathematical Journal / Volume 27 / Issue 1 / February 1966
- Published online by Cambridge University Press:
- 22 January 2016, pp. 121-132
- Print publication:
- February 1966
-
- Article
-
- You have access
- Export citation
A Property of Meta-Abelian Extensions
-
- Journal:
- Nagoya Mathematical Journal / Volume 19 / October 1961
- Published online by Cambridge University Press:
- 22 January 2016, pp. 169-187
- Print publication:
- October 1961
-
- Article
-
- You have access
- Export citation
On Meta Abelian Fields of a Certain Type
-
- Journal:
- Nagoya Mathematical Journal / Volume 14 / February 1959
- Published online by Cambridge University Press:
- 22 January 2016, pp. 193-199
- Print publication:
- February 1959
-
- Article
-
- You have access
- Export citation



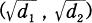 be a bicyclic biquadratic field, and let
be a bicyclic biquadratic field, and let 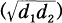 . Denote by
. Denote by 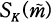 the ray class field mod
the ray class field mod 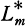 be the maximal abelian extension over Q contained in
be the maximal abelian extension over Q contained in 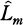 be the maximal extension contained in
be the maximal extension contained in 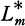 /Q if and only if
/Q if and only if 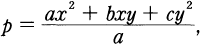
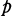 is decomposed completely in
is decomposed completely in 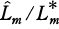 if and only if
if and only if 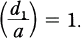 .
.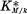 resp.
resp. 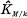 the genus field resp. the central class field of
the genus field resp. the central class field of 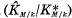 is isomorphic to a factor group of the Schur multiplicator
is isomorphic to a factor group of the Schur multiplicator 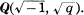 In the present paper we study on the case over a biquadratic field
In the present paper we study on the case over a biquadratic field 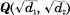 in general. We define a symbol [
in general. We define a symbol [ be a congruent ideal class group of
be a congruent ideal class group of 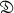 of
of 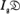 is the group of all elements
is the group of all elements 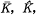 bzw.
bzw. 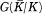 abelsch; die galoische Gruppe
abelsch; die galoische Gruppe 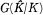 ist im Zentrum von
ist im Zentrum von 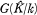 enthalten;
enthalten; 