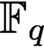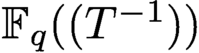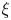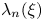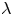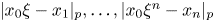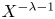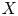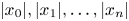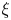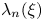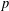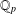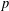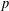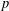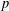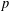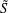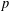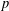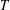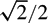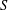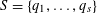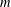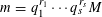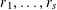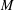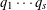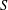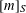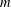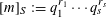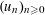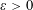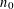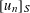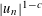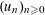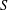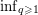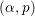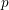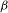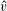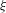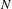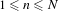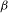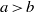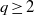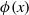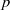80 results
MAHLER’S AND KOKSMA’S CLASSIFICATIONS IN FIELDS OF POWER SERIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 246 / June 2022
- Published online by Cambridge University Press:
- 07 June 2021, pp. 355-371
- Print publication:
- June 2022
-
- Article
- Export citation
On simultaneous rational approximation to a p-adic number and its integral powers, II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 07 May 2021, pp. 317-337
-
- Article
- Export citation
ON SPRINDŽUK’S CLASSIFICATION OF
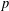 $p$-ADIC NUMBERS
$p$-ADIC NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 12 December 2019, pp. 221-231
- Print publication:
- October 2021
-
- Article
- Export citation
Metrical Results on the Distribution of Fractional Parts of Powers of Real Numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 505-521
-
- Article
- Export citation
ON MAHLER’S CLASSIFICATION OF
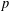 $p$-ADIC NUMBERS
$p$-ADIC NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 30 July 2018, pp. 203-211
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
Hausdorff dimension and uniform exponents in dimension two
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 167 / Issue 2 / September 2019
- Published online by Cambridge University Press:
- 29 May 2018, pp. 249-284
- Print publication:
- September 2019
-
- Article
- Export citation
On the digital representation of smooth numbers
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 165 / Issue 3 / November 2018
- Published online by Cambridge University Press:
- 29 August 2017, pp. 533-540
- Print publication:
- November 2018
-
- Article
- Export citation
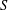 $S$-PARTS OF TERMS OF INTEGER LINEAR RECURRENCE SEQUENCES
$S$-PARTS OF TERMS OF INTEGER LINEAR RECURRENCE SEQUENCES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 840-851
- Print publication:
- 2017
-
- Article
- Export citation
ON THE EXPANSIONS OF REAL NUMBERS IN TWO MULTIPLICATIVELY DEPENDENT BASES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 01 December 2016, pp. 373-383
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
2 - Exponents of Diophantine Approximation
-
-
- Book:
- Dynamics and Analytic Number Theory
- Published online:
- 03 November 2016
- Print publication:
- 10 November 2016, pp 96-135
-
- Chapter
- Export citation
Effective irrationality measures for real and p-adic roots of rational numbers close to 1, with an application to parametric families of Thue–Mahler equations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 164 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 27 September 2016, pp. 99-108
- Print publication:
- January 2018
-
- Article
- Export citation
On the complexity of a putative counterexample to the
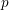 $p$-adic Littlewood conjecture
$p$-adic Littlewood conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 9 / September 2015
- Published online by Cambridge University Press:
- 19 May 2015, pp. 1647-1662
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
Uniform Diophantine approximation related to
 $b$-ary and
$b$-ary and 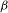 ${\it\beta}$-expansions
${\it\beta}$-expansions
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 36 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 04 August 2014, pp. 1-22
- Print publication:
- February 2016
-
- Article
- Export citation
PERFECT POWERS WITH THREE DIGITS
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 06 August 2013, pp. 66-84
- Print publication:
- January 2014
-
- Article
- Export citation
Perfect powers with few binary digits and related Diophantine problems, II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 153 / Issue 3 / November 2012
- Published online by Cambridge University Press:
- 16 August 2012, pp. 525-540
- Print publication:
- November 2012
-
- Article
- Export citation
5 - Further explicit constructions of normal and non-normal numbers
-
- Book:
- Distribution Modulo One and Diophantine Approximation
- Published online:
- 05 October 2012
- Print publication:
- 05 July 2012, pp 102-117
-
- Chapter
- Export citation
Appendix D - Continued fractions
-
- Book:
- Distribution Modulo One and Diophantine Approximation
- Published online:
- 05 October 2012
- Print publication:
- 05 July 2012, pp 241-245
-
- Chapter
- Export citation
Preface
-
- Book:
- Distribution Modulo One and Diophantine Approximation
- Published online:
- 05 October 2012
- Print publication:
- 05 July 2012, pp ix-xiv
-
- Chapter
- Export citation
9 - Continued fraction expansions and β-expansions
-
- Book:
- Distribution Modulo One and Diophantine Approximation
- Published online:
- 05 October 2012
- Print publication:
- 05 July 2012, pp 195-213
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Distribution Modulo One and Diophantine Approximation
- Published online:
- 05 October 2012
- Print publication:
- 05 July 2012, pp i-iv
-
- Chapter
- Export citation