Hostname: page-component-848d4c4894-2xdlg Total loading time: 0 Render date: 2024-06-26T21:23:27.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Hausdorff dimension and uniform exponents in dimension two

Published online by Cambridge University Press:  29 May 2018

YANN BUGEAUD ,
YITWAH CHEUNG  and
NICOLAS CHEVALLIER
YANN BUGEAUD
Affiliation:
IRMA, U.M.R. 7501, Université de Strasbourg et C.N.R.S. 7 rue René Descartes, 67084 Strasbourg, France. e-mail: bugeaud@math.unistra.fr
YITWAH CHEUNG
Affiliation:
San Francisco State University, 1600 Holloway Ave, San Francisco, CA 94132, U.S.A. e-mail: ycheung@sfsu.edu
NICOLAS CHEVALLIER
Affiliation:
Haute Alsace University, 4 Rue des Frères Lumière, 68093 Mulhouse Cedex, France. e-mail: nicolas.chevallier@uha.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we prove that the Hausdorff dimension of the set of (nondegenerate) singular two-dimensional vectors with uniform exponent μ in (1/2, 1) is equal to 2(1 − μ) for μ ⩾ 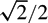$\sqrt2/2$, whereas for μ < 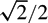$\sqrt2/2$ it is greater than 2(1 − μ) and at most equal to (3 − 2 μ)(1 − μ)/(1 − μ + μ2). We also establish that this dimension tends to 4/3 (which is the dimension of the set of singular two-dimensional vectors) when μ tends to 1/2. These results improve upon previous estimates of R. Baker, joint work of the first author with M. Laurent, and unpublished work of M. Laurent. Moreover, we prove a lower bound for the packing dimension, which appears to be strictly greater than the Hausdorff dimension for μ ⩾ 0.565. . . .

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 167 , Issue 2 , September 2019 , pp. 249 - 284
Copyright
Copyright © Cambridge Philosophical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Partially supported by NSF Grant DMS 1600476.

References

REFERENCES

[1] Baker, R. C. Singular n-tuples and Hausdorff dimension. Math. Proc. Camb. Phil. Soc. 81 (1977), 377–385.Google Scholar
[2] Baker, R. C. Singular n-tuples and Hausdorff dimension, II. Math. Proc. Camb. Phil. Soc. 111 (1992), 577–584.Google Scholar
[3] Bernik, V. I. and Dodson, M. M. Metric Diophantine approximation on manifolds. Cambridge Tracts in Mathematics 137 (Cambridge University Press, 1999.)Google Scholar
[4] Bugeaud, Y. Approximation by algebraic numbers. Cambridge Tracts in Mathematics (Cambridge, 2004).Google Scholar
[5] Bugeaud, Y. Exponents of Diophantine approximation. In: Dynamics and Analytic Number Theory. Proceedings of the Durham Easter School (2014). Edited by Badziahin, D., Gorodnik, A., Peyerimhoff, N. (Cambridge University Press). To appear.Google Scholar
[6] Bugeaud, Y. and Laurent, M. Exponents of Diophantine approximation and Sturmian continued fractions. Ann. Inst. Fourier 55 (2005), 773–804.Google Scholar
[7] Bugeaud, Y. and Laurent, M. Exponents of homogeneous and inhomogeneous Diophantine approximation. Moscow Math. J. 5 (2005), 747–766.Google Scholar
[8] Cassels, J. W. S. An introduction to Diophantine approximation. Cambridge Tracts in Math. and Math. Phys., vol. 99 (Cambridge University Press, 1957).Google Scholar
[9] Cheung, Y. Hausdorff dimension of the set of points on divergent trajectories of a homogeneous flow on a product space. Ergodic Theory Dynam. Systems 27 (2007), 65–85.Google Scholar
[10] Cheung, Y. Hausdorff dimension of the set of singular pairs. Ann. of Math. 173 (2011), 127–167.Google Scholar
[11] Cheung, Y. and Chevallier, N. Hausdorff dimension of singular vectors. Duke Math. 165 (12) (2016), 2273–2329.Google Scholar
[12] Chevallier, N. Best simultaneous Diophantine approximations and multidimensional continued fraction expansions. Mosc. J. Comb. Number Theory 3 (2013), 3–56.Google Scholar
[13] Das, T., Fishman, L., Simmons, D. and M. Urbański. A variational principle in the parametric geometry of numbers, with application to metric Diophantine approximation. C. R. Math. Acad. Sci. Paris 355 (2017), no. 8, 835–846.Google Scholar
[14] Davenport, H. and Schmidt, W. M. Dirichlet's theorem on Diophantine approximation. Symposia Mathematica, Vol. IV (INDAM, Rome, 1968/69), pp. 113–132 (Academic Press, London, 1970).Google Scholar
[15] Davenport, H. and Schmidt, W. M. Dirichlet's theorem on Diophantine approximation. II. Acta Arith. 16 (1970), 413–423.Google Scholar
[16] Dodson, M. M. Hausdorff dimension, lower order and Khintchine's theorem in metric Diophantine approximation. J. Reine Angew. Math. 432 (1992), 69–76.Google Scholar
[17] Falconer, K. FRACTAL GEOMETRY Mathematical foundations and applications. (John Wiley and Sons 1997).Google Scholar
[18] Jarník, V.. V Zum Khintchineschen “Übertragungssatz”. Trav. Inst. Math. Tbilissi 3 (1938), 193–212.Google Scholar
[19] Jarn, V. Contribution la thorie des approximations diophantiennes linaires et homognes. Czechoslovak Math. J. 4 (79) (1954), 330–353 (Russian).Google Scholar
[20] Kadyrov, S., Kleinbock, D., Lindenstrauss, E. and Margulis, G. A. Singular systems of linear forms and non-escape of mass in the space of lattices. J. Anal. Math. 133 (2017), 253–277.Google Scholar
[21] Khintchine, A. Ya. Über eine Klasse linearer diophantischer Approximationen. Rendiconti Circ. Mat. Palermo 50 (1926), 170–195.Google Scholar
[22] Khintchine, A. Ya. Regular systems of linear equations and a general problem of Čebyšev. Izvestiya Akad. Nauk SSSR Ser. Mat. 12 (1948), 249–258.Google Scholar
[23] Kleinbock, D. and Weiss, B. Dirichlet's theorem on Diophantine approximation and homogeneous flows. J. Mod. Dyn. 2 (2008), 43–62.Google Scholar
[24] Lagarias, J. C. Best simultaneous Diophantine approximations. II. Behaviour of consecutive best approximations. Pacific J. Math. 102 (1982), 61–88.Google Scholar
[25] Lagarias, J. C. Some new results in simultaneous Diophantine approximation. Proc. Queens's University Number Theory Conference 1979 (Ribenboim, P., Ed.). Queen's Papers in Pure and Applied Math. No. 54 (Queen's University, 1980), 453–474.Google Scholar
[26] McMullen, C. T. Hausdorff Dimension and Conformal Dynamics, III: Computation of dimension. Amer. J. Math. 120, No. 4 (Aug., 1998), pp. 691–721.Google Scholar
[27] Moshchevitin, N. G. Best Diophantine approximations: the phenomenon of degenerate dimension. Surveys in geometry and number theory, reports on contemporary Russian mathematics. 158–182, London Math. Soc. Lecture Note Ser., 338 (Cambridge University Press, Cambridge, 2007).Google Scholar
[28] Roy, D. Approximation to real numbers by cubic algebraic integers I. Proc. London Math. Soc. 88 (2004), 42–62.Google Scholar
[29] Rynne, B. P. A lower bound for the Hausdorff dimension of sets of singular n-tuples. Math. Proc. Camb. Phil. Soc. 107 (1990), 387–394.Google Scholar
[30] Rynne, B. P. The Hausdorff dimension of certain sets of singular n-tuples. Math. Proc. Camb. Phil. Soc. 108 (1990), 105–110.Google Scholar
[31] Schmidt, W. M. Badly approximable systems of linear forms. J. Number Theory 1 (1969), 139–154.Google Scholar
[32] Shah, N. A. Equidistribution of expanding translates of curves and Dirichlet's theorem on Diophantine approximation. Invent. Math. 177 (2009), 509–532.Google Scholar
[33] Shah, N. A. Expanding translates of curves and Dirichlet–Minkowski theorem on linear forms. J. Amer. Math. Soc. 23 (2010), 563–589.Google Scholar
[34] Yavid, K. Y. An estimate for the Hausdorff dimension of sets of singular vectors. Dokl. Akad. Nauk BSSR 31 (1987), 777–780 (in Russian).Google Scholar